17. Comparer les images de deux nombres

Introduction

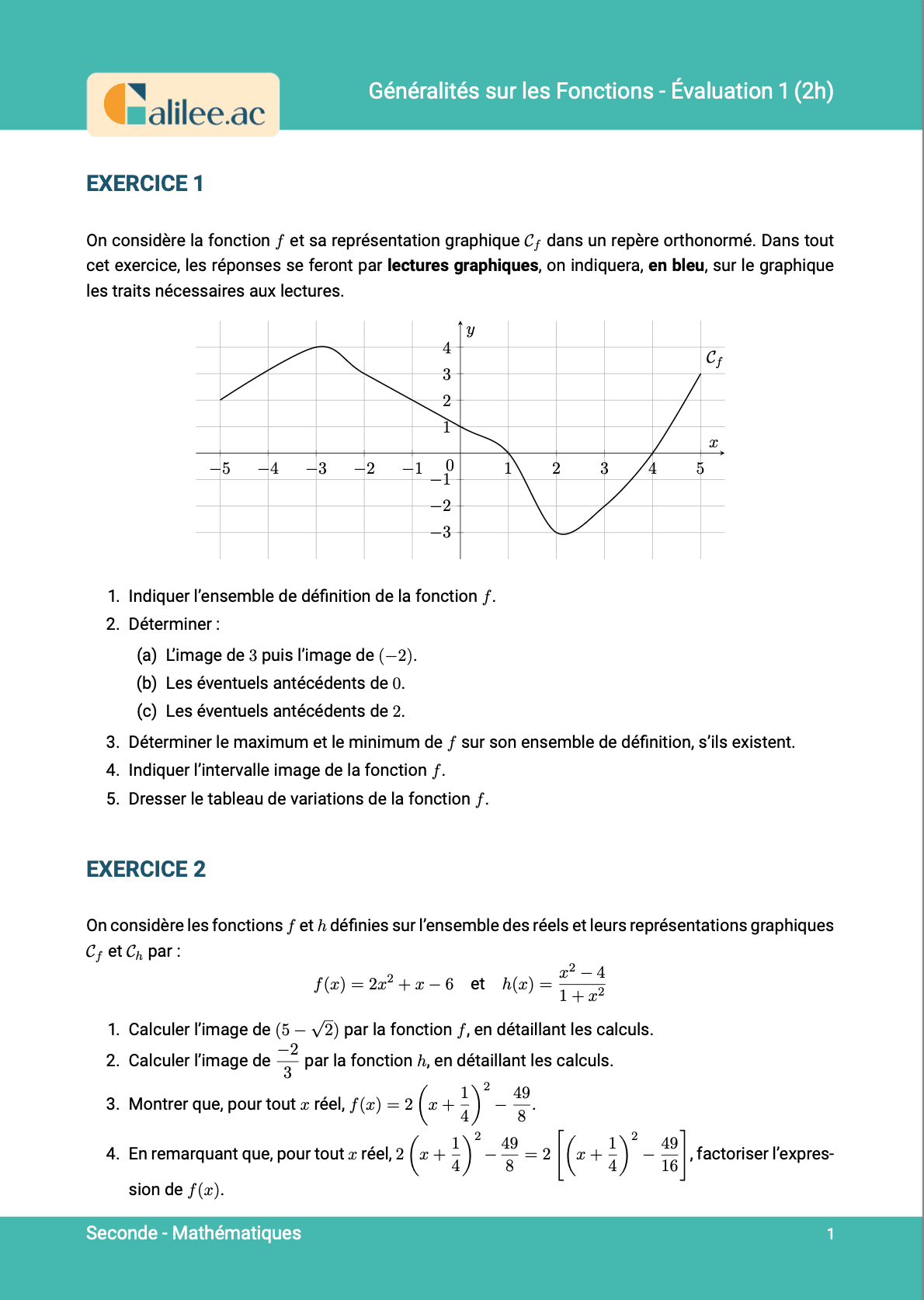
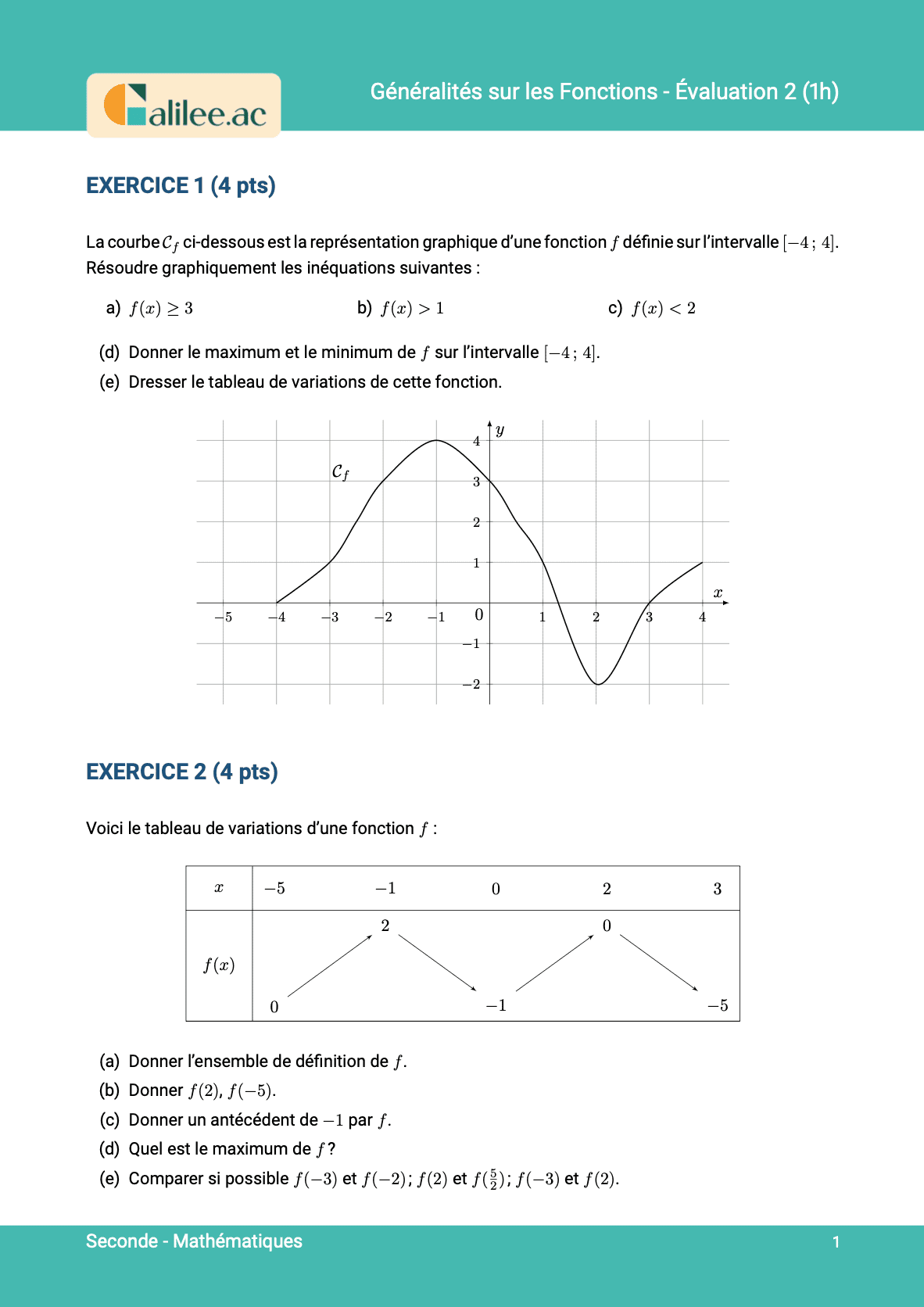
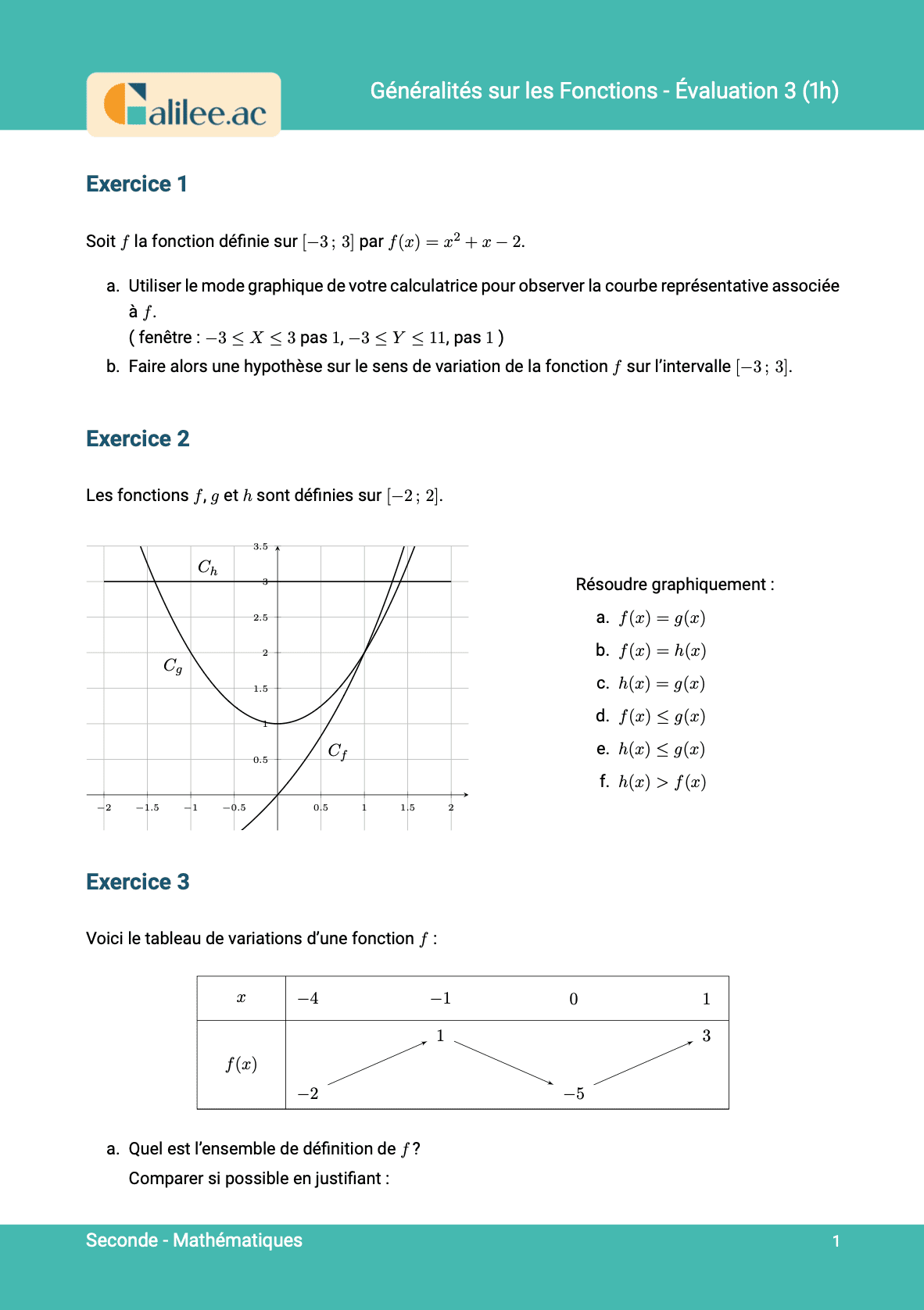
Allez les amis, on est parti pour voir comment faire pour comparer des images de nombres \(f(2) - 3\) et \(f(2) - 2\) sachant qu'on vous a donné seulement le tableau de variation de la fonction. On s'y met tout de suite. On va voir qu'il y a trois types de cas. Mes deux premières questions, ça correspond aux cas simples et les deux dernières aux cas compliqués.

Comparaison des images de nombres

Première chose à faire quand vous voulez comparer \(f(-3)\) et \(f(2) - 2\), c'est de déterminer lequel des deux, entre -3 et 2, et -2 est le plus petit. Donc on est dans le négatif, -3 est très négatif, -2 est négatif mais un peu moins. Du coup, on peut dire qu'on a \(f(-3)\) qui est strictement inférieur à \(f(-2)\). On a vu que quand la fonction était croissante, les images étaient dans le même ordre que les nombres. Donc si \(f(-3)\) est plus petit que \(f(-2)\) et que \(f\) est croissante, je peux dire que \(f(-3)\) est aussi plus petit que \(f(-2)\). Si \(f\) est décroissante, \(f(-3)\) sera plus grand que \(f(-2)\). Comment est-ce que je fais pour savoir ça ? Eh bien, je place -3 et -2 dans mon tableau. -3 est là, -2 est là. On voit que entre -3 et -2, la fonction est croissante. Vu que la fonction est croissante, l'ordre entre \(f(-3)\) et \(f(-2)\) ne va pas changer. Donc je peux dire que \(f(-3)\) sera aussi plus petit que \(f(-2)\).

Deuxième cas de figure

Pour le deuxième cas de figure, \(f(2) - 1\) et \(f(2) - 0\), je recommence, je les classe dans l'ordre. 0 est plus petit que 1. Ensuite, je vais regarder où ils sont dans le tableau. Ils sont tous les deux entre -1 et 2. Donc pour \(f(2) - 0\) et \(f(2) - 1\), la fonction est décroissante. Du coup, l'ordre entre \(f(2) - 0\) et \(f(2) - 1\) va changer. On va passer de plus petit à plus grand.

Cas compliqués

Voyons maintenant les cas compliqués. Pour \(f(2) - 0.5\) et \(f(2) - 1.5\), je vais les positionner. -1.5 est négatif, donc c'est plus petit que 0.5. Mais je regarde où ils sont sur mon tableau. -1.5 est là et 0.5 est là. Quand on est dans ce cas, entre -1.5 et 0.5, on se rend compte que la fonction est une fois croissante, une fois décroissante. Quand vous êtes dans ce cas de figure, c'est-à-dire entre les deux nombres, vous arrivez sur un sommet et la fonction est une fois croissante, une fois décroissante, vous ne pouvez tout simplement pas savoir quel est l'ordre des images.

Quatrième cas de figure

Pour le quatrième cas de figure, on se retrouve encore avec quelque chose comme ça. Donc on va positionner -3 et 3. Je sais que mon -3 est plus petit que mon 3. Je les fais apparaître sur le tableau. -3 est là, 3 est ici. Là, on a envie de dire que, vu qu'entre -3 et 3, la fonction est d'abord croissante puis décroissante, il n'y a aucun moyen de savoir comment seront les images l'une par rapport à l'autre. Sauf que, regardez, quand la fonction va de -4 à -1, c'est là qu'elle passe par \(f(2) - 3\) et elle monte jusqu'à 5. Donc \(f(2) - 3\) est positif. Pourquoi ? Parce que \(f(2) - 3\) va jusqu'à 5. Dans tous les cas, il va rester dans les nombres positifs. Pour \(f(2) - 3\), c'est entre 2 et 7 et entre 2 et 7, la fonction va de -4 à -2. Donc \(f(2) - 3\) est négatif. Sans même avoir besoin de réfléchir à cette histoire de croissance ou de décroissance, si vous avez \(f(2) - 3\) qui est positif et \(f(2) - 3\) qui est négatif, vous pouvez directement dire que celui qui est positif, donc \(f(2) - 3\), est plus grand que celui qui est négatif. On a vu les quatre cas de figure. Ce n'est pas évident, ce sont des exercices qui tombent au contrôle. Entraînez-vous et en appelant juste.