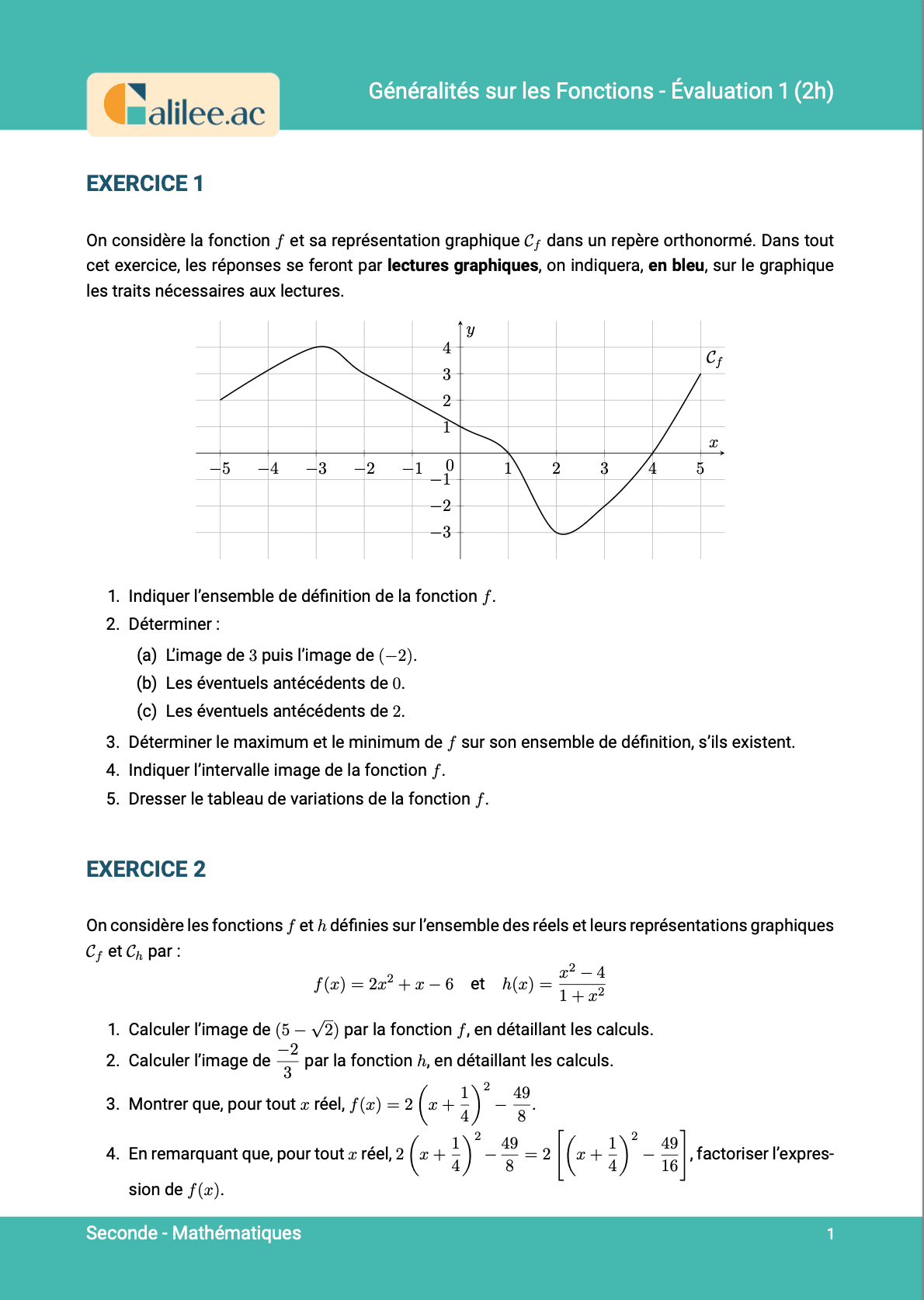
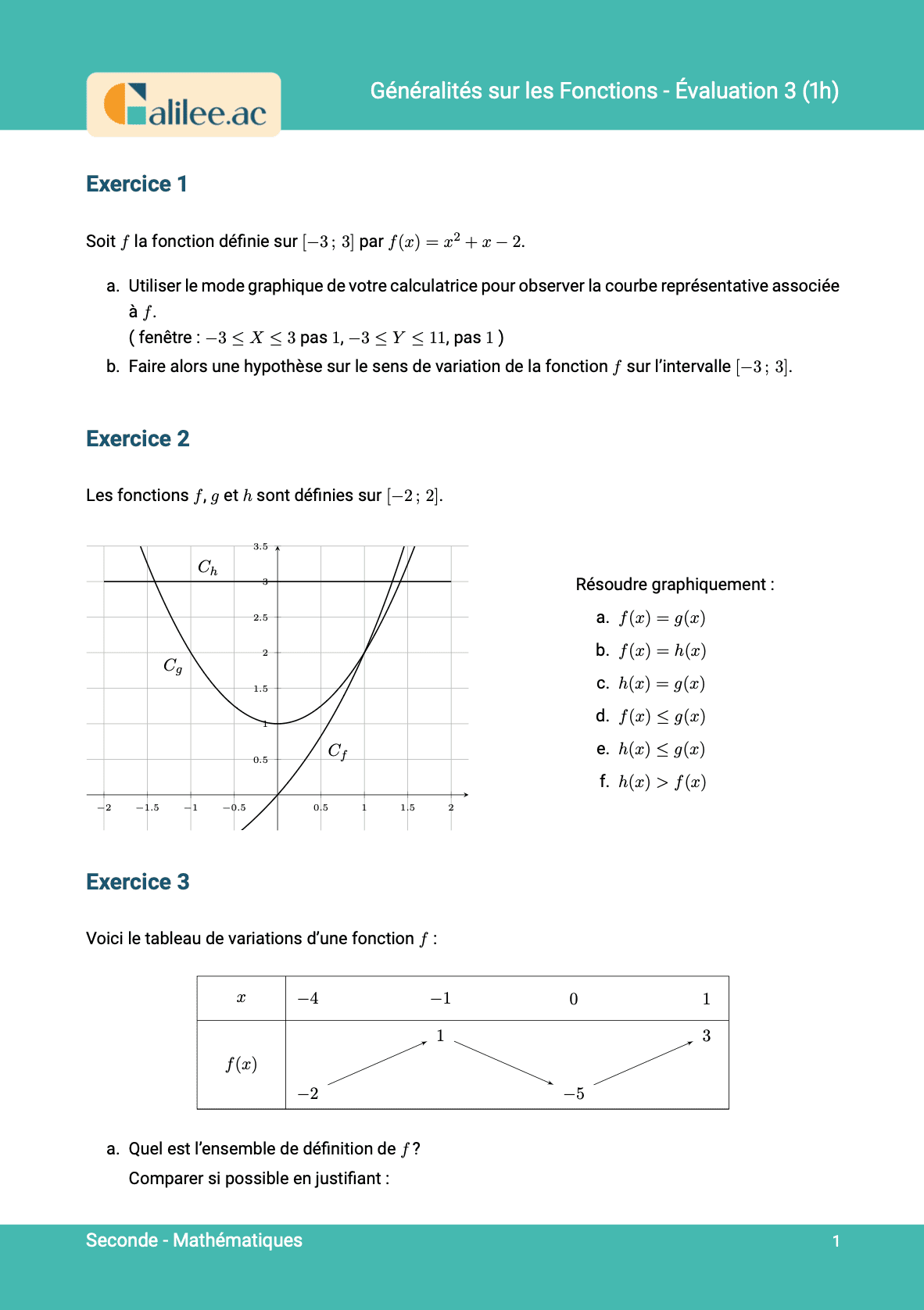
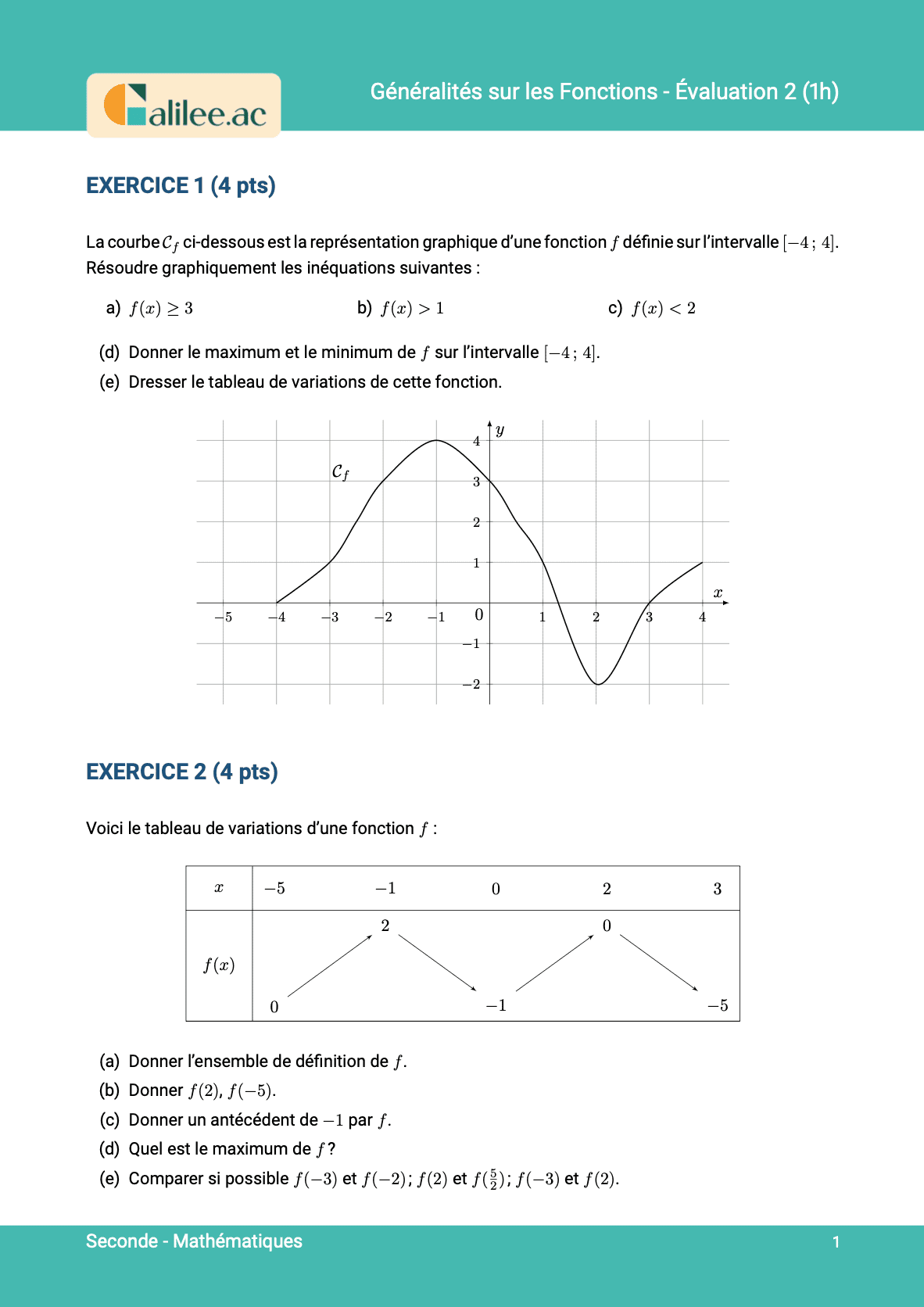
Livre
16. Trouver le maximum et le minimum d'une fonction
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Exercice
5
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour trouver le maximum et le minimum d'une fonction quand on vous a donné sa représentation graphique. On s'y met.Trouver le maximum d'une fonction
Pour trouver le maximum ou le minimum d'une fonction, la première chose à se demander c'est en effet si je regarde cette courbe, vous êtes d'accord avec moi que si j'oublie la partie qui est à droite et que je cherche mon maximum, ça va être ce point là. En revanche, si je regarde toute la courbe, j'ai un doute pour est-ce que le maximum est ici ou est-ce qu'il est ici. Dans l'intervalle sur lequel on va chercher le maximum et où le minimum a son importance. Donc la première question vous demande le maximum de \(f\) sur \([-15, 15]\), c'est à dire d'ici à ici. Attention, pas jusqu'ici. Donc quand je cherche son maximum, je cherche les points les plus hauts. En effet, je vous rappelle que les valeurs d'une fonction, ça se lit pas sur l'axe horizontal, ça se lit sur l'axe vertical. Donc pour savoir si ce point là ou ce point là est plus haut, eh bien je vais reporter à chaque fois la valeur ici et ici et je vais me demander où est-ce que je vais tomber le plus haut possible sur l'axe des ordonnées. Donc le maximum sur \([-15, 15]\) il se joue clairement entre ces deux points. Si vous avez des traits, vous vous rendrez compte que ce point là, il arrive là et que le point là, il arrive légèrement au-dessus. Du coup, le maximum de \(f\) sur \([-15, 15]\) il est atteint pour \(x = -15\). Donc on dit pour \(x = -15\), \(f(x)\) c'est à dire la valeur de \(f\) vaut environ \(12\) et on a notre maximum.Trouver le minimum d'une fonction
Inversement, ici on cherche le minimum sur \([-10, 3]\). Donc il faut bien savoir qu'on va le chercher sur \([-10, -3]\), donc entre ici et ici, on cherche le minimum sur cette portion là. Donc le minimum, c'est encore une fois rapporté à l'axe vertical. Donc le minimum, il est atteint ici pour quelle valeur de \(x\), d'après vous ? Au moins \(8\) et il vaut combien ? \(-2\) ou \(-3\). Donc pour \(x = -8\), \(f(x) = -3\). Je suis content de savoir que mon minimum est bien compris entre \(-10\) et \(-3\), ça veut dire que le point que je donne comme réponse, il est bien compris dans l'intervalle que je cherche et ensuite je donne la valeur de ce minimum. Entraînez-vous, c'est vraiment pas compliqué, limite ça détend un peu le cerveau. On vous a mis des exercices en dessous, à vous de jouer.Nouvelle recrue
Visiteur anonyme
1 pts