Livre
13. Interpréter graphiquement les solutions d'une équation
Conditions d'achèvement
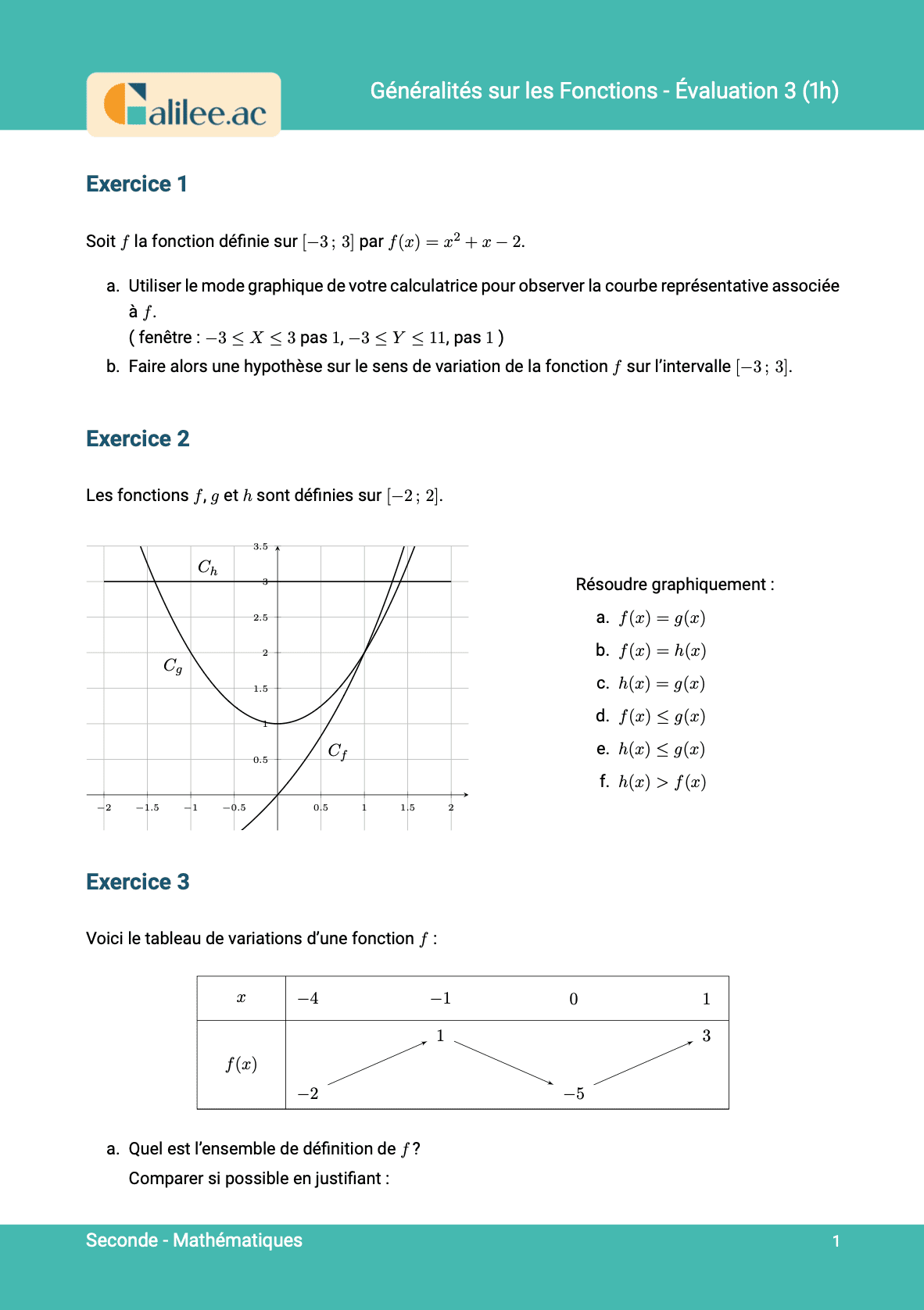
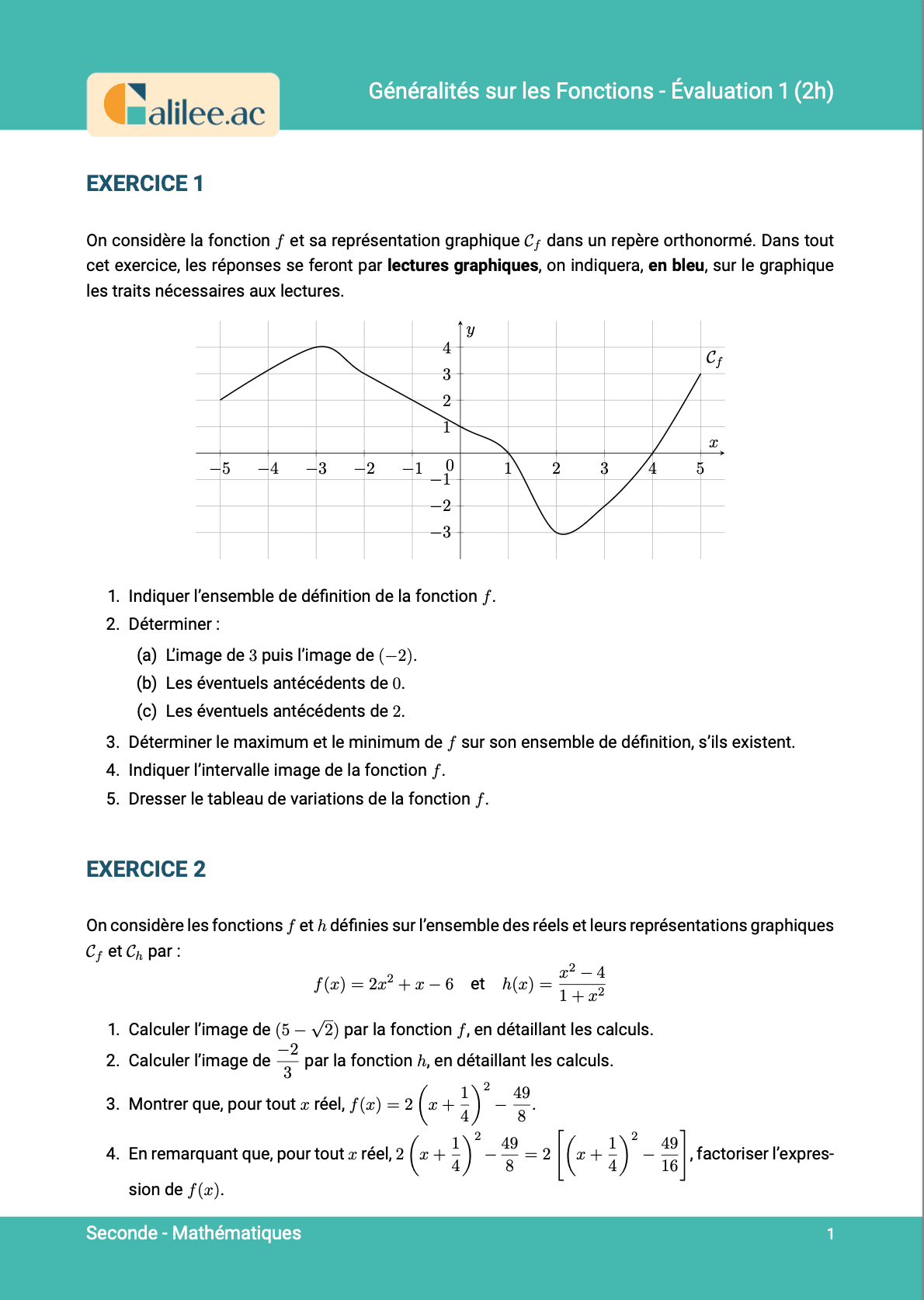
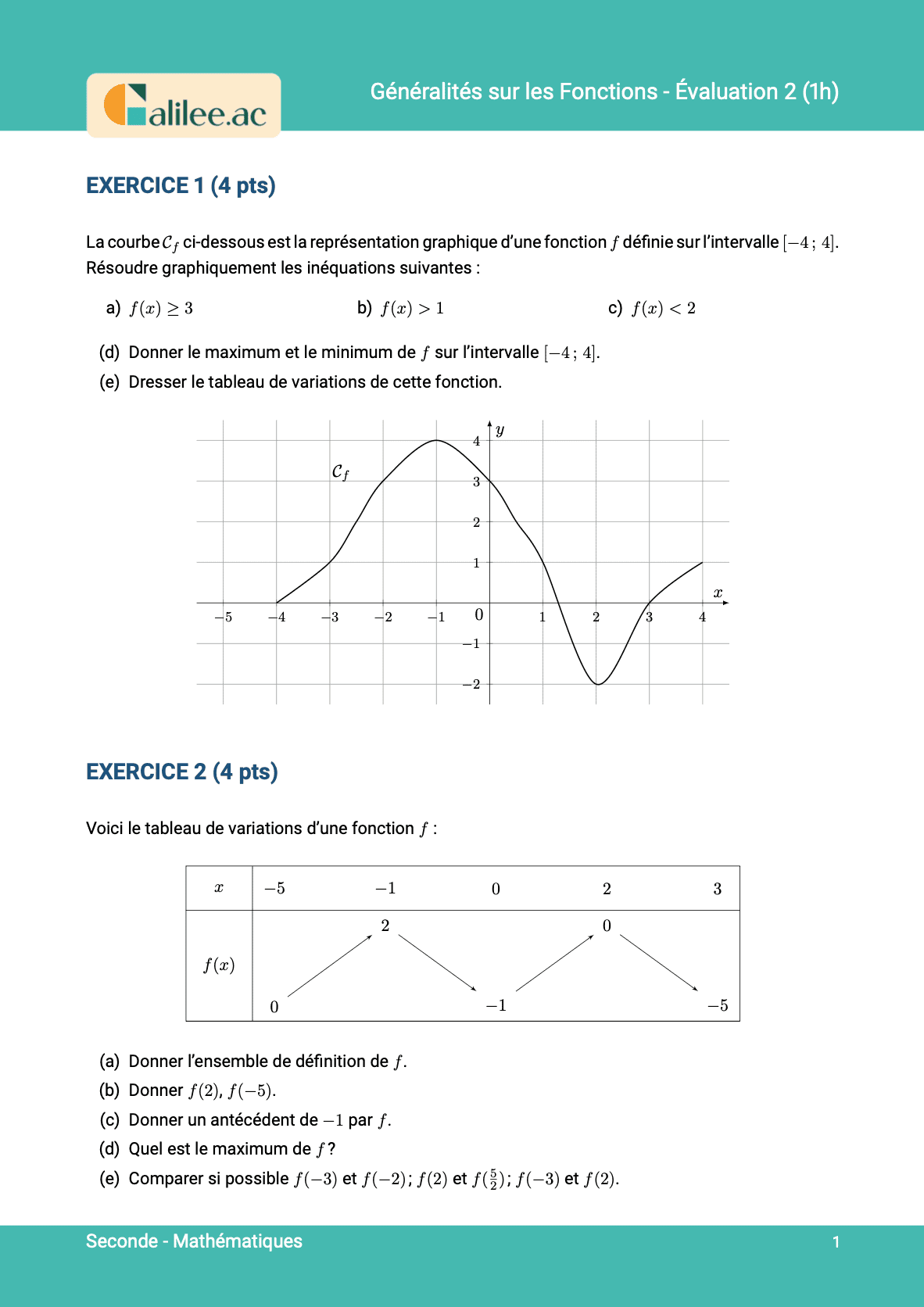
Exercice
1
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Bonjour à tous, dans cette leçon, nous allons voir comment interpréter graphiquement les solutions d'une équation lorsque deux fonctions \(f\) et \(g\) sont données dans l'énoncé.Exemple d'exercice
Un exercice de ce type se présente généralement de la manière suivante : on vous donne une fonction \(f\) et une fonction \(g\), ainsi que les noms des courbes correspondantes, \(C_f\) et \(C_g\). On vous demande dans un premier temps de résoudre une petite équation et dans un deuxième temps d'interpréter graphiquement la solution. La résolution d'équations ne devrait pas vous poser de problème. Par exemple, si je veux résoudre \(5x - 2 = 6\), je vais commencer par passer tous mes \(x\) de l'autre côté. Donc, le \(+6\) va passer de l'autre côté pour devenir \(-6\), donc j'aurai \(5x - x = -6 + 2\). En simplifiant, j'obtiens \(4x = -4\), donc \(x = -1\).Interprétation graphique
Maintenant, comment interpréter graphiquement cela ? Il s'agit de regarder les fonctions \(f\) et \(g\). Supposons que \(g(x) = 5x - 2\) et \(f(x) = x + 1\). En fait, ce qu'on vous a demandé de résoudre, c'était \(g(x) = f(x)\). Vous savez donc que la solution pour que \(g(x)\) soit égale à \(f(x)\) est \(x = -1\). Regardons maintenant ce qui se passe graphiquement. Si je place par exemple \(x = -1\) sur l'axe des abscisses, est-ce que \(g(-1)\) vaut \(f(-1)\) ? Si je lis \(g(-1)\) et \(f(-1)\) sur les ordonnées, est-ce que ces deux valeurs sont égales ? Évidemment, non. Si je me positionne à \(x = -1\), est-ce que \(g(-1) = f(-1)\) ? Toujours pas. Mais si je me positionne à \(x = -1\), vous voyez que \(g(-1) = f(-1)\), autrement dit, quand je suis à \(x = -1\), que je passe par \(f\) ou que je passe par \(g\), j'arrive exactement au même point. Donc, en fait, quand vous résolvez \(g(x) = f(x)\), vous trouvez en fait le point d'intersection de ces deux courbes. Et même mieux que le point, vous trouvez l'abscisse du point d'intersection. Donc, une interprétation graphique, c'est de dire que l'abscisse du point d'intersection de \(f\) et \(g\) est \(-1\). Donc, ce point d'intersection, on va l'appeler \(A\) et on sait que sa première coordonnée est \(-1\). Qu'en est-il de sa deuxième coordonnée ? Comment fait-on pour trouver son ordonnée ? C'est très facile, il suffit de substituer \(-1\) dans \(f\) ou \(g\), vous allez trouver l'ordonnée du point. En fait, que vous substituiez \(-1\) dans \(f\) ou \(g\), vous allez arriver au même résultat. En l'occurrence, \(f(-1)\) va donner \(-1 + 1 = 0\), donc le point d'intersection de ces deux courbes est \((-1, 0)\). Cela fonctionne aussi dans l'autre sens. On peut vous demander directement de déterminer le point d'intersection de \(f\) et \(g\), auquel cas vous résolvez \(g(x) = f(x)\), vous utilisez l'interprétation graphique et vous substituez la solution dans \(f\) ou \(g\) pour trouver l'ordonnée.Conclusion
Voilà, j'espère que cette leçon vous a aidé à comprendre comment interpréter graphiquement les solutions d'une équation. N'hésitez pas à vous entraîner avec des exercices pour bien maîtriser ce concept. Bonne continuation !Recrue
Visiteur anonyme
11 pts