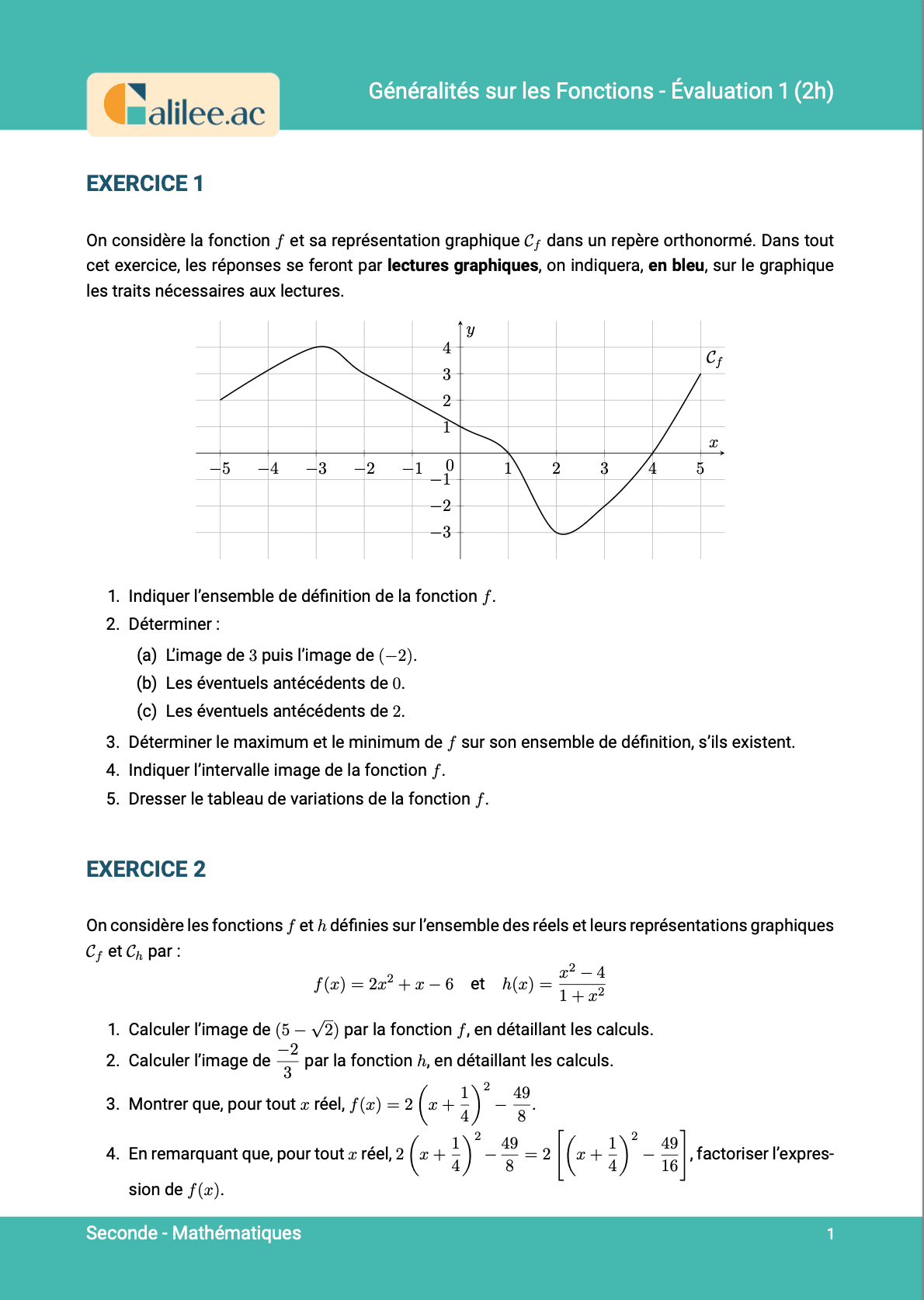
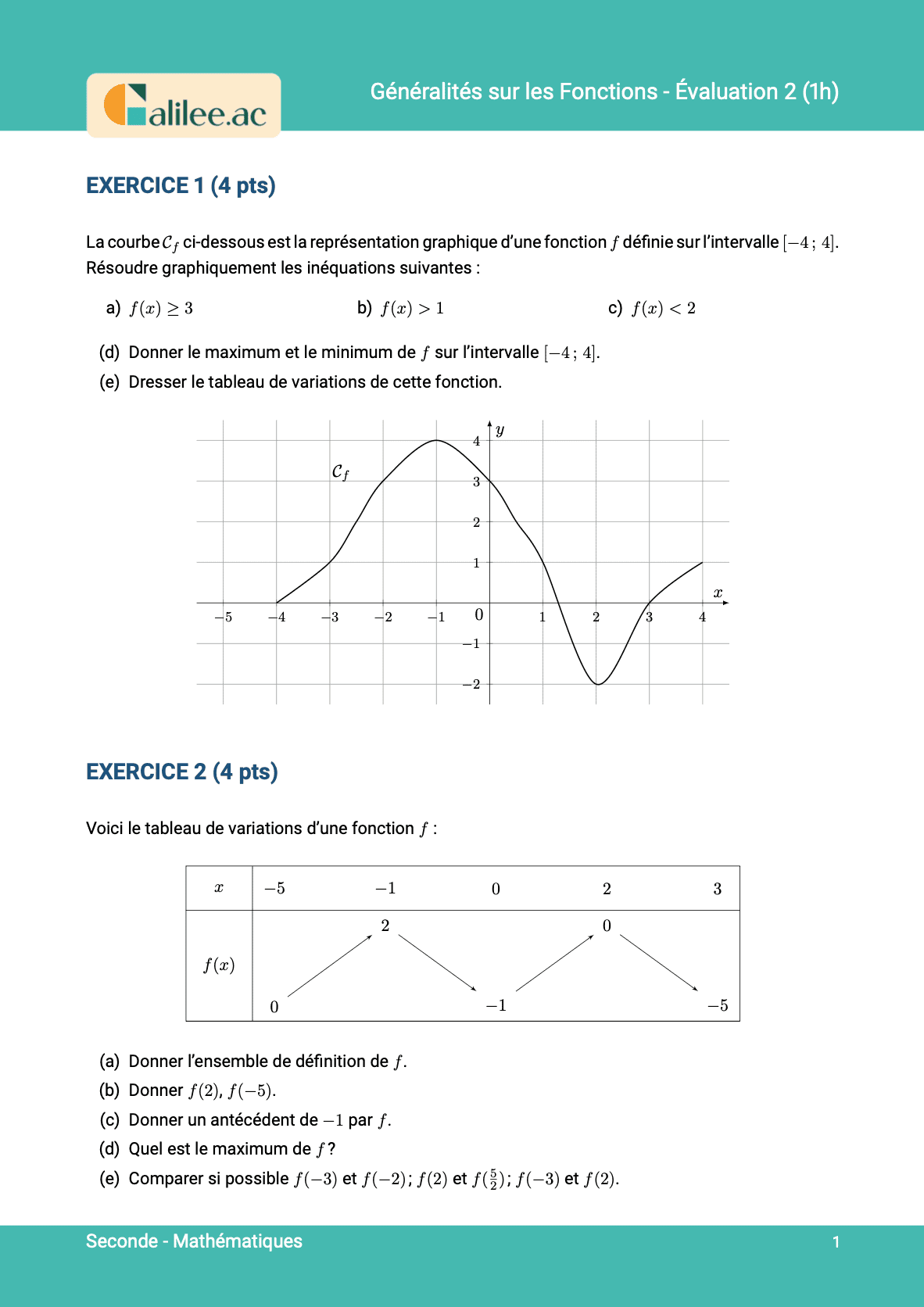
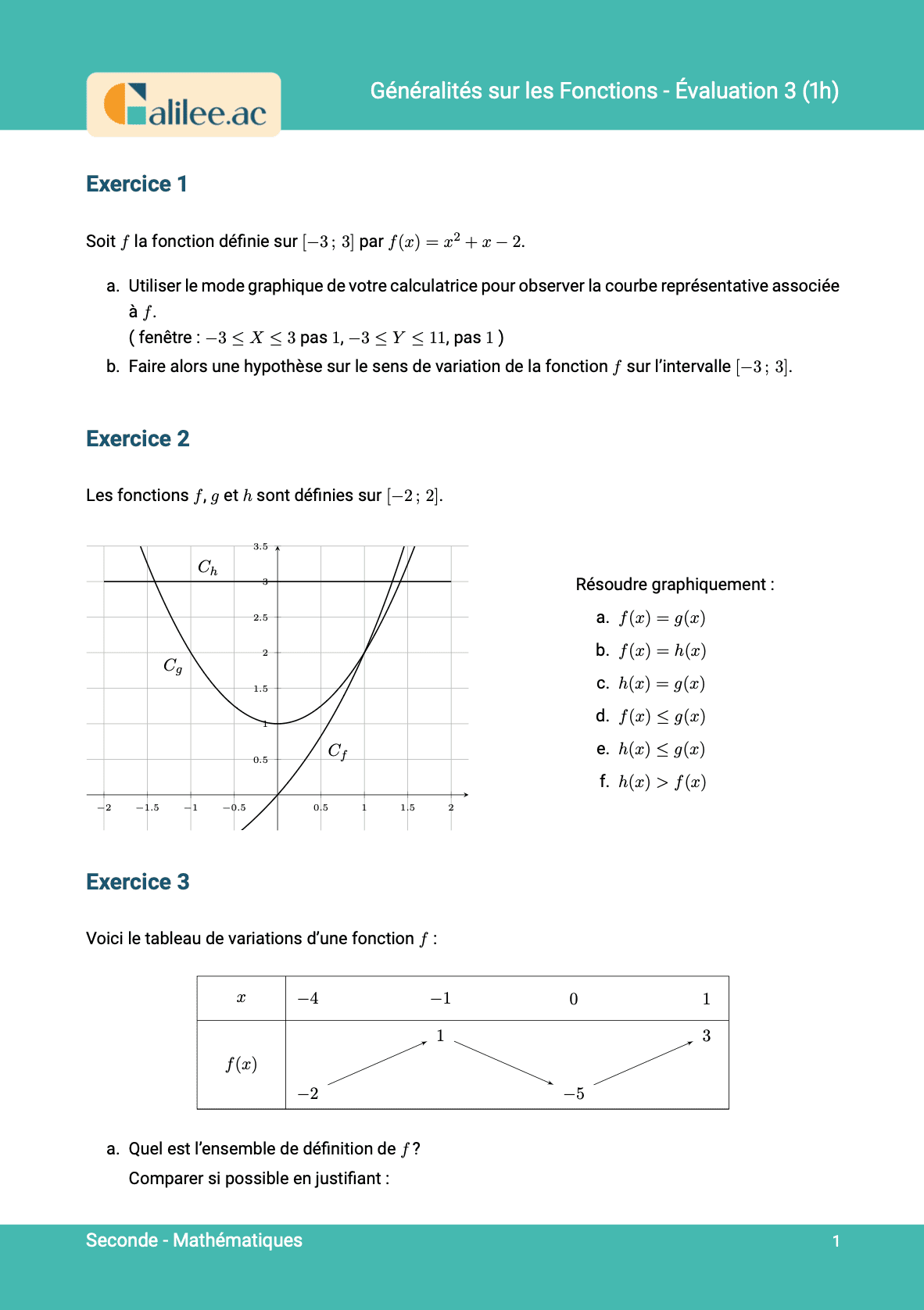
11. Savoir si un point appartient à une courbe représentative

Introduction

Ah, les amis, nous allons voir en 30 secondes comment savoir si un point appartient à la courbe représentative d'une fonction. Allons-y.

Comprendre la courbe représentative d'une fonction

Ce que j'aimerais que vous reteniez tout au long de votre parcours au lycée, c'est que si un point \(A\) appartient à \(C_f\), la courbe représentative de \(f\), c'est-à-dire la courbe qui donne une allure de \(f\), alors par exemple, notre fonction \(f\) pourrait avoir à peu près cette tête-là. Si ce point \(A\) est à (1,2) par exemple, si mon point \(A\) est ici, vous êtes d'accord avec moi que le 1 va apparaître ici et le 2, on va le faire apparaître ici, pourquoi pas. On lit toujours les abscisses et les ordonnées, horizontal et vertical. On mettra notre 1 ici, notre 2 ici.

Comment vérifier si un point appartient à la courbe

De manière générale, quand \(x\) est ici, ce que je vais lire ici, quand je passe par la fonction \(f\), c'est \(f(x)\). Donc, quand je pars de 1 et que je vais sur l'axe vertical, ce que je devrais lire ici à priori, ça sera \(f(1)\). Donc, pour vérifier que le point est bien dessus, vous prenez la première coordonnée, vous la mettez dans la fonction et vous voyez si vous obtenez la deuxième. Autrement dit, est-ce que \(f(1)\) vaut 2 ? Sauf que \(f(1)\), je peux le calculer rapidement. J'ai l'expression de la fonction : \(f(1) = 3 \times 1^2 - 2 \times 1 + 1\). Ça me fait \(3 - 2 + 1\), ça me fait 2. Je retrouve bien mon 2. Du coup, on a bien notre point \(A\) qui est tel que \(f(1) = 2\) et du coup, notre point \(A\) est sur la courbe. Retenez que de manière générale, quand votre point est sur la courbe, ce qu'on a, c'est \(x, f(x)\). Autrement dit, chaque couple de nombres qui est sur la courbe, je peux mettre ce que je veux tant que ce que je mets en deuxième coordonnée est l'image du premier point. Il y a des exercices en dessous, entraînez-vous, car il y a des élèves en terminale qui ne savent toujours pas répondre à ce genre de questions, alors que c'est vraiment une compétence ultra utile. Allez, les amis, des exercices en dessous, à vous de jouer.