Livre
10. Résoudre graphiquement f(x) ≤ g(x)
Conditions d'achèvement
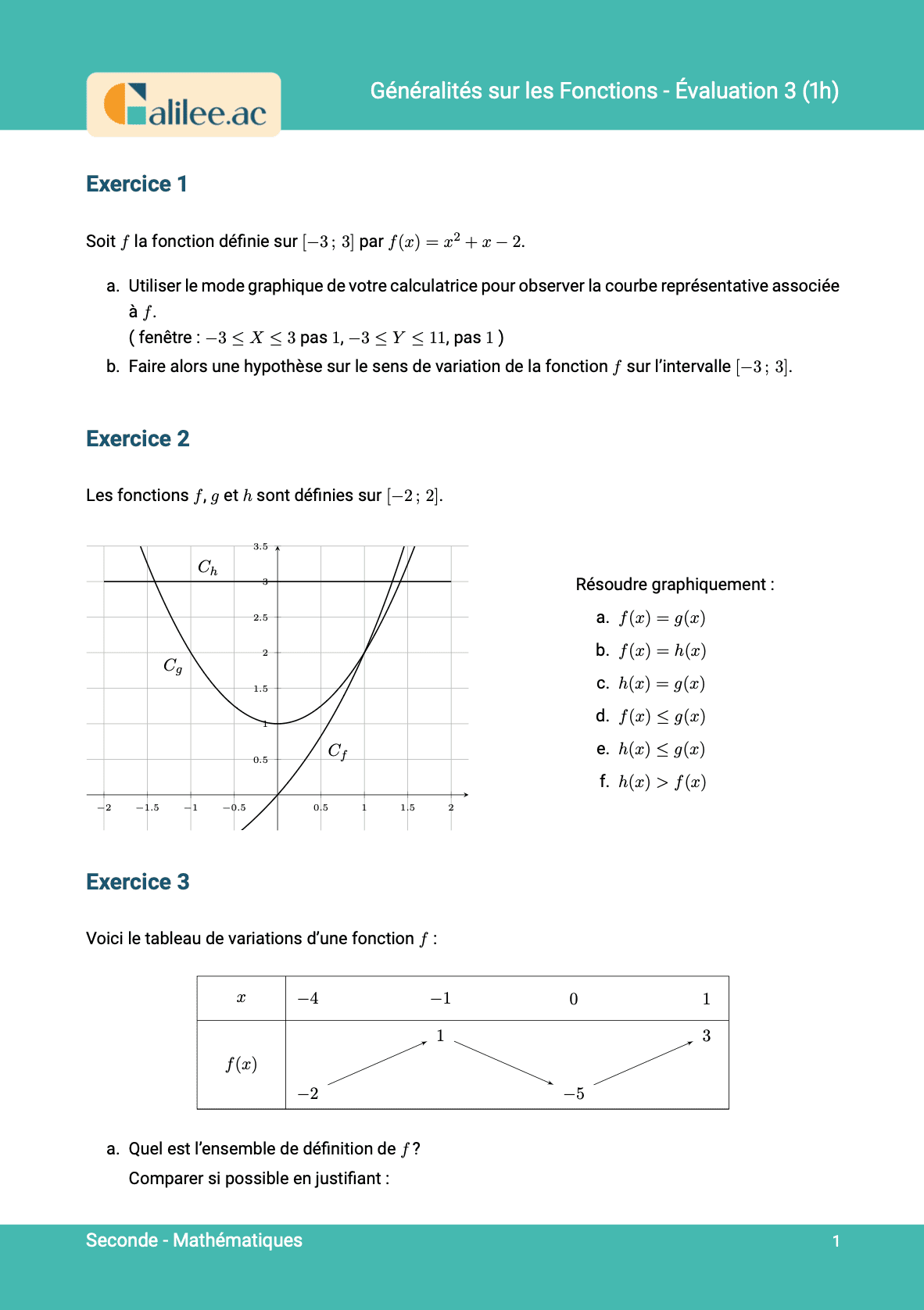
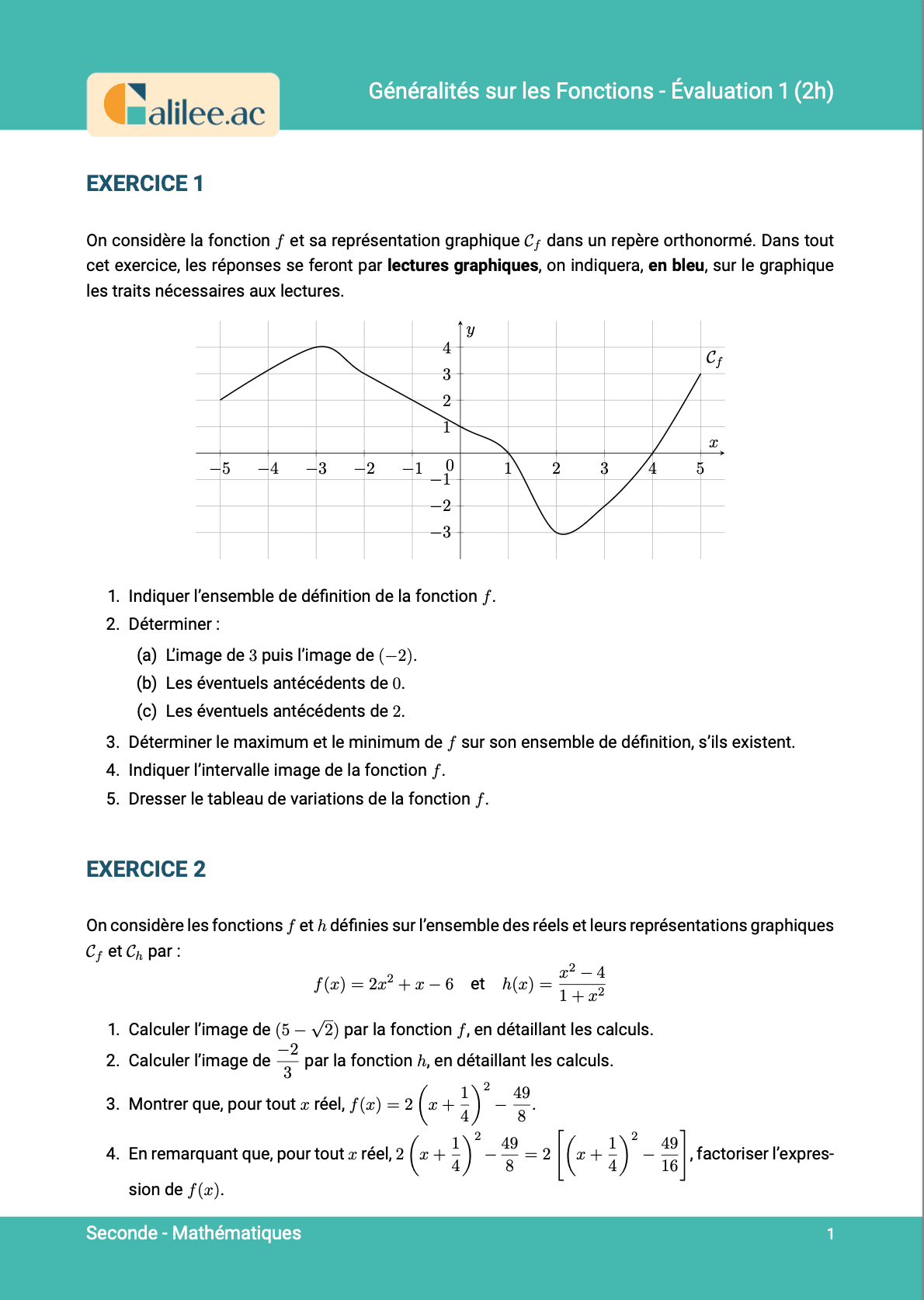
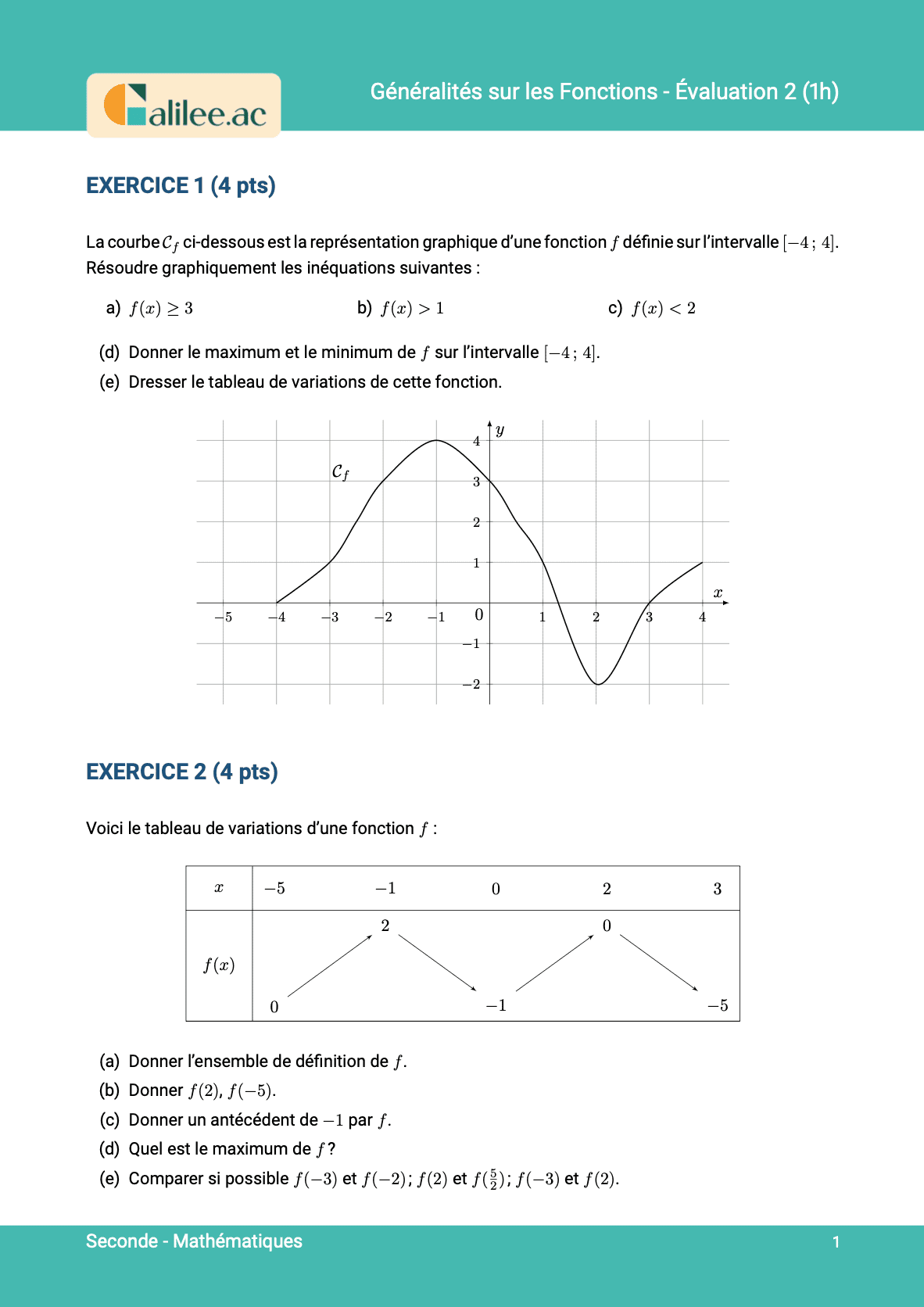
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Exercice
5
Pour aller plus loin : Contrôles sur ce chapitre 🎯
SecondeRecommandé
Contrôle Vecteurs, fonctions et équations - sujet 21
Chapitres: Vecteurs Fonctions de référence ...
SecondeRecommandé
Contrôle Généralités sur les Fonctions 2
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Nombres, repérage, fonctions et calcul - sujet 15
Chapitres: Ensembles de nombres Vecteurs ...
SecondeRecommandé
Contrôle Généralités sur les Fonctions 1
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Fonctions et équations - sujet 8
Chapitres: Étude de fonctions Résolution d'équations
SecondeRecommandé
Contrôle Étude de fonctions et fonctions de référence - sujet 22
Chapitres: Étude de fonctions Fonctions de référence
SecondeRecommandé
Contrôle Inéquations et fonctions - sujet 9
Chapitres: Résolution d'inéquations Fonctions affines ...
SecondeRecommandé
Contrôle Vecteurs, inéquations et fonctions - sujet 16
Chapitres: Vecteurs Résolution d'inéquations ...
SecondeRecommandé
Contrôle Fonctions de référence et fonctions affines - sujet 13
Chapitres: Étude de fonctions Fonctions affines ...
SecondeRecommandé
Contrôle Pourcentage évolution, Inéquation, Fonctions généralité, affines et Carrées
Chapitres: Résolution d'inéquations Étude de fonctions ...
SecondeRecommandé
Contrôle Généralités sur les Fonctions 3
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Fonctions et calcul numérique - sujet 10
Chapitres: Étude de fonctions Calculs numériques et littérals
merci !
Introduction
Allez mes amis, on est parti pour voir en 3 minutes comment résoudre une inégalité avec deux fonctions \(f\) et \(g\). Sachant qu'on vous a représenté ces fonctions, il n'y a rien de plus simple que de résoudre \(f(x)\) plus petits ou plus grands que \(g(x)\).Explication de la méthode
Vous regardez votre voie de fonction, vous vous dites : si \(f\) est plus petit que \(g\), ça veut dire que la fonction \(f\) va être en dessous de la fonction \(g\). Vous regardez ces deux fonctions, vous voyez que quand on se déplace dans ce sens là, il y en a toujours une qui est au dessus de l'autre. Si je place n'importe où, par exemple en -12, je me rends compte que la fonction \(f\) est au dessus de la fonction \(g\). Il vous suffit de réfléchir à quand est-ce que votre fonction \(f\) est non pas au dessus mais en dessous de la fonction \(g\). Dans ce cas là, je vois qu'ici la fonction \(f\) est au dessus. Si je me déplace juste à côté, ça ne changerait pas. Par contre, on aurait un changement ici et là on aurait un autre changement.Conclusion
Du coup, finalement, les endroits où ma fonction \(f\) est en dessous, c'est ici sur cette zone qu'on a là, donc entre -10 et -3. Donc les endroits où \(f(x)\) est plus petit que \(g(x)\) est quand \(x\) appartient à -10 jusqu'à -3. Est-ce que je garde -10 et -3 ? Oui, parce que c'est inférieur ou égal, donc je veux garder la possibilité que ces deux fonctions soient égales. Donc ces deux nombres qui correspondent à la transition et au cas d'égalité, je les garde. On vous a mis des petits exercices avec des fonctions comme ça, vous avez quasiment fini l'étude graphique. Ne lâchez pas, vous êtes des machines, vous allez y arriver.Nouvelle recrue
Invité
0 pts
