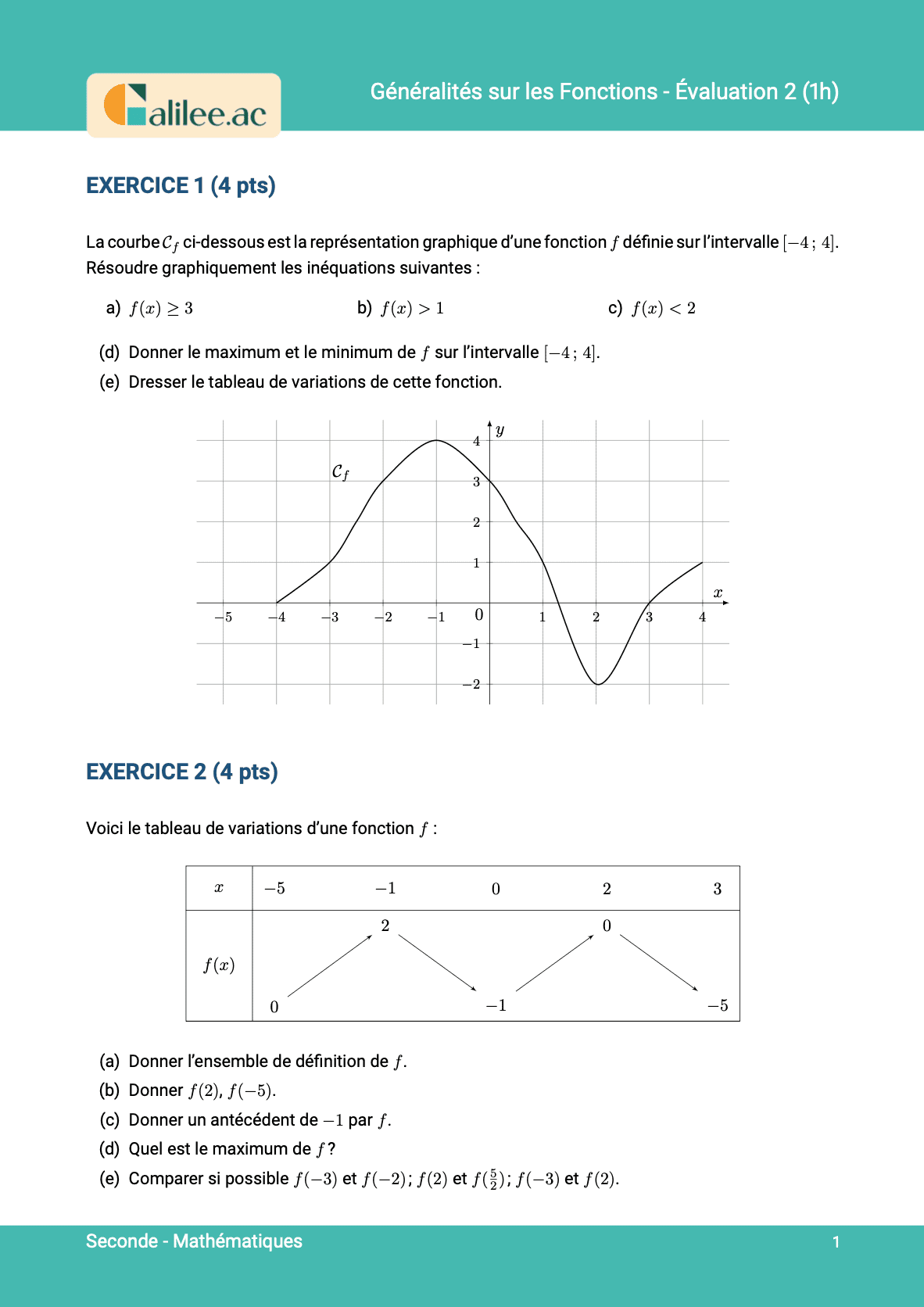
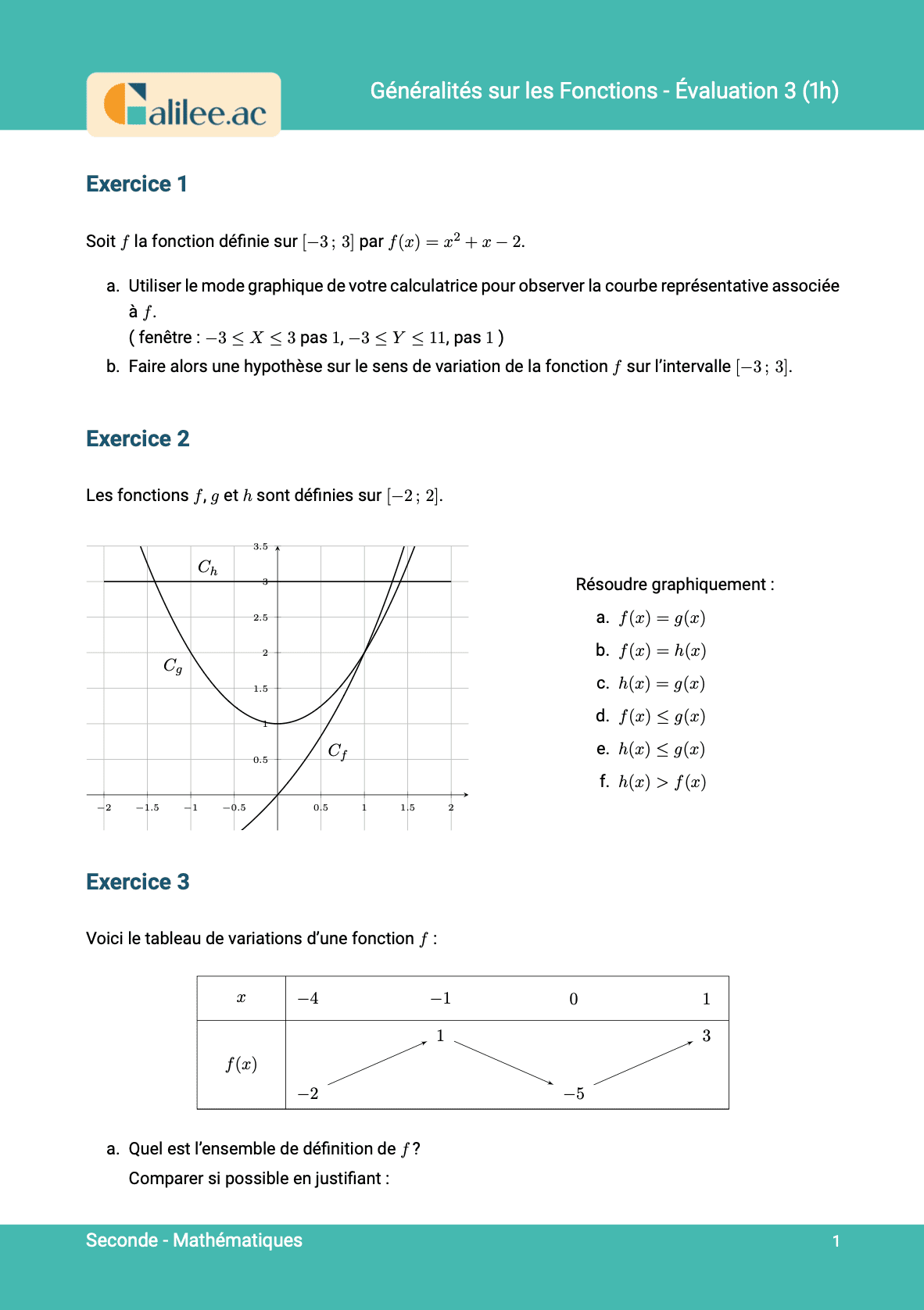
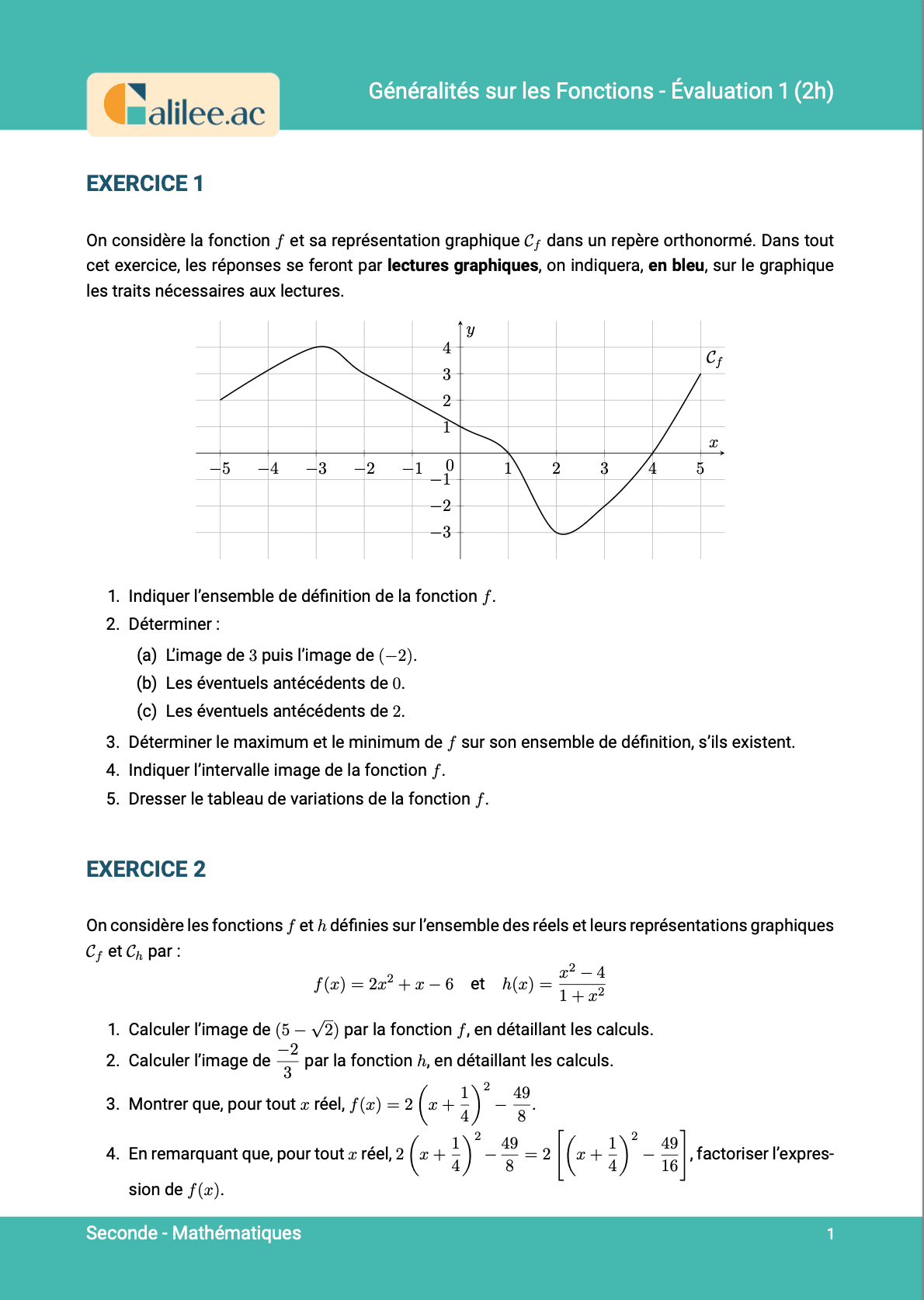
9. Résoudre graphiquement f(x) ≤ k

Introduction

Allez les amis, on est parti pour utiliser la règle et les stylos pour voir comment résoudre graphiquement une inégalité. Sachant qu'on vous a donné la représentation graphique de la fonction, nous allons résoudre \(f(x) < 5\).

Étapes de résolution

La première étape va être de faire apparaître le 5 sur l'axe vertical. Ensuite, comme d'habitude, on trace une droite horizontale qui passe par ce point 5. La troisième étape va être de faire apparaître les zones qui nous intéressent. Nous voulons que \(f(x)\) soit plus petit que 5, autrement dit que l'image de \(x\) soit plus petite que 5. On sait que notre droite va couper la fonction à plusieurs points, donc on sait que ces points sont importants. Ensuite, on va tester si l'image est bien dans la zone que nous recherchons. Si ce n'est pas le cas, on élimine cette zone. On répète ce processus pour toutes les zones.

Conclusion

Au final, les zones qui nous intéressent sont celles où l'image est dans la zone rouge. Vous savez maintenant représenter deux intervalles qu'on veut réunir. On va utiliser une union pour dire que \(x\) appartient à cet intervalle qui va de -10 jusqu'à -5 et on va unir cet intervalle avec l'intervalle qui va de 3 jusqu'à 7. La question qu'on peut se poser maintenant est de savoir si on va garder -10 et -5, et si on va garder 3 et 7. Nous voulons que \(f(x)\) soit inférieure ou égale à 5. Pour chacun des points, on arrive exactement à 5. Autrement dit, pour nos quatre points, l'image vaut 5. Or, on a \(f(x) \leq 5\), sous-entendu \(f(x)\) peut valoir 5. Donc, tous ces points, je vais les garder en fermant les crochets. Donc, notre solution est cette union d'intervalles. Je trace ma droite, ensuite je colorie la zone qui m'intéresse (\(f(x) < 5\)), ensuite je fais apparaître les points d'intersection et je me demande pour chaque intervalle si ça m'amène dans ma zone ou en dehors de ma zone. Il vous reste des petits exercices à faire, c'est très simple, vous pouvez le faire. À vous de jouer!