Représenter graphiquement une fonction à partir d'un tableau: exercices corrigés 🚀

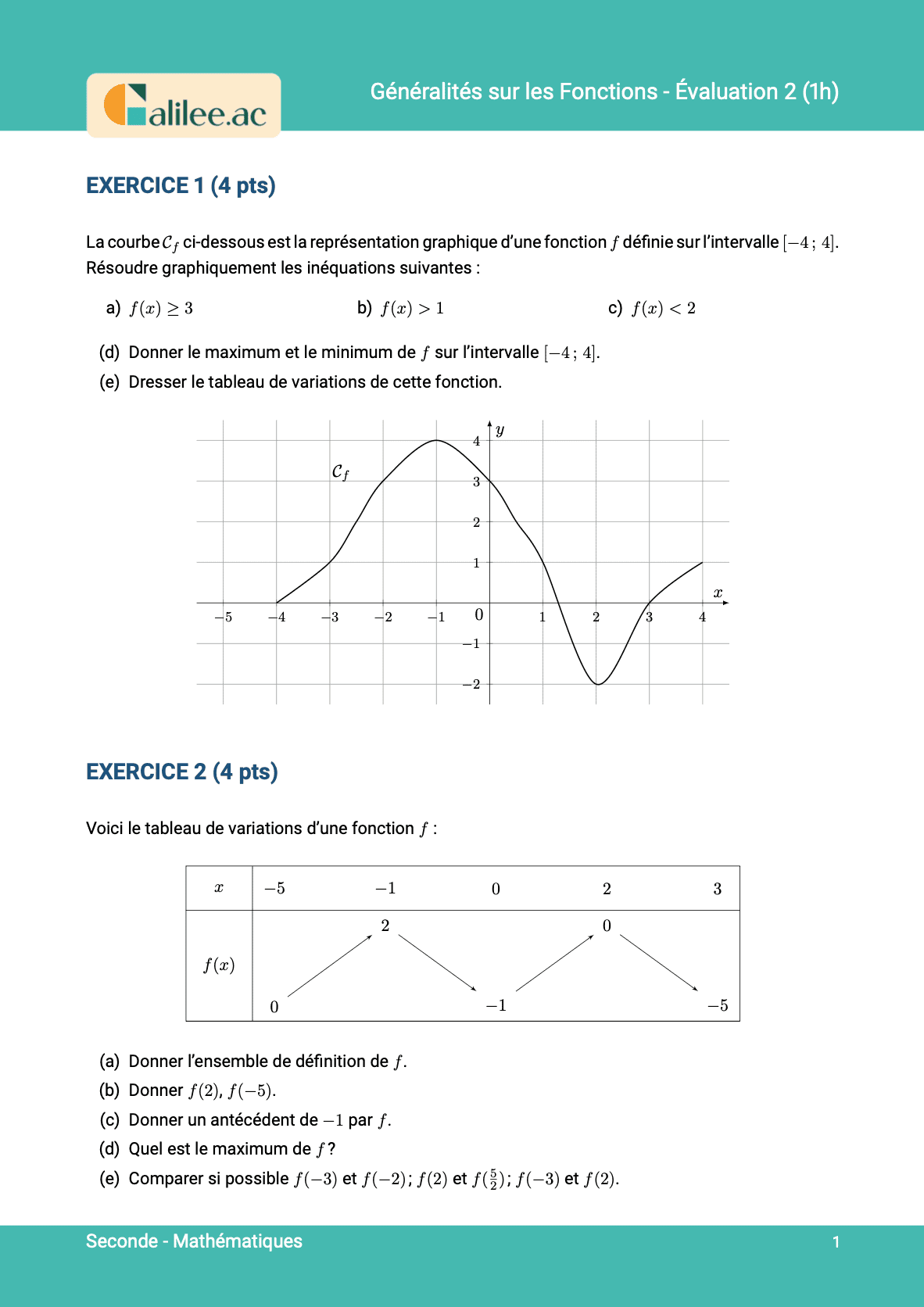
Exercice 1

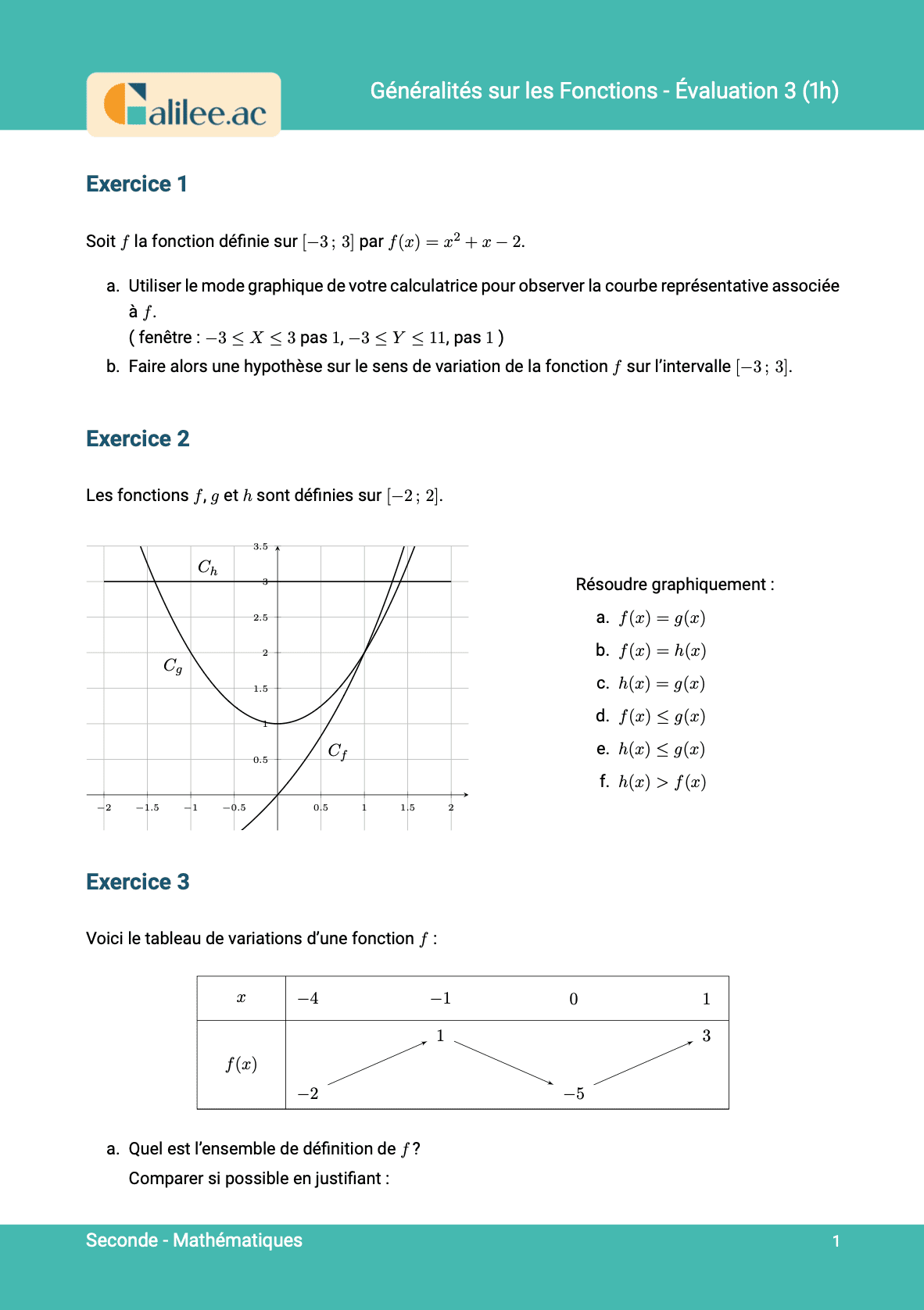
Exercice 2

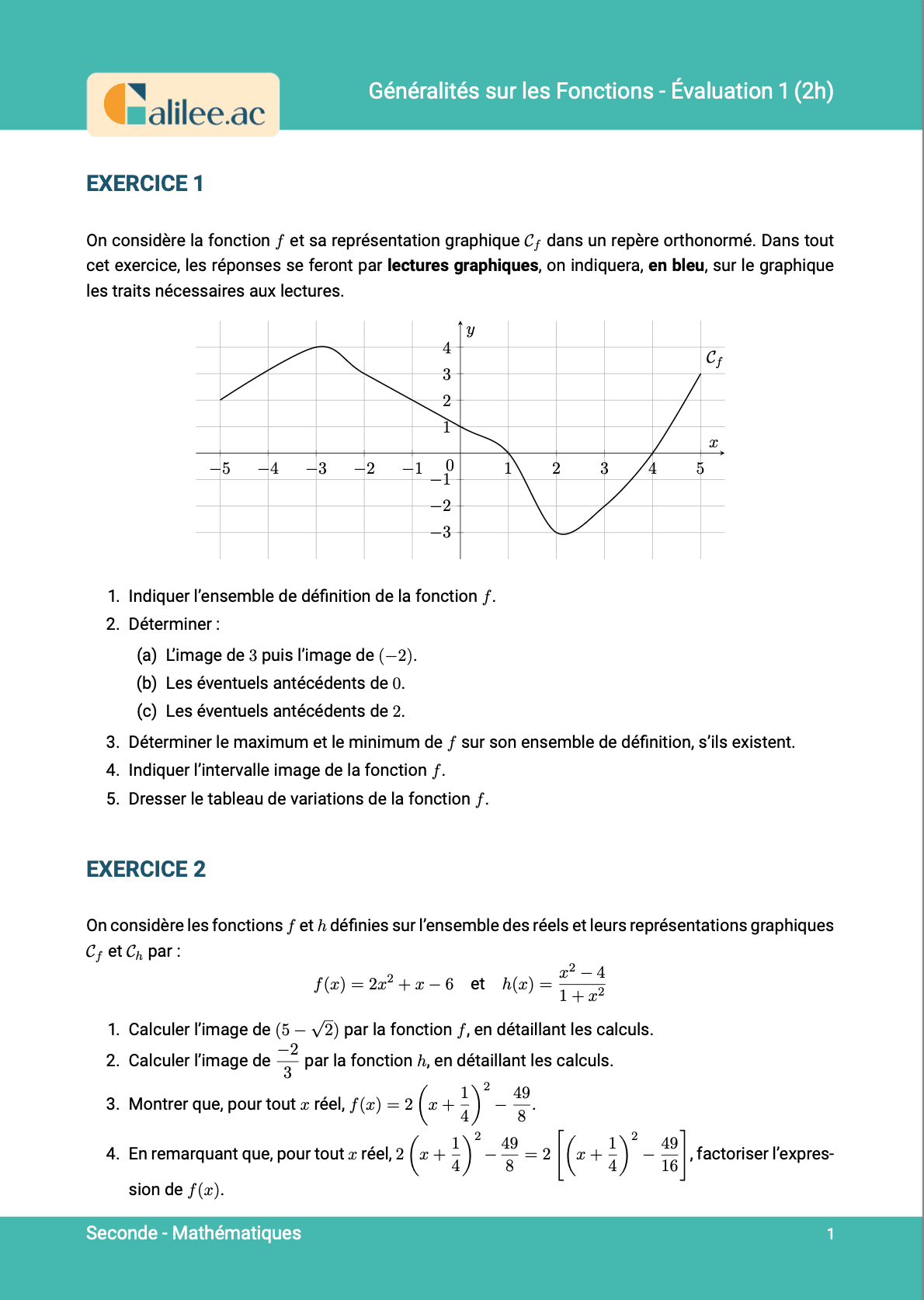
Exercice 3

Pour aller plus loin : Contrôles sur ce chapitre 🎯

SecondeRecommandé

Contrôle Nombres, repérage, fonctions et calcul - sujet 15

Chapitres: Ensembles de nombres Vecteurs ...

Voir le sujet

SecondeRecommandé

Contrôle Fonctions et équations - sujet 8

Chapitres: Étude de fonctions Résolution d'équations

Voir le sujet

SecondeRecommandé

Contrôle Généralités sur les fonctions - sujet 4

Chapitres: Étude de fonctions

Voir le sujet

SecondeRecommandé

Contrôle Inéquations et fonctions - sujet 9

Chapitres: Résolution d'inéquations Fonctions affines ...

Voir le sujet

SecondeRecommandé

Contrôle Généralités sur les fonctions - sujet 5

Chapitres: Étude de fonctions

Voir le sujet

SecondeRecommandé

Contrôle Vecteurs, inéquations et fonctions - sujet 16

Chapitres: Vecteurs Résolution d'inéquations ...

Voir le sujet

SecondeRecommandé

Contrôle Généralités sur les Fonctions 1

Chapitres: Étude de fonctions

Voir le sujet

SecondeRecommandé

Devoir commun Calcul, vecteurs et fonctions - sujet 36

Chapitres: Calculs numériques et littérals Vecteurs ...

Voir le sujet

SecondeRecommandé

Devoir commun Fonctions, vecteurs et inéquations - sujet 26

Chapitres: Étude de fonctions Fonctions affines ...

Voir le sujet

SecondeRecommandé

Devoir commun Fonctions, vecteurs et taux d'évolution - sujet 25

Chapitres: Étude de fonctions Vecteurs ...

Voir le sujet

SecondeRecommandé

Contrôle Vecteurs, fonctions et équations - sujet 21

Chapitres: Vecteurs Fonctions de référence ...

Voir le sujet

SecondeRecommandé

Contrôle Généralités sur les Fonctions 3

Chapitres: Étude de fonctions

Voir le sujet

Introduction

Allez les amis, on est parti pour apprendre à représenter une fonction à partir d'un tableau de valeurs. Ce qu'il faut que vous compreniez quand on vous donne un tableau de valeurs et qu'on vous demande de représenter la fonction, c'est qu'en gros dans votre tableau de valeurs, il y a deux lignes. La première ligne qui correspond à \(x\) et la deuxième qui correspond à \(f(x)\). Chacun de ces couples de coordonnées est un point. Donc j'ai 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 points à représenter sur mon graphique.

Comprendre les coordonnées

Est-ce que -6 correspond à l'abscisse 6 de mon point (-6, 4) ou est-ce que cela correspond à l'ordonnée ? Cela correspond à l'horizontale, parce que c'est quand \(x\) varie que l'on se déplace verticalement. Donc, j'aimerais que vous vous rappeliez que \(f(x)\) c'est l'image de \(x\). Donc cette ligne là, ça correspond forcément aux images et on a vu dans la première vidéo que les images, c'est le nombre qu'on met verticalement sur cet axe là.

Représenter les points sur le graphique

Donc si je prends mon premier point (-6, -4), ça veut dire que sur l'axe vertical, l'ordonnée du point ça va être -4 et sur l'axe horizontal, ça va être -6. Donc je cherche un point qui a cette ordonnée et cette abscisse, le seul point qui a ça, il est ici. Donc mon premier point, je le place ici. Je continue avec (-4, -3), je suis ici. Pour le point (-3, -3), il n'a pas changé d'ordonnée, je le place ici. Pour (-1, 0), je suis ici, ça vaut zéro en effet verticalement. Ici, j'ai bien une ordonnée de zéro et une abscisse de -1. On continue, quand \(x = 0\), je suis à 2, donc là c'est le point d'abscisse 0 et d'ordonnée 2. Quand je suis à 1, ça vaut 3. Quand je suis à 3, ça vaut 4 et ensuite pour 5 et 6, c'est la même chose.

Tracer la fonction

Une fois que j'ai placé mes points, j'ai plus qu'à prendre la main et simplement tracer une fonction qui passe par tous ces points. Je sais pas si j'ai été très souple, mais en tout cas, c'est lié. Évidemment, les plus malins d'entre vous me diront que cette fonction là que je dessine, elle marcherait aussi. En effet, elle passe par tous les points. Donc quand vous représentez une fonction, vous ne représentez jamais exactement la fonction réelle parce que ce tableau là, il ne donne pas d'information sur ce qui se passe entre deux points sur la courbe. Vous représentez toujours une fonction \(f\) qui pourrait matcher avec ce tableau.

Conclusion

On vous a mis des exercices. Vous avez au début de seconde, quand vous commencez à l'analyse, toujours la même difficulté : c'est de savoir reconnaître qu'est-ce que l'image, qu'est-ce que c'est l'ordonnée, l'image, l'antécédent, l'abscisse, l'ordonnée, l'horizontal, le vertical. Une petite astuce, c'est que les images s'associent verticalement, les ordonnées c'est vertical et que les antécédents s'associent horizontalement, les abscisses c'est horizontal. On vous a donné des exercices, faites-vous une belle fiche avec un joli dessin à vous tous.

Nouvelle recrue

Invité

0 pts