Livre
5. Résoudre une équation
Conditions d'achèvement
Consulter
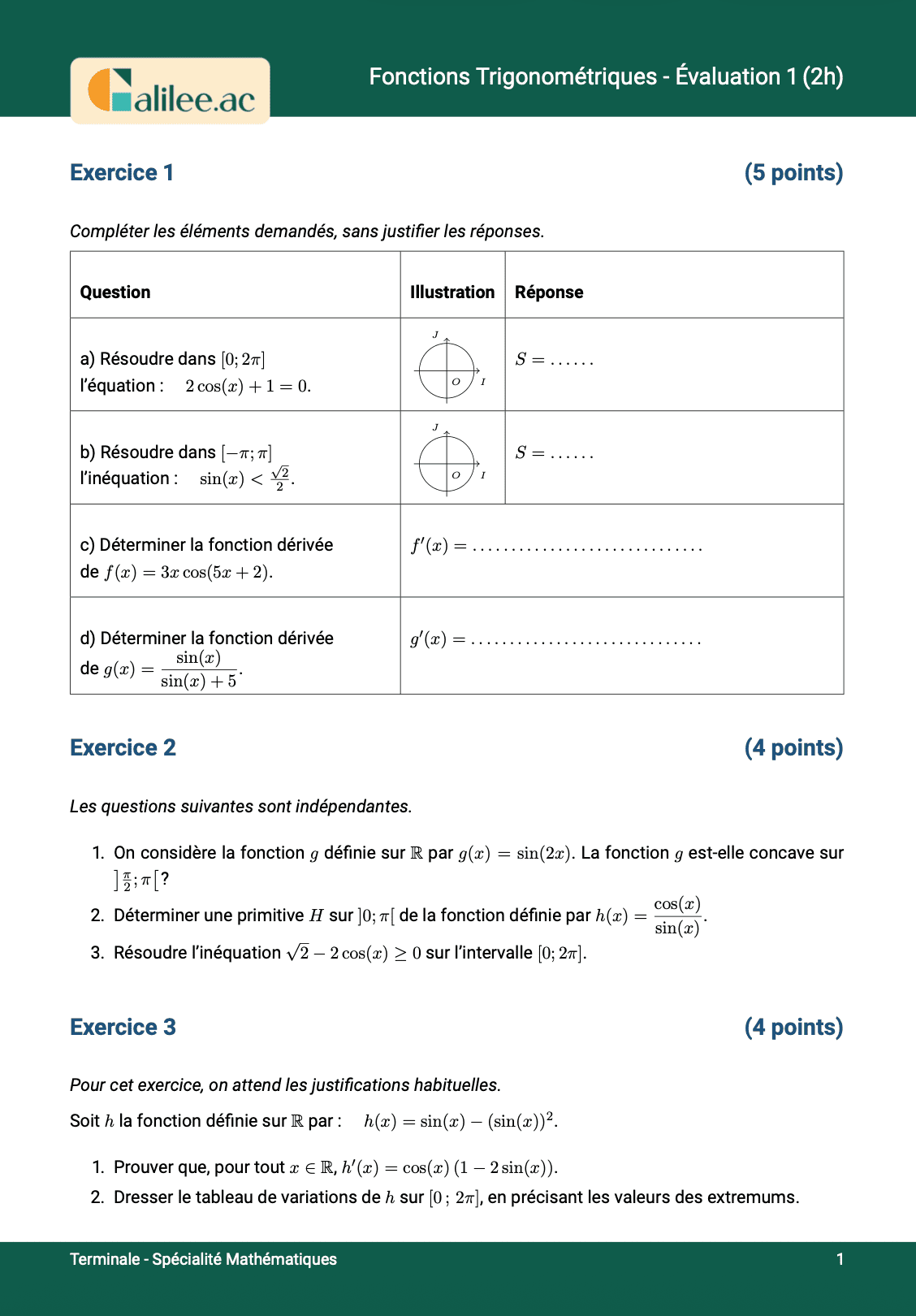
Exercice
1
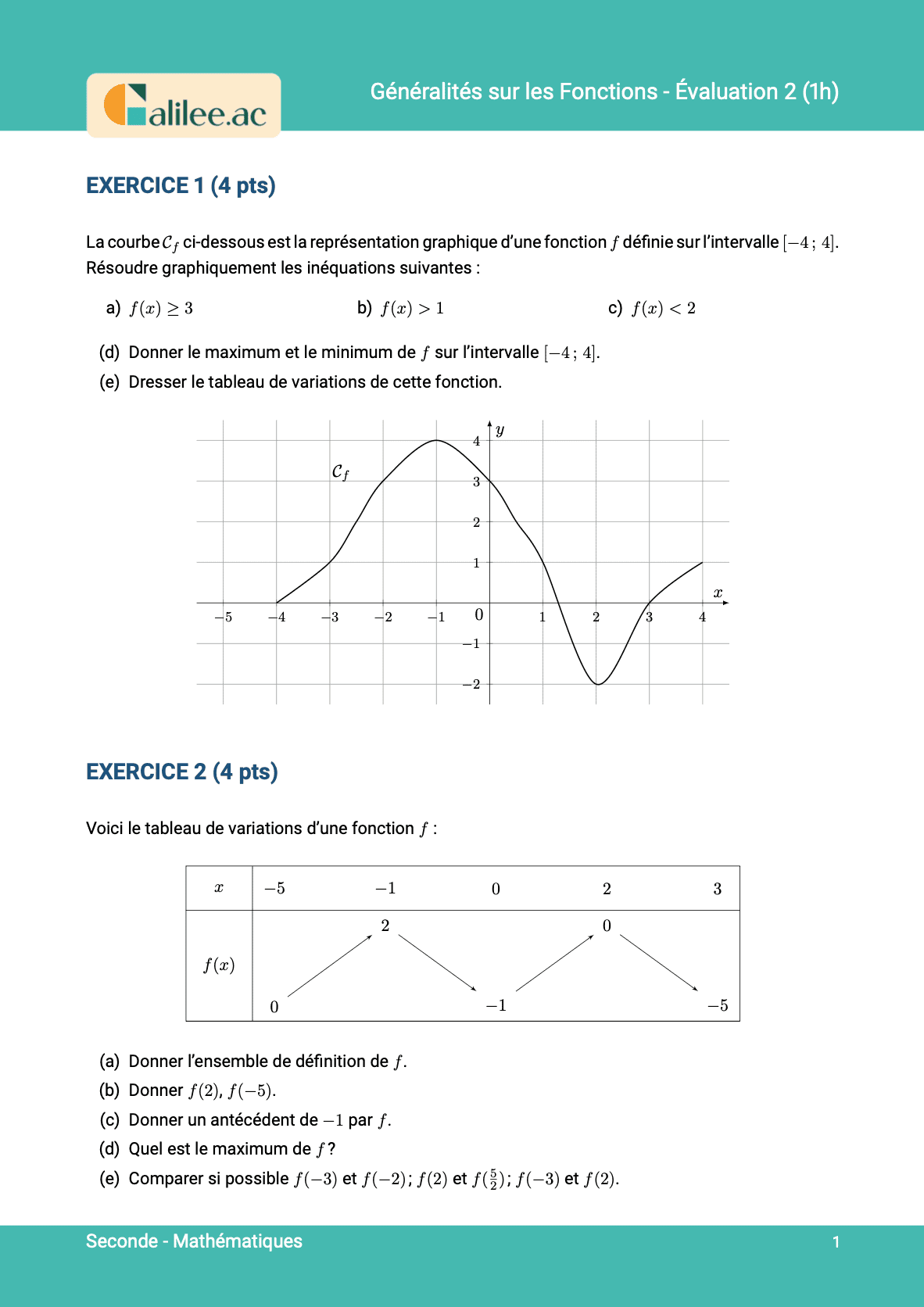
Exercice
2
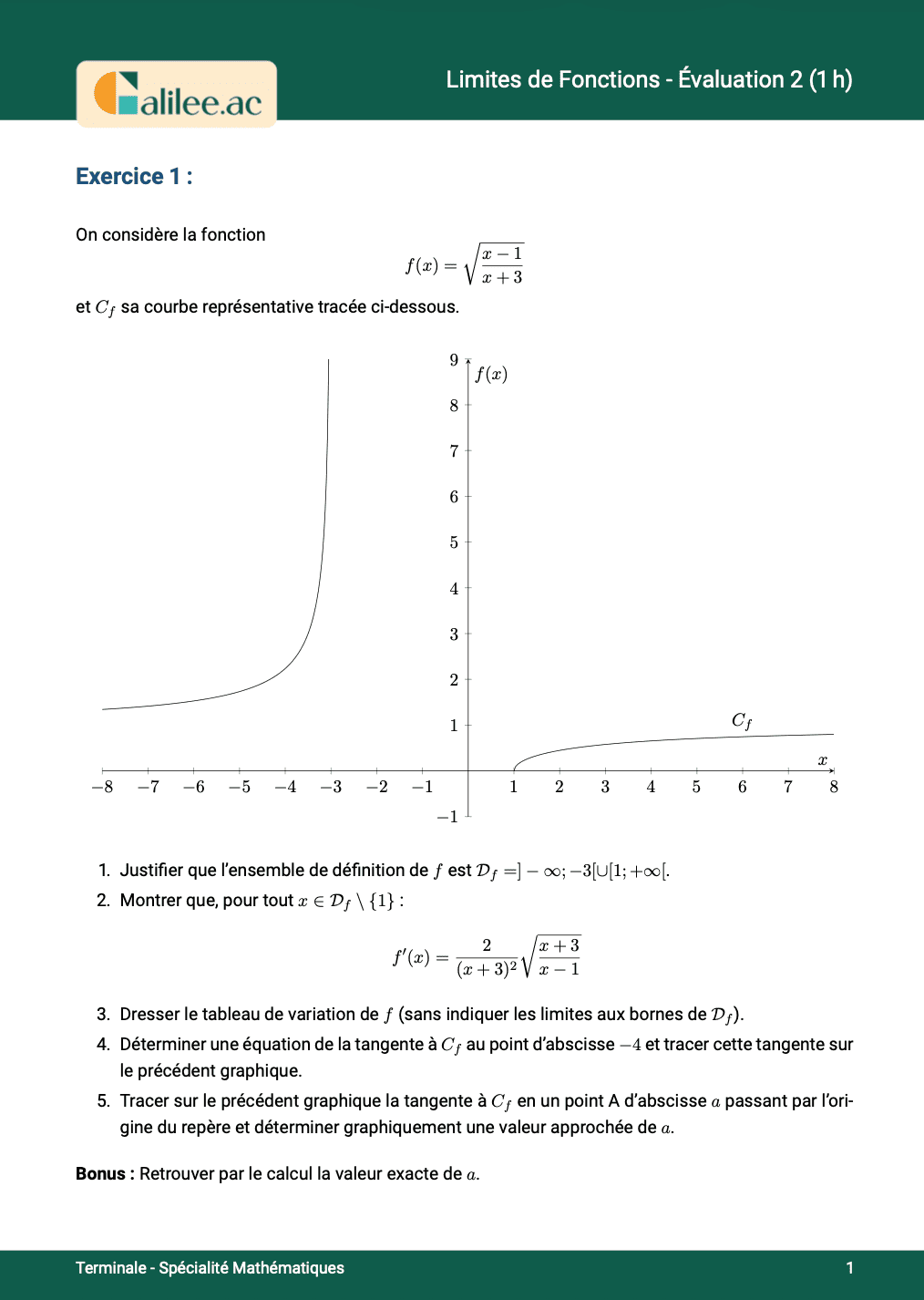
Exercice
3
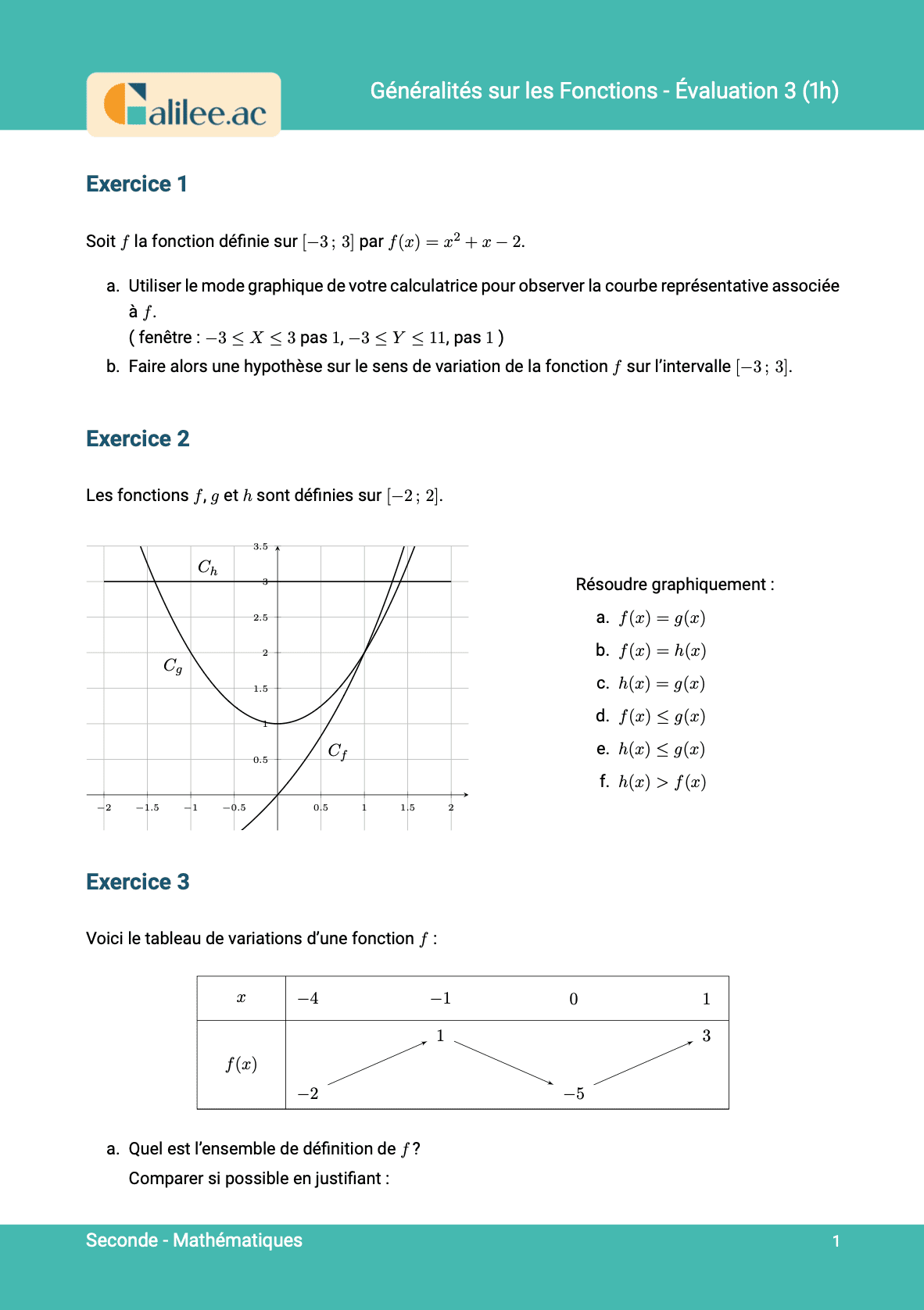
Exercice
4
Exercice
5
Exercice
6
Exercice
7
Exercice
8
Exercice
9
Exercice
10
Exercice
11
Exercice
12
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Dans cette nouvelle vidéo, nous allons aborder les résolutions d'équation. Nous nous intéressons particulièrement au cas où nous avons un facteur qui multiplie un terme de premier degré, c'est-à-dire une équation de la forme \(a(bx + c) = 0\).Exemple particulier
Prenons un exemple un peu particulier. Vous remarquerez que nous ne sommes pas exactement dans le cas décrit précédemment. Cependant, je l'ai choisi car nous allons le traiter de la même manière. Supposons que nous ayons une équation où quelque chose multiplie et à cela s'ajoute un autre terme. Par exemple, nous pourrions simplement déplacer le 16 de l'autre côté de l'équation et diviser le tout par 400. C'est une méthode que nous avons déjà vue. Cependant, je veux vous montrer qu'il existe une autre manière de résoudre ce type d'équation, surtout si vous êtes à l'aise avec la factorisation.Factorisation
Supposons que nous ayons une équation de la forme \(4(x - 4) - 16 = 0\). Nous pouvons remarquer que -16 peut aussi être écrit comme \(4 \times 4\). Ainsi, nous pouvons factoriser par 4. Nous obtenons alors \(4(x - 4) + 4 \times 4 = 0\), ce qui peut être réécrit comme \(4(x - 4 + 4) = 0\). Nous nous retrouvons alors avec une équation de la forme \(a(bx + c) = 0\), comme nous l'avions prévu. Si nous avons quelque chose qui multiplie par 0, nous pouvons l'ignorer. Si cela n'est pas clair, divisez tout par 4. Nous obtenons alors \(x - 4 = 0\). En ajoutant 4 des deux côtés, nous trouvons que \(x = 4\). C'est la solution de notre équation.Conclusion
Il est important de noter que pour une équation de premier degré, il n'y aura toujours qu'une solution. Cependant, pour des équations de degré supérieur, il peut y avoir plusieurs solutions. En résumé, lorsque nous avons un produit nul, c'est ce qui est entre les parenthèses qui doit être nul. C'est là que nous trouvons la valeur de l'inconnue \(x\). N'hésitez pas à faire des exercices pour vous entraîner et à nous retrouver pour une prochaine vidéo.Nouvelle recrue
Visiteur anonyme
0 pts