Livre
13. Reconnaître une fonction affine dans un Graphique
Conditions d'achèvement
Consulter
Exercice
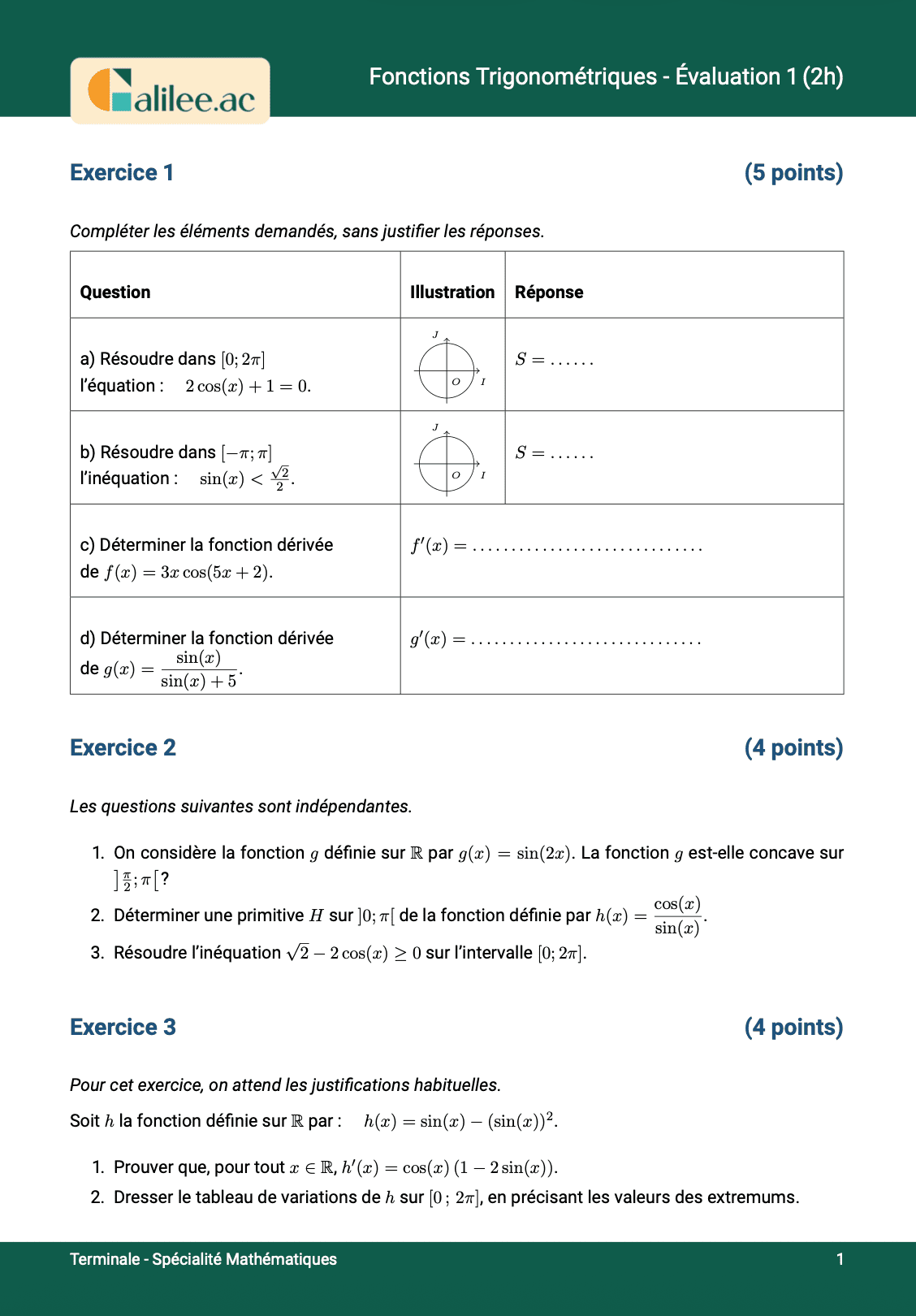
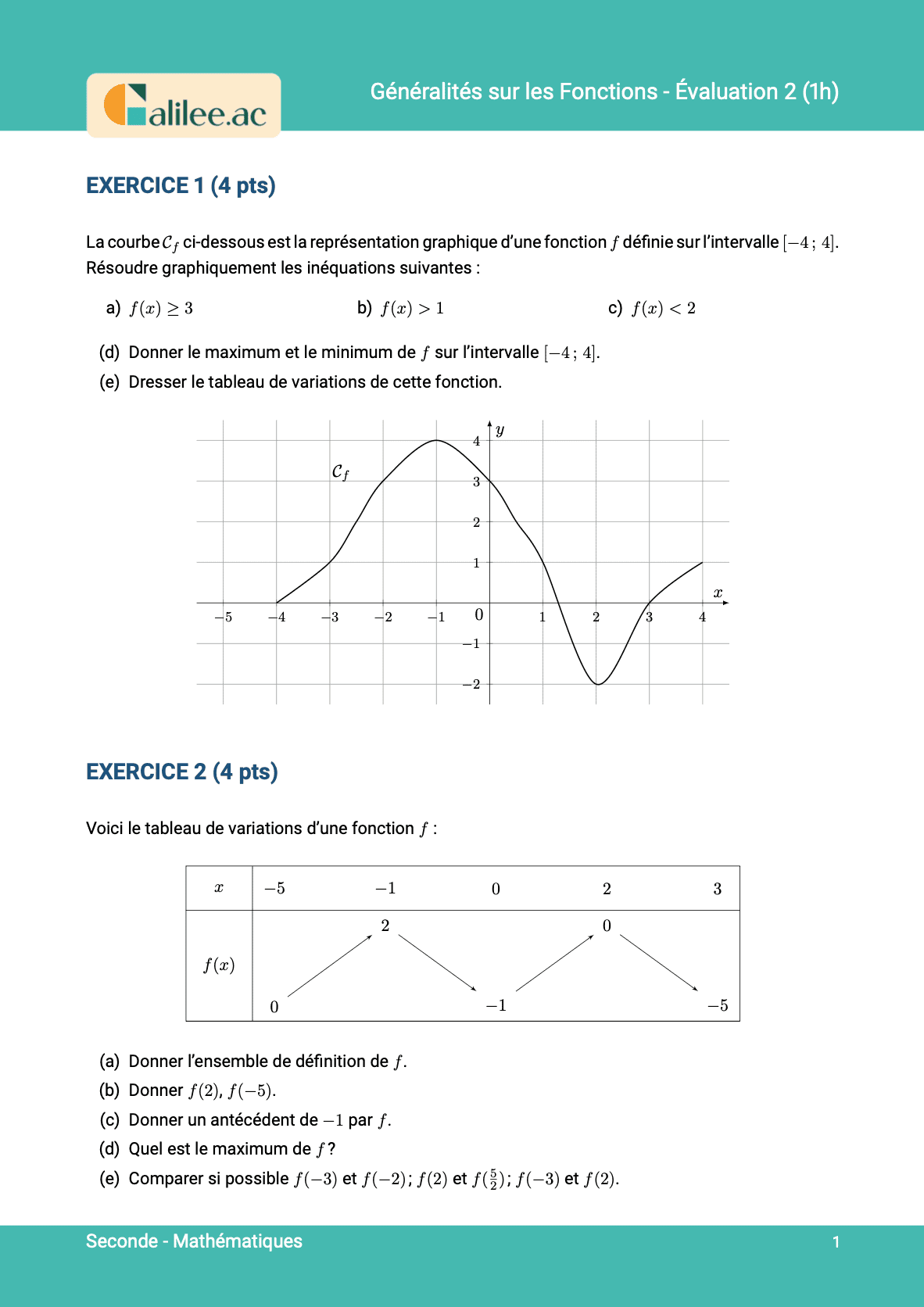
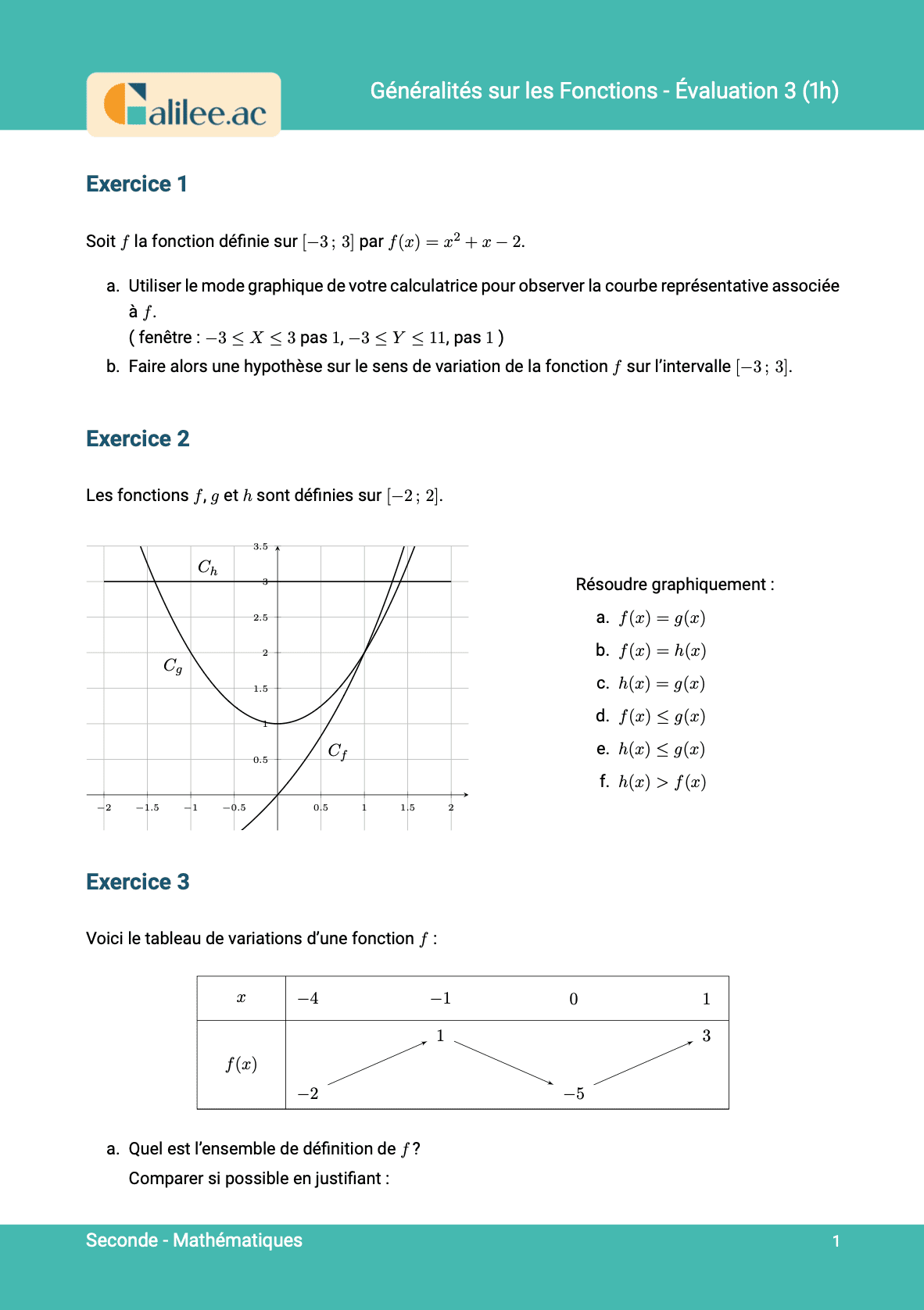
1
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allons-nous attaquer à un autre exercice : comment reconnaître des fonctions affines, cette fois-ci avec des graphiques. Nous allons nous appuyer sur la vidéo précédente qui traitait de la fonction affine. Son expression est \(f(x) = ax + b\), avec \(a\) et \(b\) qui sont des valeurs numériques. Ces valeurs peuvent être n'importe quel nombre que vous connaissez, cela peut être même la racine de 4, des fractions, des non-négatifs, mais aussi des 0. Nous avons vu dans la vidéo précédente les cas où \(a\) ou \(b\) étaient des zéros. Ce qui va nous intéresser maintenant, c'est que les représentations graphiques des fonctions affines sont toujours des droites.Représentations graphiques des fonctions affines
Les représentations graphiques sont toujours sur un intervalle donné, c'est-à-dire qu'elles sont limitées dans l'espace. Les fonctions \(f(x)\) peuvent prendre n'importe quelle valeur, elles peuvent être très grandes (un milliard, 500 millions, \(10^{154}\)), mais nous ne pouvons pas tout représenter sur un graphique. Il faut garder en tête que cela continue à l'infini dans le sens positif et négatif. C'est une droite infinie. Il faut se dire que la représentation graphique s'arrête dans le cadre du graphique, mais toutes les droites, en fait toutes les représentations, ne s'arrêtent pas dans l'absolu. C'est juste la représentation qui est finie.Exemples de fonctions affines
Prenons quelques exemples. Nous avons des fonctions \(f\), \(g\), \(h\), \(i\), \(j\) et \(k\). Nous allons les analyser dans l'ordre et à chaque fois nous allons nous demander si c'est une fonction affine. - Pour \(f(x)\), c'est une droite, donc c'est une fonction affine. - Pour \(g(x)\), c'est une droite horizontale, donc c'est une fonction affine avec \(a = 0\). - Pour \(h(x)\), c'est une droite qui passe par l'origine, donc c'est une fonction affine avec \(b = 0\). - Pour \(i(x)\), ce n'est pas une droite mais une courbe, donc ce n'est pas une fonction affine. - Pour \(j(x)\), c'est une droite mais qui est cassée en deux, donc ce n'est pas une fonction affine. - Pour \(k(x)\), c'est une droite verticale, donc ce n'est pas une fonction affine. En conclusion, les seules droites acceptées comme fonctions affines sont celles qui sont continues, sauf celle qui est verticale. J'espère que c'est clair. Faites des exercices, entraînez-vous et à bientôt pour une nouvelle leçon.Nouvelle recrue
Visiteur anonyme
3 pts