📖 Fiche résumée

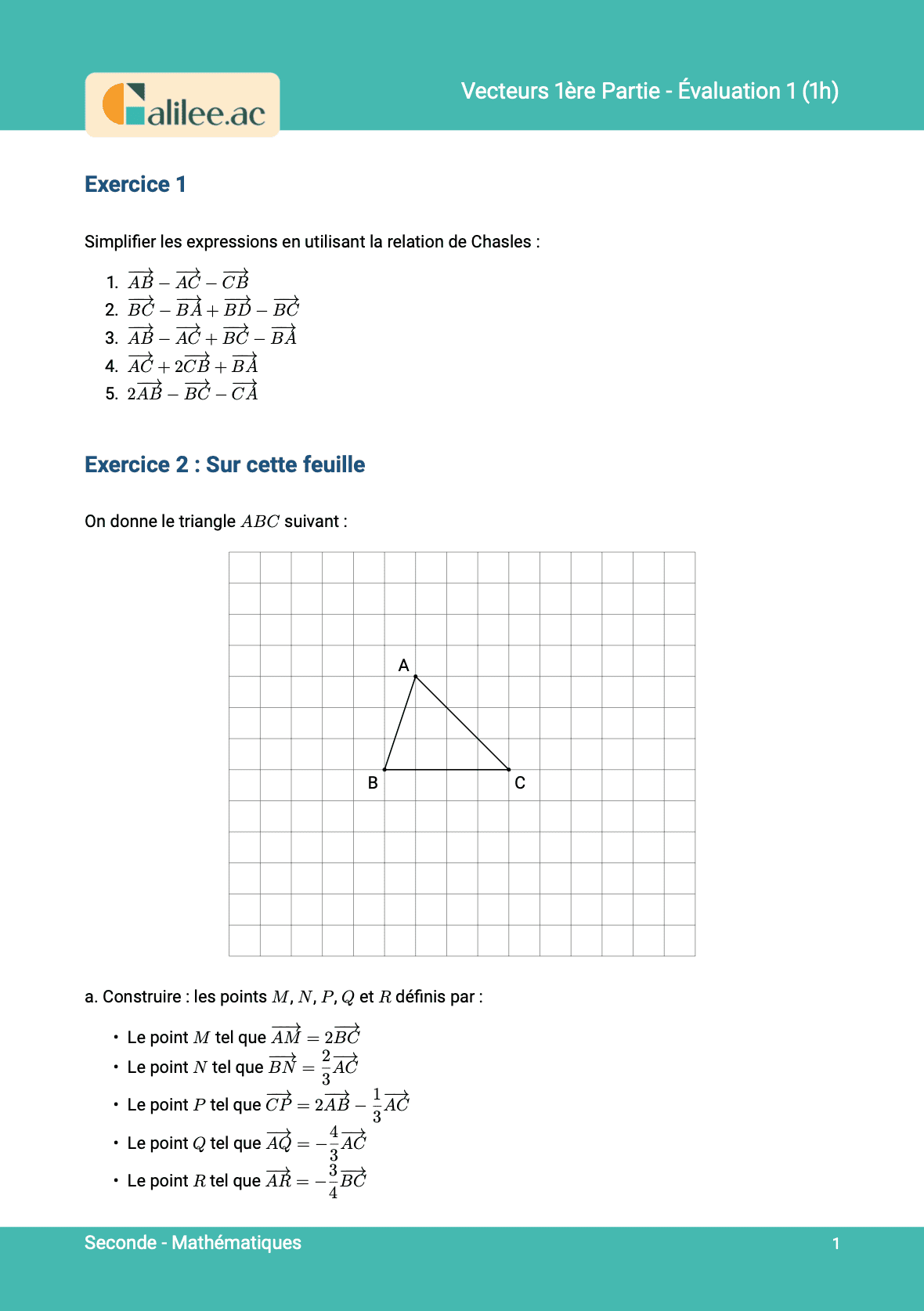
Introduction aux Vecteurs : Un Pilier des Mathématiques de Seconde

Le chapitre sur les vecteurs est une étape fondamentale du programme de mathématiques de la classe de Seconde. C'est un concept qui ouvre la porte à une nouvelle manière de penser la géométrie, non plus seulement avec des points, des droites et des angles, mais avec des objets qui encapsulent l'idée de déplacement. Les vecteurs sont essentiels non seulement en mathématiques pures, pour la géométrie analytique, mais aussi dans de nombreux domaines scientifiques comme la physique, où ils servent à modéliser des forces, des vitesses ou des accélérations. Cette fiche de cours a pour objectif de synthétiser les notions clés que tout élève de Seconde doit maîtriser. Nous aborderons la définition d'un vecteur, ses caractéristiques, comment le représenter et le manipuler dans un repère, les opérations de base comme l'addition vectorielle avec la relation de Chasles, et enfin, le concept crucial de colinéarité. Ce résumé vous fournira les bases solides nécessaires, mais n'oubliez pas que la pratique est la clé : consultez la fiche complète sur Galilee.ac pour des exemples détaillés et des exercices d'application.

Qu'est-ce qu'un vecteur ? Définition et caractéristiques

Définition intuitive d'un vecteur

Imaginez que vous vous déplacez d'un point A à un point B. Ce déplacement peut être décrit par un objet mathématique appelé vecteur, noté ������⃗. Un vecteur représente une translation, c'est-à-dire un glissement dans le plan ou dans l'espace sans rotation ni déformation. Il ne s'attache pas à une position précise ; le vecteur qui décrit le déplacement de Paris à Lyon est le même que celui qui décrit le déplacement de Bordeaux à Marseille, à condition que la distance, la direction et le sens soient identiques. Pour définir entièrement un vecteur, trois caractéristiques sont indispensables.

Les trois caractéristiques fondamentales d'un vecteur

Un vecteur 𝒖𝒖�⃗ est entièrement défini par les trois éléments suivants :

• La direction : C'est la droite qui porte le vecteur. Par exemple, la direction d'un vecteur ������⃗ est la droite (AB). Deux vecteurs qui sont portés par des droites parallèles ont la même direction. On peut penser à la direction comme l'inclinaison de la route que l'on suit.
• Le sens : Une fois la direction fixée, il y a deux sens de parcours possibles. Pour le vecteur ������⃗, le sens est de A vers B. Le vecteur ������⃗ a la même direction que ������⃗ mais un sens opposé. Si la direction est la route, le sens est la destination que l'on choisit sur cette route.
• La norme : C'est la longueur du vecteur, c'est-à-dire la distance entre son point de départ et son point d'arrivée. La norme du vecteur ������⃗ est la longueur du segment [AB] et se note ‖������⃗‖. C'est une valeur toujours positive ou nulle. Un vecteur dont la norme est nulle est appelé le vecteur nul, noté �0⃗.

Représentation et calculs dans un repère orthonormé

Pour pouvoir effectuer des calculs, il est très pratique de travailler dans un repère du plan, généralement un repère orthonormé (O, I, J). Dans ce cadre, chaque point et chaque vecteur peuvent être décrits par des nombres : leurs coordonnées.

Calculer les coordonnées d’un vecteur

Soit deux points A et B dont les coordonnées sont respectivement A(𝒙𝒙𝑨𝑨 ; 𝒚𝒚𝑨𝑨) et B(𝒙𝒙𝑩𝑩 ; 𝒚𝒚𝑩𝑩). Le vecteur ������⃗ qui représente le déplacement de A à B a pour coordonnées la différence des coordonnées de ses points d'arrivée et de départ.

La formule est la suivante : ������⃗ (𝒙𝒙𝑩𝑩 − 𝒙𝒙𝑨𝑨 ; 𝒚𝒚𝑩𝑩 − 𝒚𝒚𝑨𝑨).

L'abscisse du vecteur est la différence des abscisses des points (arrivée moins départ), et son ordonnée est la différence des ordonnées. Ces deux nombres, 𝒙𝒙 = 𝒙𝒙𝑩𝑩 − 𝒙𝒙𝑨𝑨 et 𝒚𝒚 = 𝒚𝒚𝑩𝑩 − 𝒚𝒚𝑨𝑨, sont les composantes du vecteur. Elles indiquent le déplacement horizontal (x) et vertical (y) nécessaire pour aller de A à B.

Calcul de la norme d'un vecteur

Une fois que l'on connaît les coordonnées d'un vecteur 𝒖𝒖�⃗(𝒙𝒙 ; 𝒚𝒚), on peut facilement calculer sa norme (sa longueur) en utilisant une formule qui découle directement du théorème de Pythagore. Le déplacement horizontal x et le déplacement vertical y forment les deux côtés d'un triangle rectangle dont l'hypoténuse est le vecteur lui-même.

La formule de la norme est : ‖�𝒖𝒖⃗‖ = √ (𝒙𝒙² + 𝒚𝒚²).

Par exemple, si un vecteur a pour coordonnées (3 ; 4), sa norme sera √(3² + 4²) = √(9 + 16) = √25 = 5. Il est important de noter que la norme est toujours une valeur positive.

Coordonnées du milieu d'un segment

Les vecteurs sont intimement liés à la géométrie des points. Une formule très utile est celle qui permet de trouver les coordonnées du milieu d'un segment. Si I est le milieu du segment [AB], avec A(𝒙𝒙𝑨𝑨 ; 𝒚𝒚𝑨𝑨) et B(𝒙𝒙𝑩𝑩 ; 𝒚𝒚𝑩𝑩), alors ses coordonnées sont la moyenne des coordonnées des points A et B.

La formule pour les coordonnées de I est : 𝑰𝑰 ((𝒙𝒙𝑨𝑨 + 𝒙𝒙𝑩𝑩)/𝟐 ; (𝒚𝒚𝑨𝑨 + 𝒚𝒚𝑩𝑩)/𝟐).

Cette formule est essentielle pour résoudre de nombreux problèmes de géométrie, comme prouver qu'un quadrilatère est un parallélogramme en montrant que ses diagonales se coupent en leur milieu.

Opérations et relations vectorielles

Égalité de deux vecteurs et parallélogrammes

Deux vecteurs ������⃗ et ������⃗ sont dits égaux s'ils ont les mêmes caractéristiques : même direction, même sens et même norme. D'un point de vue analytique, cela signifie qu'ils ont exactement les mêmes coordonnées. Si 𝒖𝒖�⃗(𝒙𝒙 ; 𝒚𝒚) et 𝒗𝒗�⃗(𝒙𝒙′ ; 𝒚𝒚′), alors 𝒖𝒖�⃗ = 𝒗𝒗�⃗ si et seulement si x = x' et y = y'.

Cette notion a une conséquence géométrique très importante. Si l'on a la relation vectorielle ������⃗ = ������⃗, cela signifie que le déplacement de A vers B est identique au déplacement de D vers C. Cette configuration forme un parallélogramme ABCD. Attention à l'ordre des points : l'égalité ������⃗ = ������⃗ implique que le quadrilatère est ABDC et non ABCD.

Vecteurs opposés

Le vecteur opposé d'un vecteur 𝒖𝒖�⃗ est noté −𝒖𝒖�⃗. Il possède la même direction et la même norme que 𝒖𝒖�⃗, mais son sens est contraire. Par exemple, le vecteur ������⃗ est l'opposé du vecteur ������⃗ : on écrit ������⃗ = −������⃗. Si le vecteur 𝒖𝒖�⃗ a pour coordonnées (x ; y), alors son opposé −𝒖𝒖�⃗ a pour coordonnées (−x ; −y).

La relation de Chasles : l'addition de vecteurs

L'une des règles les plus célèbres et les plus utiles concernant les vecteurs est la relation de Chasles. Elle permet d'additionner des vecteurs. Pour tous points A, B et C du plan, on a la relation :

������⃗ + ������⃗ = ������⃗

Géométriquement, cela s'interprète comme la composition de deux déplacements. Faire le trajet de A à B, puis de B à C, revient au même que de faire le trajet direct de A à C. Le point B sert d'intermédiaire. Cette relation est fondamentale pour simplifier des sommes vectorielles et résoudre des problèmes géométriques complexes. En coordonnées, l'addition de vecteurs est très simple : si 𝒖𝒖�⃗(𝒙𝒙 ; 𝒚𝒚) et 𝒗𝒗�⃗(𝒙𝒙′ ; 𝒚𝒚′), alors le vecteur somme 𝒖𝒖�⃗ + 𝒗𝒗�⃗ a pour coordonnées (𝒙𝒙 + 𝒙𝒙′ ; 𝒚𝒚 + 𝒚𝒚′).

Colinéarité de deux vecteurs

Définition et critère de colinéarité

Deux vecteurs non nuls 𝒖𝒖�⃗ et 𝒗𝒗�⃗ sont dits colinéaires s'ils ont la même direction. Autrement dit, ils sont portés par des droites parallèles. Cette propriété peut être vérifiée de deux manières principales.

La première est la définition algébrique : 𝒖𝒖�⃗ et 𝒗𝒗�⃗ sont colinéaires s'il existe un nombre réel k tel que 𝒖𝒖�⃗ = k × 𝒗𝒗�⃗. Ce nombre k est le coefficient de proportionnalité entre les deux vecteurs. Si k > 0, les vecteurs ont le même sens. Si k < 0, ils ont des sens opposés. Si k = 0, alors 𝒖𝒖�⃗ est le vecteur nul.

Le déterminant : un outil puissant pour prouver la colinéarité

En classe de Seconde, on introduit un outil de calcul très efficace pour tester la colinéarité : le déterminant. Soient deux vecteurs 𝒖𝒖�⃗(𝒙𝒙 ; 𝒚𝒚) et 𝒗𝒗�⃗(𝒙𝒙′ ; 𝒚𝒚′). Leur déterminant se note det(𝒖𝒖�⃗, 𝒗𝒗�⃗) et se calcule avec la formule suivante, souvent appelée "produit en croix" :

det(𝒖𝒖�⃗, 𝒗𝒗�⃗) = 𝒙𝒙𝒚𝒚′ − 𝒚𝒚𝒙𝒙′

La propriété fondamentale est la suivante : deux vecteurs 𝒖𝒖�⃗ et 𝒗𝒗�⃗ sont colinéaires si et seulement si leur déterminant est égal à zéro. det(𝒖𝒖�⃗, 𝒗𝒗�⃗) = 0 ⇔ 𝒖𝒖�⃗ et 𝒗𝒗�⃗ sont colinéaires.

Cette méthode est rapide et systématique, évitant d'avoir à chercher le coefficient k. Elle est donc privilégiée dans les exercices.

Application géométrique de la colinéarité

La colinéarité des vecteurs est un concept central en géométrie analytique, car elle permet de traduire des propriétés géométriques en calculs. Ses applications principales sont :

• Démontrer l'alignement de points : Trois points A, B et C sont alignés si et seulement si les vecteurs ������⃗ et ������⃗ sont colinéaires. Il suffit alors de calculer det(������⃗, ������⃗) et de vérifier s'il est nul.
• Démontrer le parallélisme de droites : Deux droites (AB) et (CD) sont parallèles si et seulement si les vecteurs ������⃗ et ������⃗ sont colinéaires. Là encore, le calcul du déterminant permet de conclure.

Conclusion : Une base essentielle pour la suite

Ce tour d'horizon des vecteurs en classe de Seconde met en lumière les définitions et formules incontournables. De la simple définition d'un déplacement à l'outil puissant qu'est le déterminant, chaque élément de ce chapitre constitue un maillon essentiel pour votre réussite en mathématiques. Maîtriser les calculs de coordonnées, la norme, la relation de Chasles et le test de colinéarité vous donnera des bases solides pour aborder la géométrie de manière plus analytique et pour vous préparer aux chapitres futurs, notamment en Première avec le produit scalaire. Pour approfondir ces notions, découvrir des exemples concrets et vous entraîner avec des exercices corrigés, nous vous invitons à télécharger et consulter la fiche de cours complète disponible sur Galilee.ac.