📖 Fiche résumée

Introduction aux Polynômes du Second Degré

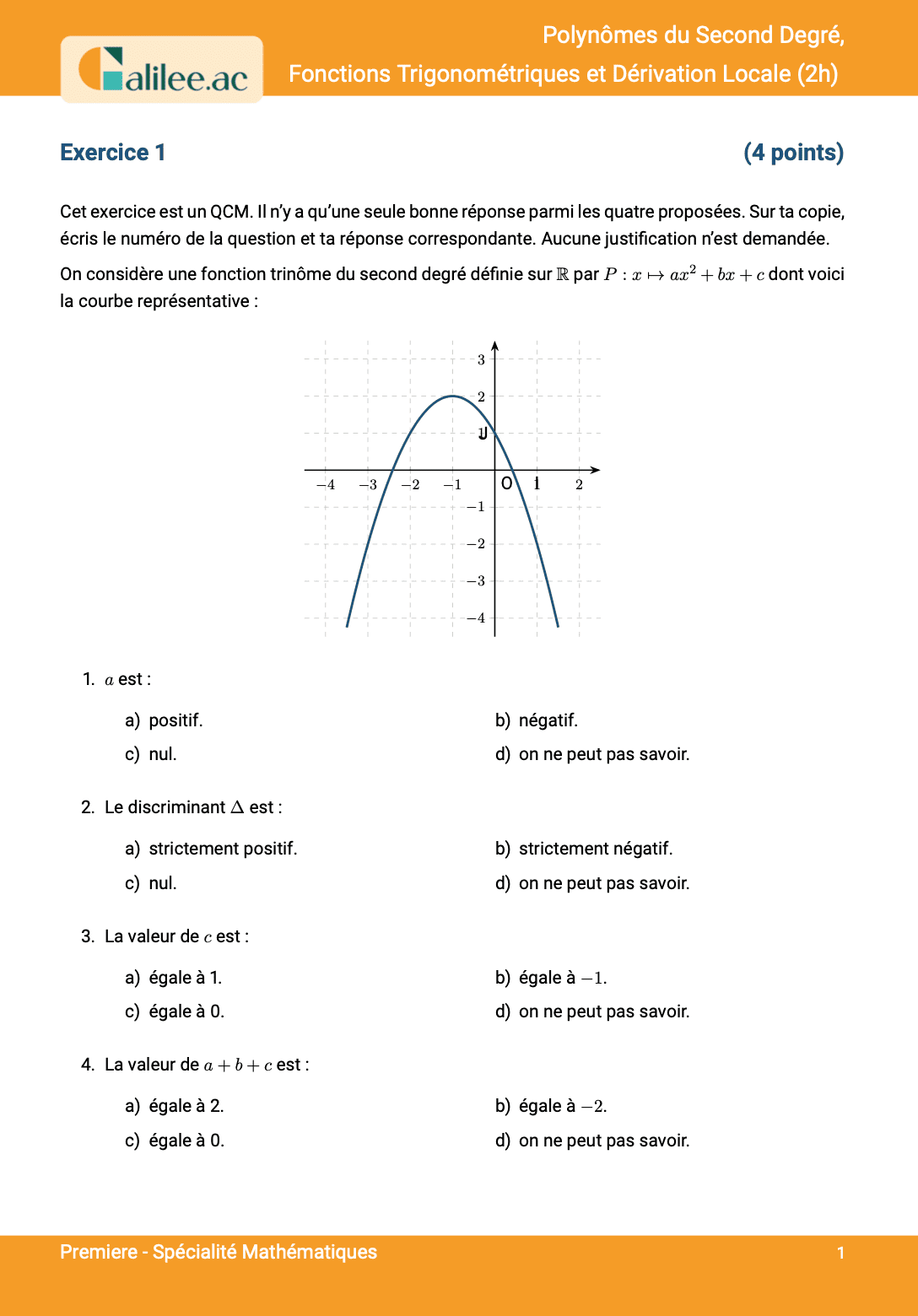
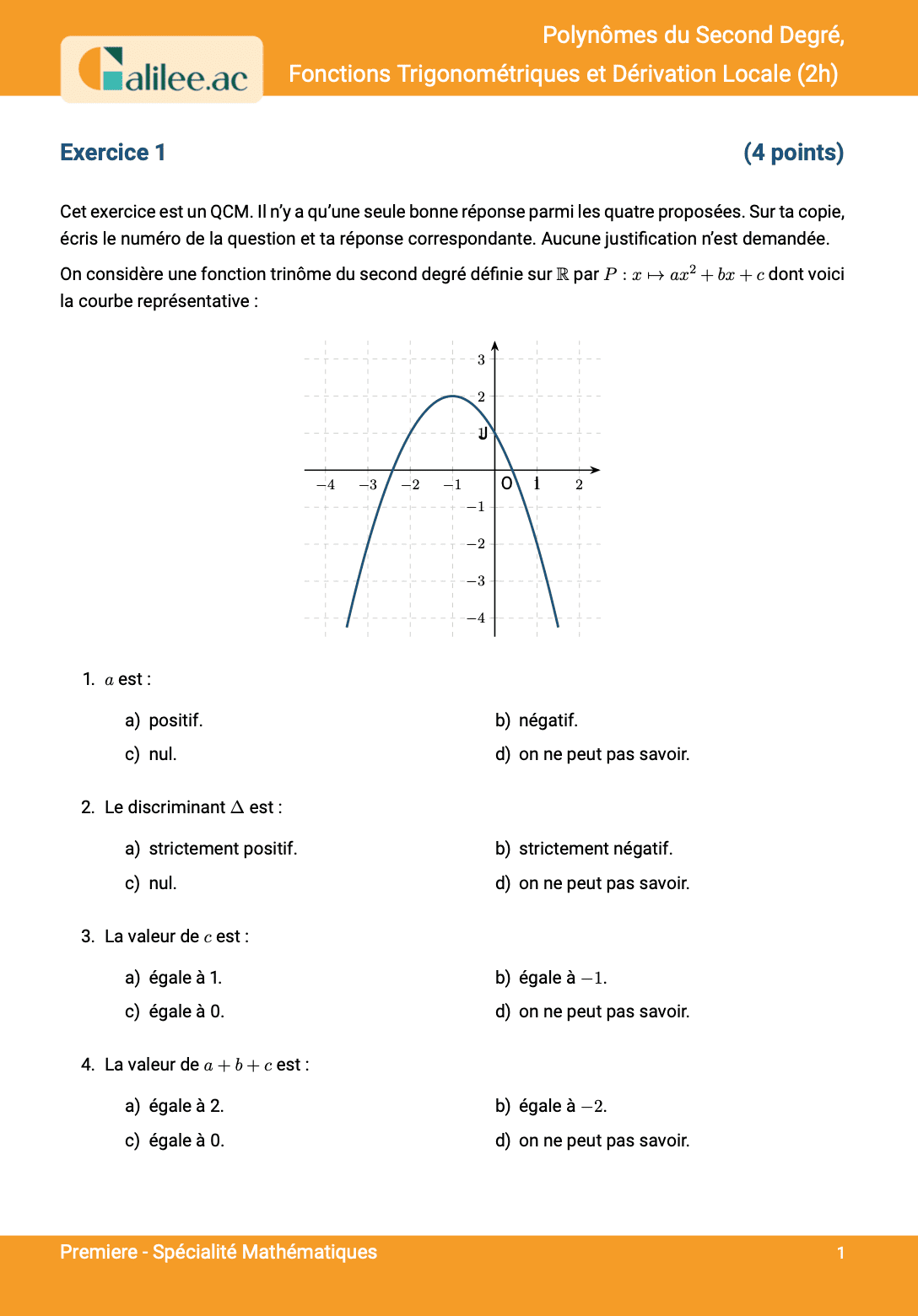
Les polynômes du second degré, également appelés trinômes du second degré, constituent un chapitre fondamental du programme de mathématiques de la classe de Première en spécialité. Leur maîtrise est indispensable non seulement pour la réussite de l'année, mais aussi pour aborder sereinement les études supérieures, notamment dans les domaines scientifiques. Une fonction polynôme du second degré est une fonction f définie sur l'ensemble des nombres réels ℝ par une expression de la forme f(x) = ax² + bx + c, où a, b, et c sont des coefficients réels et, condition essentielle, a ≠ 0. La représentation graphique de cette fonction est une courbe bien connue : la parabole.

Cette fiche de révision a pour objectif de synthétiser l'ensemble des connaissances et des savoir-faire relatifs à ce chapitre. Nous aborderons en détail les trois formes d'écriture d'un polynôme du second degré (développée, canonique, et factorisée), l'étude de ses variations, la méthode de résolution des équations du type ax² + bx + c = 0 grâce au discriminant, et enfin, l'étude du signe du polynôme. Chaque concept est illustré par les formules clés à retenir pour une compréhension complète.

Les Trois Formes d'un Polynôme du Second Degré

L'un des aspects les plus importants de ce chapitre est de savoir jongler entre trois écritures différentes du même polynôme. Chaque forme a son utilité et révèle des informations spécifiques sur la fonction et sa parabole représentative.

1. La Forme Développée : f(x) = ax² + bx + c

C'est la forme la plus courante et souvent le point de départ de l'analyse. Dans cette expression, a, b, et c sont des coefficients réels.

• Le coefficient a est le terme dominant. Son signe détermine l'orientation de la parabole : si a > 0, la parabole est tournée vers le haut ; si a < 0, elle est tournée vers le bas. Il est crucial de noter que a ne peut être nul, sinon l'expression deviendrait une fonction affine (bx + c).
• Le coefficient c est l'ordonnée à l'origine. C'est la valeur de f(0), qui correspond au point d'intersection de la parabole avec l'axe des ordonnées (l'axe y), de coordonnées (0, c).

Cette forme est particulièrement utile pour calculer rapidement des images et pour dériver la fonction.

2. La Forme Canonique : f(x) = a(x - α)² + β

La forme canonique est sans doute la plus puissante pour l'étude de la fonction. Elle met en évidence les caractéristiques géométriques de la parabole.

• Les coordonnées (α, β) représentent le sommet de la parabole.
• α (alpha) est l'abscisse du sommet. Il correspond également à l'axe de symétrie de la parabole, d'équation x = α. On le calcule à partir de la forme développée avec la formule : α = -b / (2a).
• β (beta) est l'ordonnée du sommet. C'est l'extremum (minimum ou maximum) de la fonction. On le calcule en évaluant la fonction en α : β = f(α). Si a > 0, β est le minimum de la fonction. Si a < 0, β est le maximum.

Grâce à la forme canonique, le tableau de variations de la fonction devient trivial à établir.

3. La Forme Factorisée : f(x) = a(x - x₁)(x - x₂)

Cette forme n'existe que si le polynôme admet au moins une racine réelle. Elle est directement liée aux solutions de l'équation f(x) = 0.

• x₁ et x₂ sont les racines du polynôme. Ce sont les valeurs de x pour lesquelles f(x) = 0.
• Graphiquement, les racines correspondent aux abscisses des points d'intersection de la parabole avec l'axe des abscisses (l'axe x).

La forme factorisée est donc idéale pour résoudre des équations et pour déterminer rapidement le signe du polynôme. La recherche de ces racines nous amène naturellement au concept du discriminant.

Résolution de l'équation ax² + bx + c = 0

Résoudre une équation du second degré est une compétence centrale. La méthode repose sur le calcul d'un nombre clé : le discriminant, noté delta (Δ).

Le Discriminant Δ = b² - 4ac

Le discriminant est calculé à partir des coefficients de la forme développée. Son signe nous renseigne sur le nombre de solutions réelles de l'équation f(x) = 0.

Étude des cas selon le signe de Δ

• Si Δ > 0 : L'équation admet deux solutions réelles distinctes, notées x₁ et x₂. Ces solutions, qui sont les racines du polynôme, sont données par les formules :
  x₁ = (-b - √Δ) / (2a) et x₂ = (-b + √Δ) / (2a).
  Dans ce cas, la parabole coupe l'axe des abscisses en deux points distincts, et la forme factorisée existe.
• Si Δ = 0 : L'équation admet une unique solution réelle, appelée racine double, notée x₀.
  Cette solution est donnée par la formule : x₀ = -b / (2a). On remarque que x₀ = α.
  Dans ce cas, le sommet de la parabole est situé sur l'axe des abscisses. La parabole est tangente à cet axe au point (x₀, 0). Le polynôme peut se factoriser sous la forme f(x) = a(x - x₀)².
• Si Δ < 0 : L'équation n'admet aucune solution dans l'ensemble des nombres réels.
  Il n'existe pas de valeur de x réelle pour laquelle f(x) = 0. Graphiquement, la parabole ne coupe jamais l'axe des abscisses. Elle est située entièrement au-dessus (si a > 0) ou entièrement en dessous (si a < 0) de cet axe. Le polynôme ne peut pas être factorisé dans ℝ.

Étude des Variations et de l'Extremum

L'étude des variations d'un polynôme du second degré est simple une fois que l'on connaît le signe de a et les coordonnées du sommet (α, β).

• Si a > 0 : La fonction est d'abord décroissante sur l'intervalle ]-∞, α], puis croissante sur l'intervalle [α, +∞[. Elle admet un minimum global en x = α, et ce minimum vaut β.
• Si a < 0 : La fonction est d'abord croissante sur l'intervalle ]-∞, α], puis décroissante sur l'intervalle [α, +∞[. Elle admet un maximum global en x = α, et ce maximum vaut β.

Ces informations sont synthétisées dans un tableau de variations, un outil visuel essentiel pour résumer le comportement de la fonction.

Signe du Polynôme

Déterminer le signe de f(x) = ax² + bx + c consiste à trouver sur quels intervalles f(x) est positif, négatif ou nul. La règle dépend, encore une fois, du signe du discriminant Δ et du signe de a.

• Si Δ > 0 (deux racines x₁ et x₂) : Le polynôme est du signe de a à l'extérieur des racines (pour x ∈ ]-∞, x₁[ ∪ ]x₂, +∞[) et du signe de -a entre les racines (pour x ∈ ]x₁, x₂[). Il s'annule en x₁ et x₂.
• Si Δ = 0 (une racine double x₀) : Le polynôme est toujours du signe de a, sauf en x₀ où il s'annule.
• Si Δ < 0 (pas de racine réelle) : Le polynôme est toujours du signe de a sur l'ensemble des réels ℝ.

Ces règles se retiennent facilement et permettent de construire un tableau de signe complet, indispensable pour la résolution d'inéquations.

Relations entre Coefficients et Racines

Lorsque le polynôme admet deux racines x₁ et x₂ (cas Δ ≥ 0), il existe des liens utiles entre ces racines et les coefficients a, b, c :

• Somme des racines (S) : x₁ + x₂ = -b/a
• Produit des racines (P) : x₁ * x₂ = c/a

Ces formules permettent de vérifier la validité de racines que l'on a calculées ou de trouver une racine si l'autre est évidente (par exemple, si 1 est une racine, alors l'autre est P).

Conclusion : Une Synthèse Essentielle

Les polynômes du second degré sont un pilier des mathématiques au lycée. Leur étude complète, des différentes formes à la résolution d'équations et à l'étude de signe, offre une boîte à outils puissante pour de nombreux problèmes. Chaque forme d'écriture apporte un éclairage unique : la forme développée pour les calculs de base, la forme canonique pour l'étude des variations et l'extremum, et la forme factorisée pour les racines et le signe. Le discriminant Δ reste la clé de voûte qui relie ces concepts. Pour une vision encore plus claire et une mémorisation efficace des formules et des représentations graphiques, n'hésitez pas à consulter la fiche de cours complète qui résume visuellement tous ces éléments indispensables à votre réussite.