Livre
6. Calculer l'aire entre deux fonctions
Conditions d'achèvement
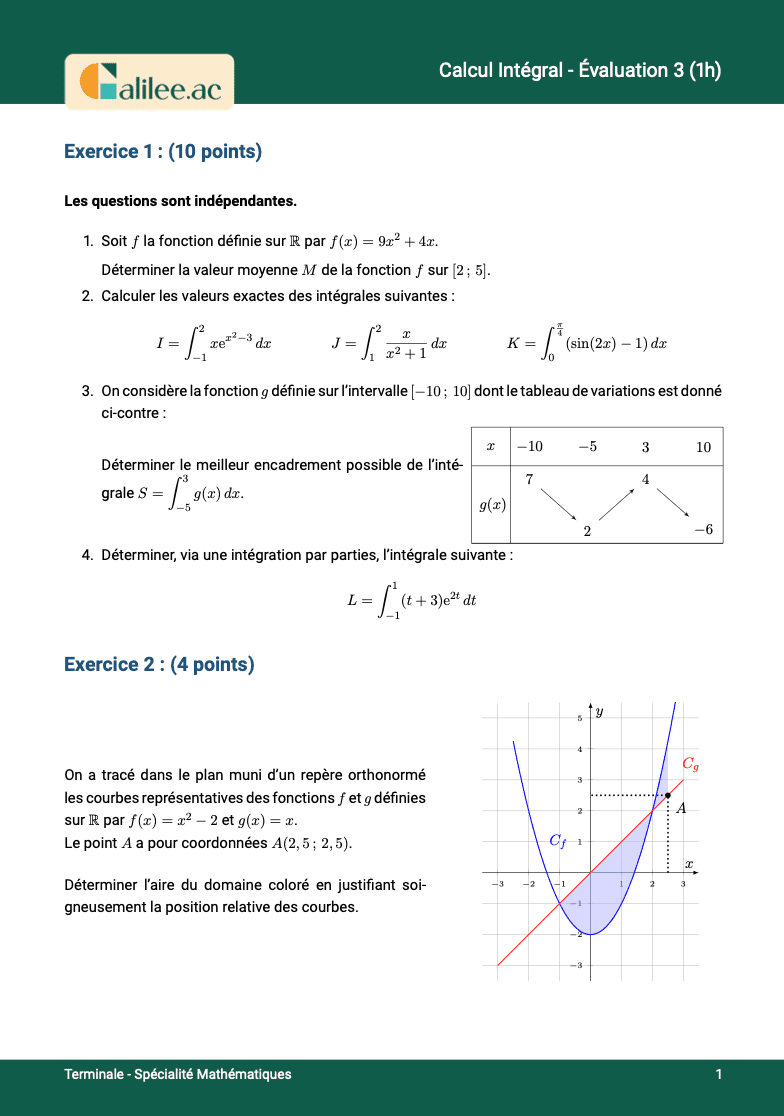
Exercice
1
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour voir une compétence classique qui est un peu difficile mais pas trop : comment calculer l'aire entre deux courbes représentatives. On se fait ça tout de suite.Exercice
Je vous ai fait un exercice simple. Dans cet exercice, je vous donne la représentation de deux droites, une qui s'appelle \(f\), un polynôme du second degré, l'autre qui s'appelle \(g\), un polynôme du second degré. Je vous demande de me calculer l'aire qui est finalement comprise entre la courbe de \(f\) et la courbe de \(g\). Pour calculer l'aire comprise entre deux courbes, c'est l'intégrale entre le début et la fin de la plage rouge, donc ici entre 2 et 4, de la fonction au-dessus moins la fonction en dessous. La fonction au-dessus ici, c'est \(g(x)\) et la fonction en dessous ici, c'est \(f(x)\). Remarquez que j'aurais pu compliquer beaucoup l'exercice en enlevant les chiffres 2 et 4 et du coup vous vous seriez demandé mais entre quoi et quoi est-ce que je dois faire mon intégrale, autrement dit où est-ce que ça commence, où est-ce que ça se termine. Comment est-ce que je ferais ça ? Vous me diriez, je résous l'équation \(f(x) = g(x)\), autrement dit \(-x^2 + 6x - 7 = x^2 - 6x + 9\).Résolution
Je suis un type extrêmement sympathique, je n'ai pas du tout envie de me taper une résolution de polynôme du second degré parce que finalement, comme tout mathématicien, j'ai la flemme. Du coup, je vous donne directement les bornes, vous devez faire votre calcul et ensuite on roule. On calcule notre intégrale. Comment est-ce qu'on peut le comprendre ce truc là, pourquoi est-ce qu'on fait la différence ? Regardez, finalement pour avoir l'aire en rouge, ce que je peux faire c'est calculer l'aire en bleu, c'est à dire l'aire sous la courbe de \(g\), et enlever l'aire en noir, c'est à dire cette zone là, c'est à dire l'aire sous la courbe de \(f\). Donc j'ai l'aire sous la courbe de \(g\) moins l'aire sous la courbe de \(f\) et on calcule. Ça me fait l'intégrale entre 2 et 4 de \(g(x) - f(x)\), donc \(-x^2 + 6x - 7 - f(x)\), donc \(-x^2 - 6x + 9\). Et là, il faut vraiment que vous compreniez que c'est extrêmement simple. Je vais le distribuer donc je vais changer tous les signes donc mon plus \(x^2\) va devenir moins \(x^2\) donc je vais avoir \(-x^2 - x^2 = -2x^2\). Ensuite \(6x - 6x = 0\). Enfin, \(-7 - 9 = -16\). Maintenant, qu'est-ce que je fais ? Je sais que l'intégrale d'une fonction en fonction de \(x\) c'est une primitive de la fonction. Donc une primitive de cette fonction-là c'est \(-2x^3/3 + 6x^2 - 16x\). Une fois que c'est fini, je vais tout simplement appliquer cette fonction en 4 et lui enlever cette fonction en 2. Ce que je vous propose, c'est que je me le calcule tranquillement à la calculatrice. Donc, \(-32/3\) pour cette fonction-là appliquée en 4. Comment est-ce que j'ai fait le calcul ? J'ai juste remplacé le \(x\) qui est là par 4. Et je recommence pour l'avoir en 2. Cette fonction appliquée en 2, ça me fait \(-24\). Mais je veux faire moins la fonction appliquée en 2 donc \(-(-24)\) et j'ai plus qu'à mettre tout ça au même dénominateur. \(24 - 32/3\) ça me fait \(24/3 - 32/3\) et ça me fait un total de \(40/3\). Si mes calculs sont bons, les calculs sont bons. On a bien une aire positive. L'aire qui est là, elle fait \(40/3\), donc à peu près 13,33. On vous a mis des petits exercices en dessous, entraînez-vous. Ça, pour le coup, ça tombe au contrôle, ça tombe au bac. À vous de jouer, vous êtes des champions.Nouvelle recrue
Visiteur anonyme
0 pts