Livre
9. Dériver avec ln
Conditions d'achèvement
Exercice
1
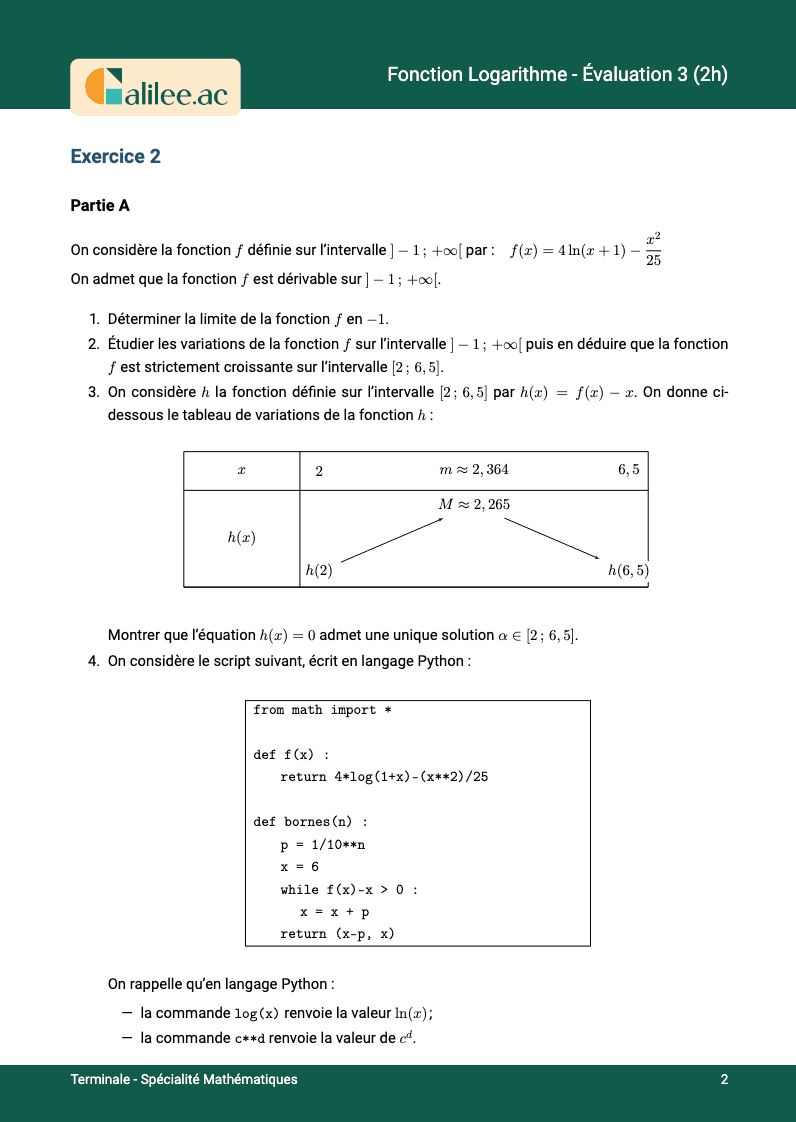
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
PremièreRecommandé
Contrôle Fonction ln - sujet 3
Chapitres: Fonction logarithme
Terminale spécialitéRecommandé
Contrôle Fonction ln - sujet 2
Chapitres: Fonction logarithme
Terminale spécialitéRecommandé
Contrôle logarithme népérien difficile
Chapitres: Continuité et étude de fonctions Dérivation et convexité ...
Pareil pour moi, 4eme fois que je réesaye et j'ai toujours une erreur
Pareil Impossible d'avoir la correction de l'exercice 4
Impossible d'avoir la correction de l'exercice 4 . Est-ce normal ?
Non ce n'est pas normal, actualise la page !!
Si çà ne marche toujours pas envoie nous une capture d'écran
Si çà ne marche toujours pas envoie nous une capture d'écran
Il n'y aurait pas par hasard un problème de signe dans l'exercice 3 ?
Bonjour @angelangel
Bon retour parmi nous, cela faisait un bye 😊😊😊 !!
Merci de nous avoir mentionné le problème, cela a été corrigé et tu peux réessayer !!
Bon retour parmi nous, cela faisait un bye 😊😊😊 !!
Merci de nous avoir mentionné le problème, cela a été corrigé et tu peux réessayer !!
Introduction
Allez les amis, on est parti pour une compétence uniquement composée de plaisir à prendre à dériver avec logarithme. Vous avez besoin de deux formules : 1. La dérivée de \(\ln(x)\) est \(\frac{1}{x}\). C'est plus compliqué que l'exponentielle mais ça reste quand même facile à retenir. 2. La dérivée de \(\ln(u(x))\), c'est-à-dire \(\ln\) d'une fonction, est \(\frac{u'}{x}\).Exemple de dérivation
Prenons l'exemple de la fonction \(f(x) = x \ln(x) - x\). La dérivée de \(x\) est 1 et la dérivée de \(\ln(x)\) est \(\frac{1}{x}\). Cependant, la dérivée de \(x \ln(x)\) n'est pas simplement \(1 \times \frac{1}{x}\). Ce qu'on a ici, c'est une multiplication de deux fonctions, \(u(x) = x\) et \(v(x) = \ln(x)\). La dérivée de \(u(x)v(x)\) est \(u'(x)v(x) - u(x)v'(x)\). Donc, pour trouver \(f'(x)\), on va appliquer cette formule.Calcul de la dérivée
On a donc \(f'(x) = u'(x)v(x) - u(x)v'(x) - 1\). En remplaçant \(u'(x)\) par 1, \(v(x)\) par \(\ln(x)\), \(u(x)\) par \(x\) et \(v'(x)\) par \(\frac{1}{x}\), on obtient \(f'(x) = 1 \times \ln(x) - x \times \frac{1}{x} - 1\). Cela simplifie à \(\ln(x) + 1 - 1\), soit simplement \(\ln(x)\).Interprétation du résultat
On voit donc que la dérivée de \(x \ln(x) - x\) est \(\ln(x)\). Cela signifie que la fonction \(x \ln(x) - x\) est une primitive de \(\ln(x)\), c'est-à-dire une fonction qui, lorsqu'on la dérive, donne \(\ln(x)\). C'est un concept important qui sera développé dans le prochain chapitre.Autre exemple de dérivation
Prenons maintenant la fonction \(u(x) = x^2 - 2x + 1\). Sa dérivée est \(u'(x) = 2x - 2\). Si on dérive \(\ln(u(x))\), on utilise la formule \(\frac{u'(x)}{u(x)}\), ce qui donne \(\frac{2x - 2}{x^2 - 2x + 1}\).Conclusion
Voilà, vous avez maintenant une bonne base pour dériver des fonctions avec des logarithmes. N'hésitez pas à vous entraîner avec des exercices pour bien maîtriser ces concepts.Nouvelle recrue
Invité
0 pts
