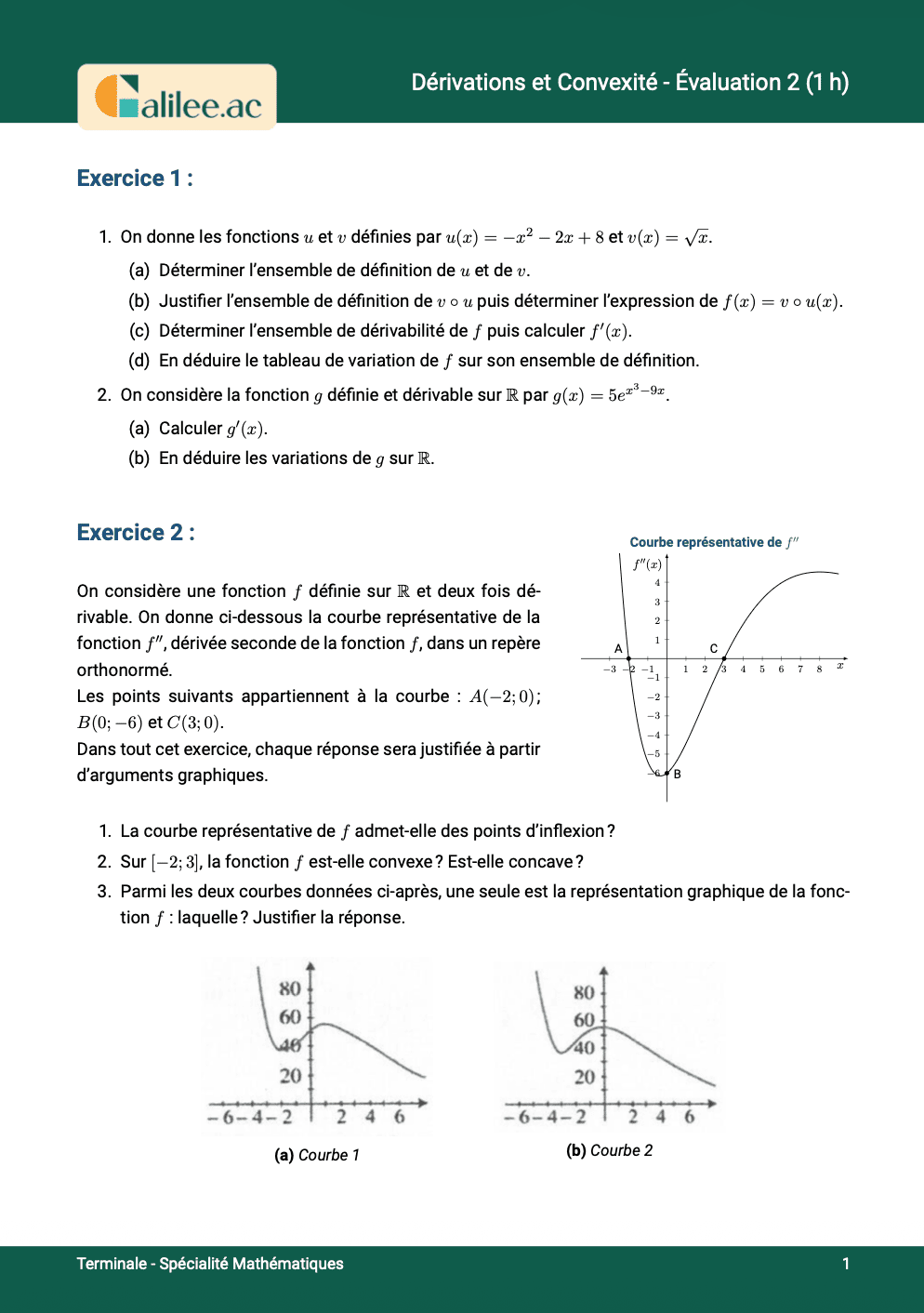
Livre
9. Tableau de variations avec la fonction inverse
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on continue notre épopée des tableaux de variation. Cette fois-ci, nous allons voir comment faire un tableau de variation en terminale quand on a une fonction inverse. Comme d'habitude, dès que vous devez faire un tableau de variation, dès que vous devez étudier les variations d'une fonction, c'est toujours les mêmes trois étapes : première étape, je dérive ; deuxième étape, j'étudie le signe de la dérivée ; et troisième étape, quand la dérivée est positive, ça monte, quand la dérivée est négative, ça descend. Je résume tout ça avec un tableau de variation où il y a toutes les informations et éventuellement les limites et les valeurs interdites.Première étape : la dérivation
On commence par la première étape, je dérive donc ma fonction \(f(x) = 2/x^2\). Je vous rappelle, et ça commence à faire plusieurs fois que je le dis, que dériver cette fonction, c'est quasiment comme dériver \(2 \times 1/x^2\). Quand vous dérivez \(f(x) = 2/x^2\), vous obtenez \(f'(x) = -4x/(x^2 - 1)^2\).Deuxième étape : étude du signe de la dérivée
Maintenant, on passe à la deuxième étape, l'étude du signe de la dérivée. Pour faire le tableau de signe de la dérivée, je vais pouvoir me contenter de faire un tableau avec le numérateur, soit \(-4x\), et avec le dénominateur, soit \(x^2 - 1\).Troisième étape : tableau de variation
Enfin, on arrive à la troisième étape, le tableau de variation de \(f(x) = 2/x^2\). Le domaine de définition de cette fonction est tout l'ensemble des réels sauf 1 et -1. On peut donc construire le tableau de variation en prenant en compte les limites de la fonction aux bornes du domaine de définition et aux points où la dérivée s'annule ou n'est pas définie. En résumé, la difficulté dans cet exercice est de comprendre que quand on a un produit ou un quotient, les zéros du numérateur et du dénominateur vont donner respectivement des zéros et des valeurs interdites dans le tableau de signe de la dérivée.Nouvelle recrue
Visiteur anonyme
2 pts