Livre
19. Asymptotes obliques
Conditions d'achèvement
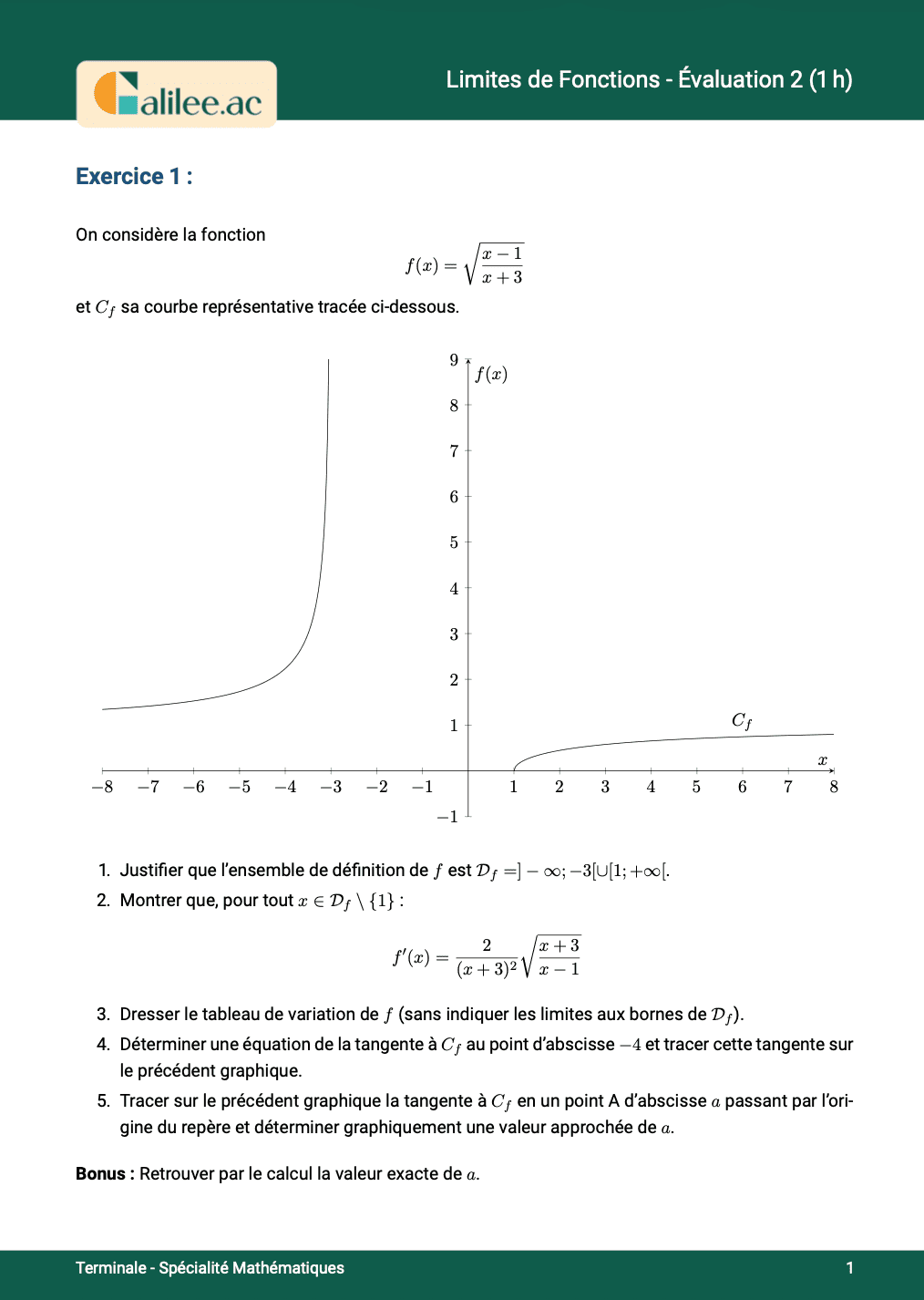
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour voir en 3 minutes comment démontrer qu'une fonction admet une asymptote oblique. On s'y met tout de suite.Définition d'une asymptote oblique
Une fonction admet une asymptote oblique si cette fonction va se rapprocher indéfiniment d'une droite d'équation \(y = ax + b\), qui est une asymptote oblique, par opposition aux asymptotes horizontales et verticales. Donc une fonction va admettre cela comme une asymptote si elle vient se rapprocher de cette droite à l'infini. Autrement dit, si la distance entre la fonction et cette droite tend vers zéro lorsque \(x\) tend vers l'infini.Démonstration
Si on note \(f(x)\) la fonction et \(y = ax + b\) la droite, on veut que l'écart entre ces deux tende vers zéro. Donc en fait, on veut que la limite de \(f(x) - (ax + b)\) soit égale à zéro. Parce que quand elle est égale à zéro, cela signifie que la fonction se rapproche indéfiniment de la droite. Donc on cherche à démontrer que la limite de \(f(x) - (ax + b)\) est égale à zéro. Prenons par exemple la fonction \(f(x) = -3x^2 + 2x + 1\), et supposons que notre asymptote soit \(y = ax + b = -3x + 2\). On cherche donc à démontrer que la limite de \(f(x) - (-3x + 2)\) est égale à zéro quand \(x\) tend vers l'infini. Pour cela, on va tout mettre au même dénominateur, c'est-à-dire \(x\). Cela nous donne la limite quand \(x\) tend vers l'infini de \(-3x^2/x + 2x/x - (-3x/x + 2/x)\). En simplifiant, on obtient la limite quand \(x\) tend vers l'infini de \(-3x + 2 - 3 + 2/x\). On veut montrer que cette limite est égale à zéro. Or, la limite quand \(x\) tend vers l'infini de \(1/x\) est bien zéro. Donc la limite de \(f(x) - (ax + b)\) est bien égale à zéro. Cela démontre que la droite \(y = -3x + 2\) est bien une asymptote oblique à la fonction \(f(x) = -3x^2 + 2x + 1\).Conclusion
Voilà, vous avez maintenant une méthode pour démontrer qu'une fonction admet une asymptote oblique. N'hésitez pas à faire des exercices pour vous entraîner, notamment des variations où l'on vous demande de trouver la valeur du nombre \(a\) ou \(b\) de l'asymptote. Bon courage, vous êtes des champions !Nouvelle recrue
Visiteur anonyme
0 pts