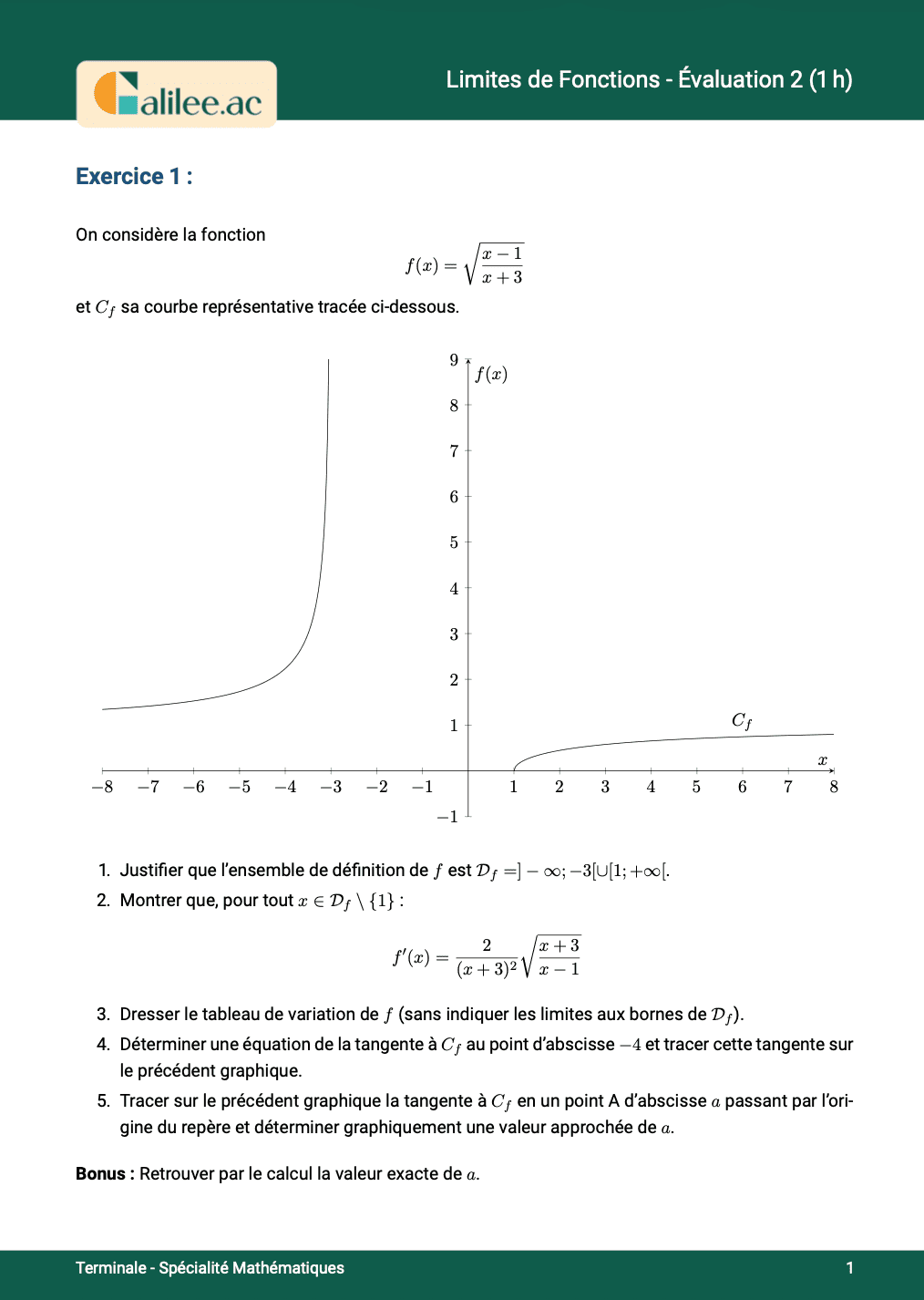
Livre
16. Limites : faire un tableau complet
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour voir comment les calculs de limite nous permettent de faire des tableaux de variation complet. On se fait ça tout de suite. Une fonction \(f(x)\), vous devez dresser son tableau de variation.Étape 1 : Étude du domaine de définition
Première étape, je vais étudier son domaine de définition si vous n'êtes pas donné dans l'énoncé. Donc le domaine de définition ici c'est a priori tout sauf ce qui pourrait annuler \(x - 2\) parce que comme on l'a vu dans cette vidéo, le domaine de définition d'une fonction quotient, en haut il y a aucun problème, en bas par contre faut que ça soit différent de 0. Donc il faut absolument que \(X\) soit différent de deux parce que quand \(X\) est égal à 2, \(x - 2\) ça fait 0, donc on prend le risque de diviser par 0. Donc finalement on veut tout donc \(R\) sauf ce nombre là qui peut nous embêter qui est 2. Donc on va enlever deux de \(R\) donc de moins l'infini jusqu'à 2 exclu puis de 2 jusqu'à plus l'infini.Étape 2 : Calcul de la dérivée et étude du signe
Ensuite, pour avoir le tableau de variation, première étape je dérive, deuxième étape j'étudie ici de la dérivée, troisième étape je mets les flèches. On va voir en quoi les limites vous permettent de faire la quatrième étape. Donc moi je vais dériver \(f(x)\) donc \(f'(x)\) c'est de la forme \(U / V\) donc ça va me faire \(U'V - UV' / V^2\). Donc \(U' = 2x + 2\), \(V = x - 2 - 1\), donc \(x^2 + 2x - 4x\), \(V = 1 / (x - 2)^2\) et ça me fait donc \(2x^2 - 4x + 2x - 4 - x^2 - 2x + 4\). Donc j'ai les quatre là et là qui vont s'enlever, \(2x^2 - x^2\) ça me fait \(x^2 - 2x - 2x - 4x / (x - 2)^2\) et vu que moi mon but ça va être d'étudier le signe de ça, je vais le factoriser autant que je peux donc je vais dire que c'est en haut \(x(x - 4) / (x - 2)^2\). Donc ma dérivée je peux la noter ici c'est \(f'(x) = x(x - 4) / (x - 2)^2\).Étape 3 : Tableau de variation
Ensuite, je vais faire une ligne avec une ligne qui soit en 4 et une ligne et \(x - 2^2\) pour essayer d'étudier le signe de \(f'(x)\). Donc je fais un long tableau où je mets d'abord \(X\), ensuite je vais faire le premier bout donc le signe de \(X\), ensuite le signe de \(x - 4\) et ensuite le signe de \(x - 2^2\). Je commence par mettre les valeurs importantes, \(x\) ça va s'annuler quand \(x\) vaut 0 donc ici je vais avoir un zéro, \(x - 2\) ça va quand \(x\) vaut 2 donc là je vais avoir un 0, ou là attention ici je vais avoir un zéro et \(X - 4\) ça va s'annuler quand \(x = 4\) donc ici je vais avoir un 0. Ensuite je réfléchis, \(x\) c'est une fonction croissante donc avant de valoir 0 elle est négative et ensuite elle est positive, \(x - 4\) elle est croissante donc avant de valoir 0 elle est négative et ensuite elle est positive et enfin \(x - 2\) elle est croissante des croissante c'est une fonction polynôme du second degré avec \(A\) qui est positif du coup elle va être positive et positif de toute façon à quelque chose au carré c'est forcément positif.Étape 4 : Calcul des limites
Maintenant je peux mettre \(F'x\) qui vaut donc divisé par ça donc les 0 duo ils vont rester des 0 c'est à dire que quand \(x\) vaut 0 tout s'annule quand \(x - 4\) vaut 0 tout s'annule attention quand \(x - 2\) vaut 0 on divise par 0 donc la valeur qui annule \(x - 2^2\) cette valeur là elle va donner lieu à une valeur interdite aussi bien pour la dérivée que pour la fonction vu que la fonction on a dit qu'elle était pas définie pour \(x = 2\). Pour le reste à faire 1-0 à 0 ensuite règle des signes moins par moins par plus moins plus par moins par plus moins plus par moins par plus moins et plus par plus par plus plus donc notre fonction on sait qu'elle va être moins par moins par plus plus et évidemment dans un peu plus avec plus donc elle va être tac décroissant et puis croissante. Ok, je vais mettre les valeurs ici donc ici ça va être la ligne de \(F\) donc je vais mettre \(F0\) facile, \(f2o\) ça me fait zéro plus zéro - 4 sur - 2 donc ça fait -4 sur -2 ça me fait 2 et en 4 ça va me faire 16 + 84 - 4 20 sur 2 donc là 10 et j'ai fini en première votre tableau vous l'aviez fini comme ça sauf que maintenant vous vous allez pouvoir rajouter tout ce qu'il y a ici ici ici ici et ici et je vais même vous dire quelque chose il faut absolument en terminale rendre un tableau de variation complet c'est à dire avec toutes les cases remplies y compris les potentiels limites donc là vous avez une deux trois quatre limites qui correspondent à les possibilités de votre domaine de définition vu qu'on a dit que c'était air privé de 2 les cas limite possible c'est soit moins l'infini celle qu'on retrouve ici soit plus l'infini celle qu'on retrouve ici soit 2 en arrivant par la gauche tac soit 2 en arrivant par là et on a bien une deux trois quatre limites qui correspondent à une deux trois quatre limites des bornes de noms de domaine de définition donc vous allez vous calculer ces quatre limites vous les faites comme vous voulez moi je vous donne la réponse ici entraînez-vous ici on va descendre vers moi l'infini là on va remonter vers plus l'infini là on va remonter vers plus l'infini et là on va descendre vers moins l'infini et là vous avez fini votre tableau de variation c'est un vrai tableau de variation de terminale où on a mis toutes nos limites on vous en a mis en dessous entraînez-vous vous avez des champions à vous de jouer.Caporal
Visiteur anonyme
32 pts