Livre
14. Limites : taux de variation caché
Conditions d'achèvement
Exercice
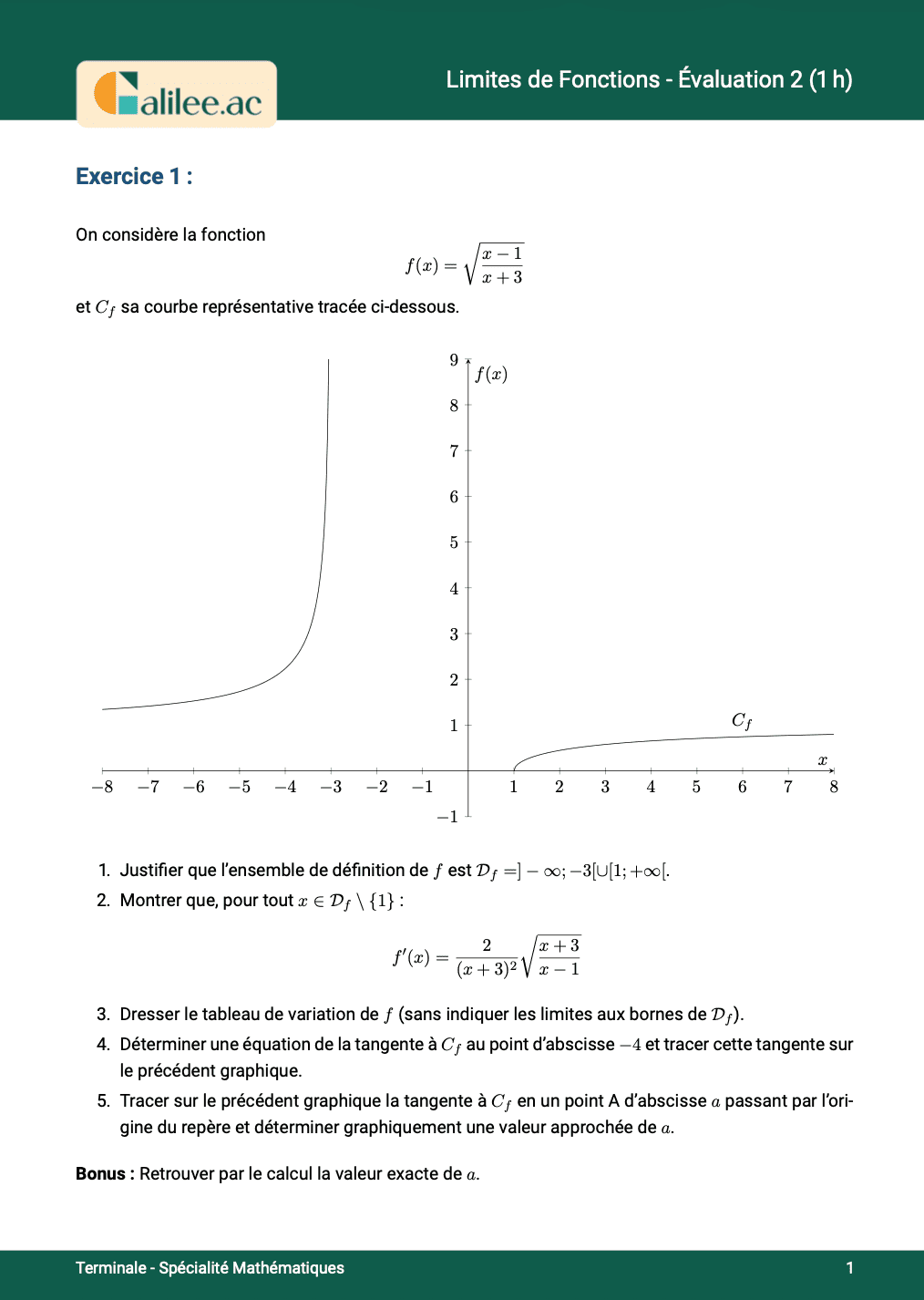
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Terminale spécialitéRecommandé
Contrôle Limites de Fonctions et Positions Relatives dans l'Espace
Chapitres: Vecteurs, droites et plans Représentations paramétriques et Équations cartésiennes ...
Terminale spécialitéRecommandé
Contrôle Etudes Suites, Fonctions, Dénombrement, Position Relative Espace
Chapitres: Étude de suites Dénombrement ...
Terminale spécialitéRecommandé
BAC BLANC - sujet 7
Chapitres: BAC BLANC Terminale Représentations paramétriques et Équations cartésiennes ...
Terminale spécialitéRecommandé
Contrôle Probabilités, Etudes de Fonctions et Suites, Géométrie dans l'Espace
Chapitres: Récurrence Étude de suites ...
Terminale spécialitéRecommandé
Contrôle Limites, suites et dénombrement - sujet 14
Chapitres: Limites de fonctions Récurrence ...
Terminale spécialitéRecommandé
Contrôle Dénombrement, limites et convexité - sujet 30
Chapitres: Dénombrement Limites de fonctions ...
Terminale spécialitéRecommandé
Contrôle Géométrie dans l'espace et logarithme - sujet 23
Chapitres: Vecteurs droites et plans ...
Terminale spécialitéRecommandé
Contrôle Fonctions, produit scalaire et espace - sujet 22
Chapitres: Limites de fonctions Continuité et étude de fonctions ...
Terminale spécialitéRecommandé
Contrôle Loi binomiale et limites de fonctions - sujet 29
Chapitres: Loi binomiale Limites de fonctions
Terminale spécialitéRecommandé
BAC BLANC - sujet 11
Chapitres: BAC BLANC Terminale Probabilités Conditionnelles ...
Terminale spécialitéRecommandé
Contrôle Limites de fonctions et loi binomiale - sujet 17
Chapitres: Limites de fonctions Loi binomiale
Terminale spécialitéRecommandé
Contrôle Loi Binomiale 2
Chapitres: Limites de fonctions
s'il vous plait pouvez vous me detailler le probleme numero 2 de l'exercice 3 ?
Bonjour @AboudramaneTraore
La correction du problème a été très bien détaillée, suivez cela de façon rigoureuse.
Bonne compréhension champion
La correction du problème a été très bien détaillée, suivez cela de façon rigoureuse.
Bonne compréhension champion
Introduction
Allons voir un petit cas particulier de calcul de limites qui est vraiment intéressant. C'est celui où on veut nous faire calculer des limites et nous montrer qu'il y a un taux de variation caché, qu'il y a un nombre dérivé qui est caché. C'est très amusant et instructif. En faisant cela, vous allez apprendre à les reconnaître. Il y en a aussi avec d'autres fonctions. Ce que nous allons utiliser, c'est la définition du nombre dérivé.Définition du nombre dérivé
Je vous rappelle la définition du nombre dérivé pour ceux qui ont oublié les calculs de première. La limite quand \(x\) tend vers \(a\) de \(\frac{f(x) - f(a)}{x - a}\). Pour des raisons pratiques, on avait préféré dire que c'était la limite quand \(h\) tend vers zéro de \(\frac{f(a + h) - f(a)}{h}\). Mais ce n'est pas cette définition que nous visons ici, c'est vraiment la première. Le nombre dérivé en \(a\) est la limite de \(\frac{f(x) - f(a)}{x - a}\).Application à la fonction exponentielle
Prenons par exemple la fonction exponentielle. On a \(\frac{e^x - e^0}{x - 0}\). Cela semble un peu compliqué, mais comment allons-nous modifier cela pour le faire apparaître comme la définition du nombre dérivé ? Nous identifions que notre \(a\) ici est zéro, notre \(f(x)\) est \(e^x\) et notre \(f(a)\) devrait être \(e^0\). Sauf que \(e^0\) est égal à 1. Donc, nous avons bien la limite quand \(x\) tend vers zéro de \(\frac{e^x - e^0}{x - 0}\), soit la limite quand \(x\) tend vers zéro de \(\frac{e^x - 1}{x}\). Cela correspond au nombre dérivé de la fonction exponentielle calculé en 0. Sauf que la dérivée de la fonction exponentielle en 0 est \(e^0\), soit 1. Donc, la limite est égale à 1. C'est une petite astuce à retenir, elle peut être le point bonus d'un contrôle. J'aimerais que vous vous en souveniez. À vous de jouer, nous vous avons préparé des exercices en dessous.Nouvelle recrue
Invité
0 pts
