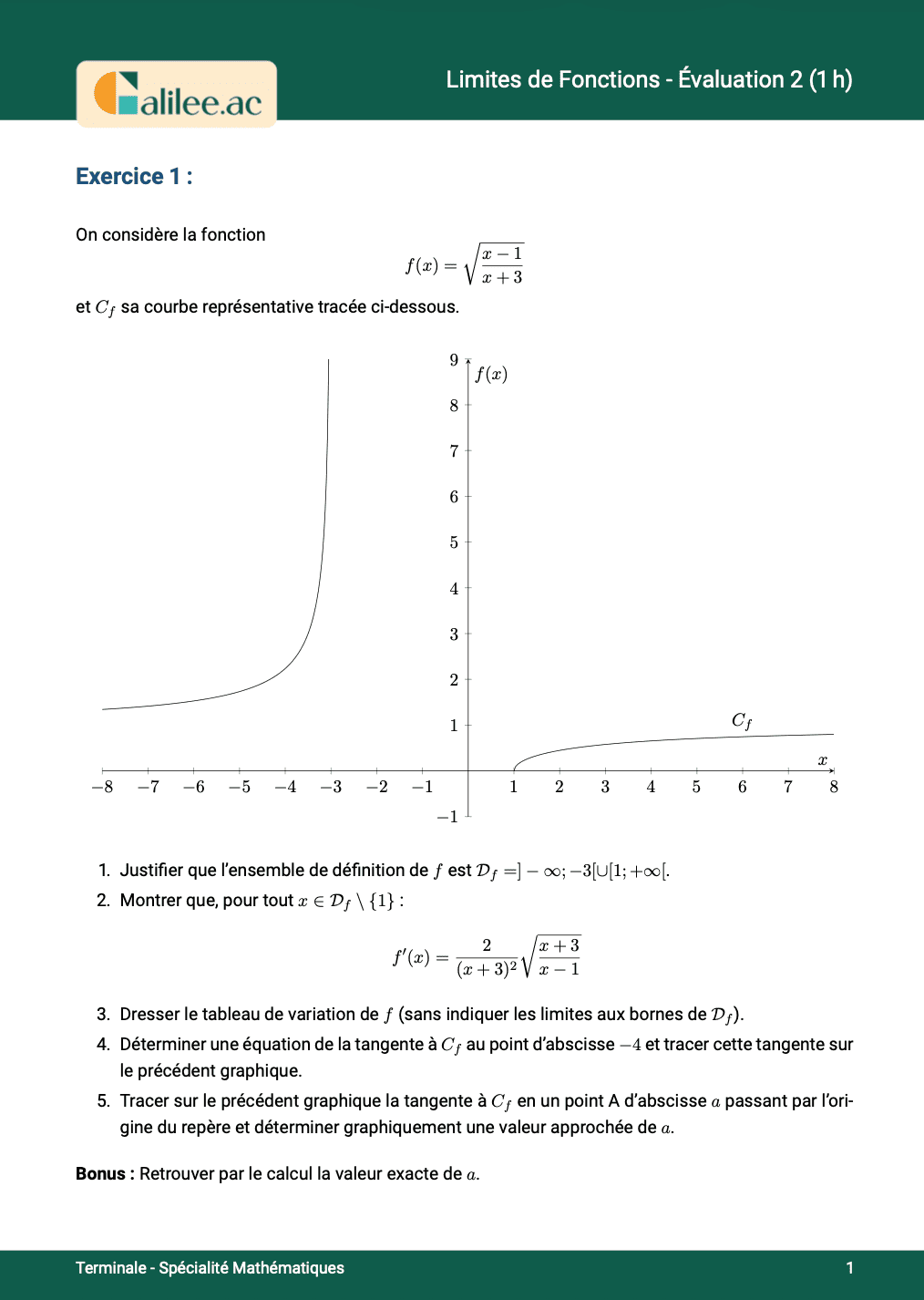
Livre
1. Les limites de base
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour essayer de comprendre rapidement le principe de limite avec des fonctions. On se fait ça tout de suite. Une limite, c'est une expérience de pensée. Une limite, c'est de dire à quoi ressemblerait ma fonction, par exemple \(x - 3\), dans une hypothèse absurde, qui est par exemple que \(X\) soit infiniment grand.Exemples de limites
Si je prends la fonction \(2x\) (deux fois la variable \(X\)) et que je m'amuse à imaginer que la variable \(x\) devient infiniment grande, la variable \(2x\), est-ce qu'elle va être infiniment grande ? Est-ce qu'elle va être infiniment petite ? Est-ce qu'elle va valoir \(\pi\) ? Est-ce qu'elle va valoir \(-2\) ? C'est ça la question qu'on vous pose. Si \(X\) devient infiniment grand, \(2x\) a priori ça devient deux fois plus infiniment grand. Sauf que l'infini a ça de magique que infini fois 2 égal l'infini. Donc la limite de \(2x\) quand \(x\) tend vers l'infini, c'est l'infini. Vous commencez à le savoir, a priori vous l'avez déjà vu avec les suites. On commence : la limite d'une fonction \(f\) de \(x = 1\) quand \(x\) tend vers l'infini. Là, c'est les cas simples. Pourquoi ? Parce que la fonction \(x = 1\) elle est constante. Donc si je m'amuse à représenter cette fonction, donc je mets un axe horizontal, un axe vertical, ma fonction \(f(x)=1\) c'est une fonction constante qui est horizontale. Quand je fais la limite en plus l'infini, c'est je me pose sur cette courbe et je vais voir ce qui se passe infiniment loin à droite. Infinitement loin à droite, mon image, mon \(f(x)\), il vaut toujours 1. La limite de \(f(x)\) quand il tend vers l'infini, c'est un.Autres exemples de limites
Autrement dit, quand il n'y a pas de \(X\) dans l'expression de la fonction, la limite ne change pas la valeur de la fonction. La limite de \(X - 3\) quand \(x\) tend vers 3, attention, une limite ce n'est pas forcément quelque chose qu'on va calculer en plus ou moins l'infini. On peut aussi la calculer en 0, c'est-à-dire s'imaginer ce que vaudrait la fonction si \(X\) se rapprochait infiniment près de 0. Mais on peut aussi la calculer en 3, s'imaginer ce que devient \(x -3\) quand \(x\) devient infiniment proche de 3. Si je prends un nombre qui est infiniment proche de 3 et que je lui enlève 3, qu'est-ce que je me retrouve ? Je me retrouve avec un truc qui est infiniment proche de zéro. On continue : la limite quand \(x\) tend vers l'infini de \(2x\), là c'est le cas le plus simple. Si \(x\) tend vers l'infini, \(X\) il tend vers quoi ? Histoire aussi, si on est vers plus l'infini, si on est vers moins l'infini, qu'est-ce qui se passe si \(x\) tend vers moins l'infini et qu'on cherche à savoir vers quoi tend \(X^2\) ? Si \(x\) tend vers moins l'infini, \(X^2\) il tend vers moins l'infini fois moins l'infini, donc un truc infiniment grand. La limite de \(X^3\) quand \(x\) tend vers moins l'infini, donc cette fois-ci on se doute bien que bon, il tend vers moins l'infini, ça va encore être un truc infiniment grand parce que l'infini fois l'infini, ça fait l'infini, ça fait un truc extrêmement grand. La question, c'est le signe. J'ai un moins là, j'ai un cube, donc on va faire moins fois moins fois moins. Autrement dit, quand le nombre qui est là est impair, je finis avec un truc positif. Quand le nombre qui est là est pair, si je pars vers moins l'infini, j'arrive à quelque chose infiniment grand mais négatif. Et enfin, la fonction racine : en plus l'infini, \(\sqrt{x}\) ça fait plus l'infini et en 0, \(\sqrt{x}\) ça fait 0. Mais ça, on le verra plus tard. On vous a mis des petits exercices pour commencer, entraînez-vous, vous allez voir, c'est très très simple. À vous de jouer !Recrue
Visiteur anonyme
13 pts