Livre
10. Démontrer que deux vecteurs sont orthogonaux
Conditions d'achèvement
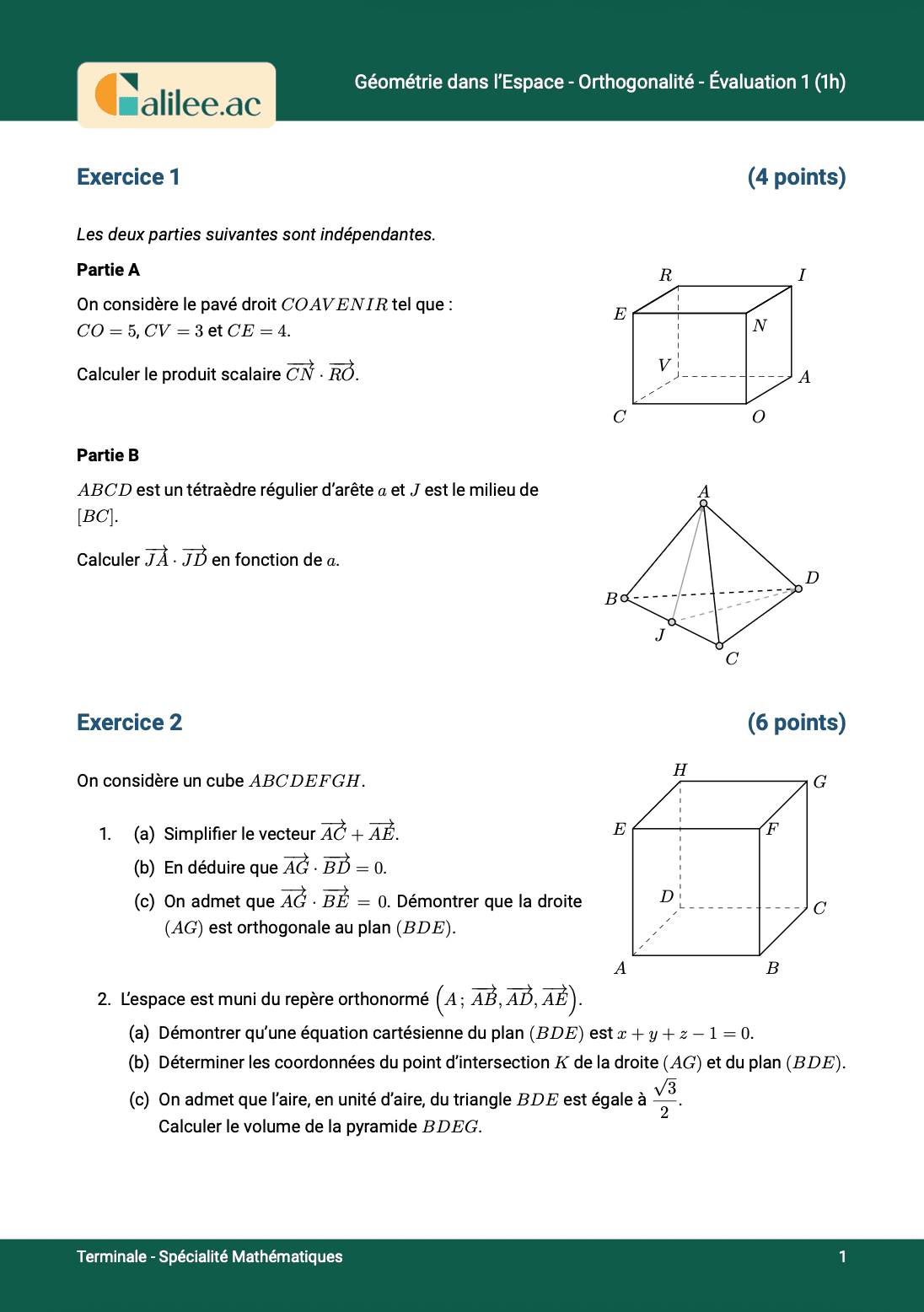
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Exercice
5
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, nous allons voir très calmement comment démontrer que deux vecteurs sont orthogonaux. On se fait ça tout de suite.Démonstration de l'orthogonalité de deux vecteurs
Dans l'espace, quand vous avez les coordonnées pour démontrer que deux vecteurs sont orthogonaux, vous avez un réflexe : le produit scalaire. Lorsque des vecteurs sont orthogonaux, le produit scalaire est égal à zéro. Dans ce cas-là, je calcule le produit scalaire : \(1 \times -1 + 2 \times -2 + 3 \times 0\). Cela donne \(-1 - 4 + 0\), qui est égal à \(-5\). Est-ce que \(-5\) est égal à zéro ? Non, donc ces vecteurs ne sont pas orthogonaux.Exercices et entraînement
C'était juste pour vous présenter les exercices qui sont en dessous. On l'a fait avec un exemple donné, mais dans la réalité, vous allez calculer les produits scalaires de plein de manières différentes. En tout cas, entraînez-vous, parce que ça sert pour ce chapitre et pour le chapitre suivant. À vous de jouer, vous êtes des champions !Nouvelle recrue
Visiteur anonyme
0 pts