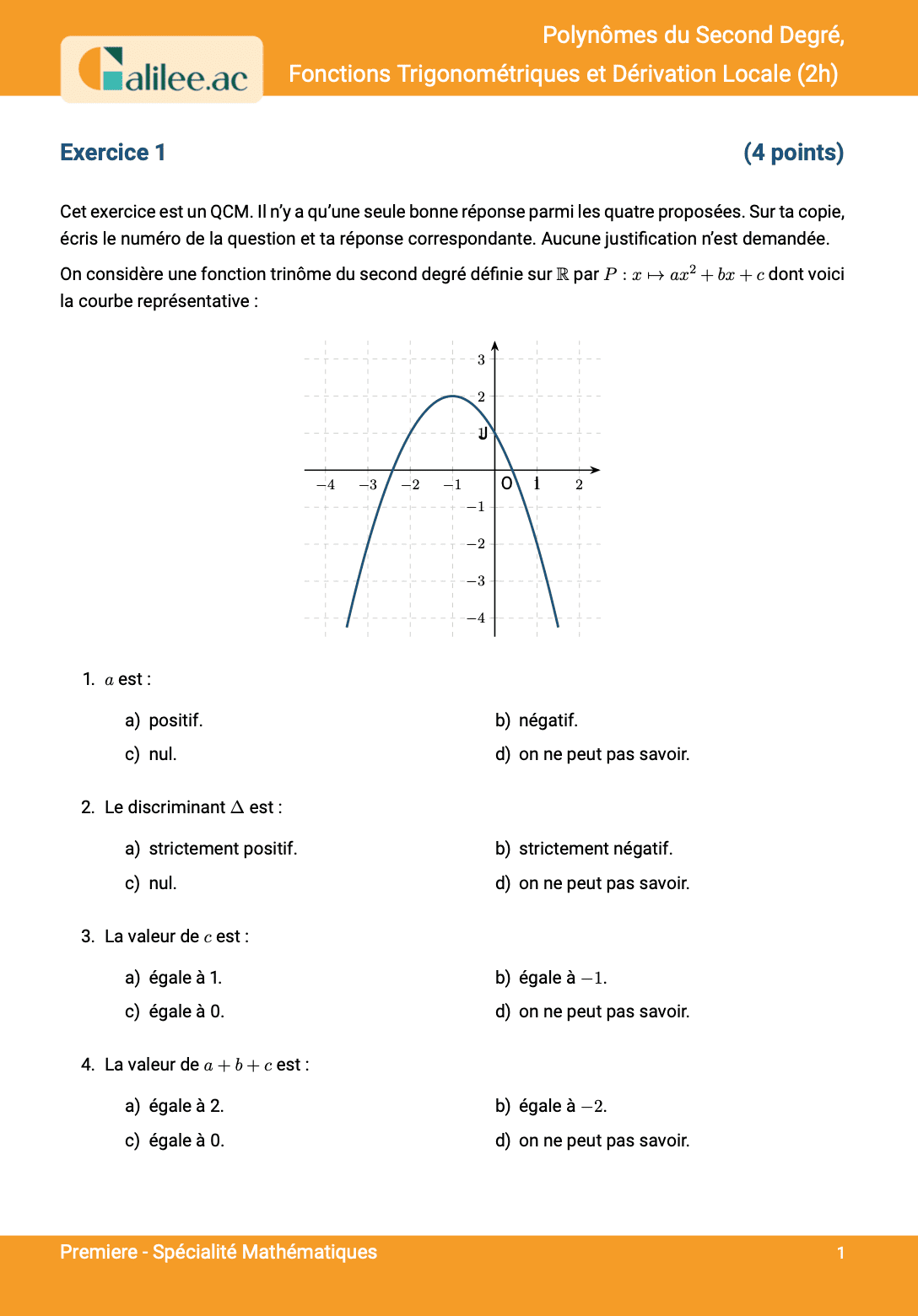
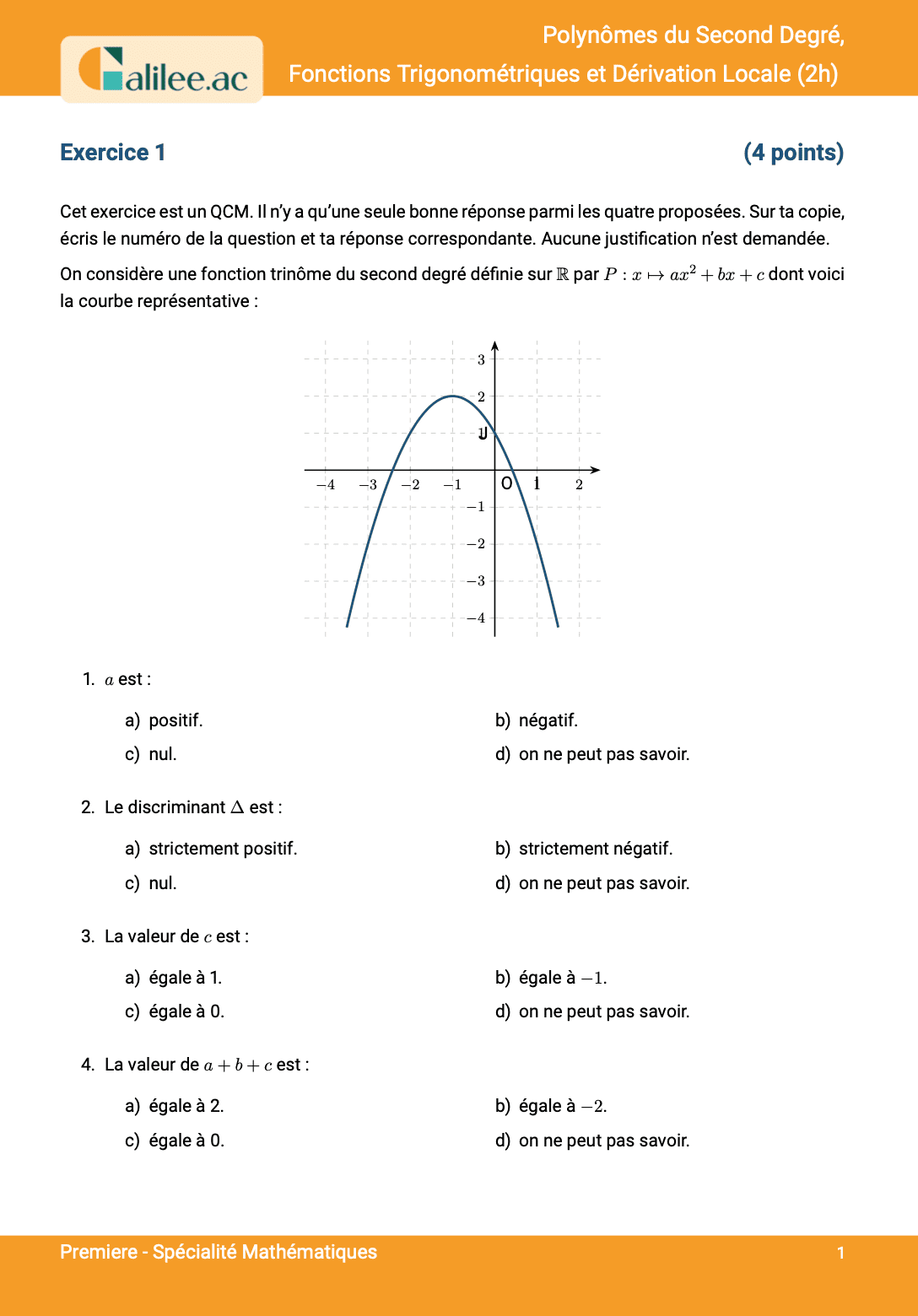
23. Résoudre une équation de degré 3 grâce au 2nd degré

Introduction

Allons-y, les amis, nous allons résoudre une équation de degré 3 en utilisant la factorisation. C'est un exercice qui vaut trois points sur le contrôle. Nous avons un polynôme \(x^3 - 6x^2 + 10x - 3 = 0\). Le problème est que ce polynôme n'est pas de degré 2 comme vous avez l'habitude de le faire, mais il est de degré 3. Donc, si vous essayez de calculer le delta, vous allez échouer parce qu'il y aura un \(x^3\) et non un \(x^2\). Comment allons-nous faire ? Eh bien, nous allons diviser l'exercice en deux parties.

Première partie : Factorisation du polynôme

La première partie consiste à écrire ce polynôme de degré 3, qui vaut zéro, comme un produit d'un polynôme de degré 2 et d'un polynôme de degré 1. Une fois que j'ai réussi à le faire, pour savoir quand est-ce que ce produit vaut zéro, je me rends compte que j'ai \(a \times b = 0\). Donc, soit \(a = 0\), soit \(b = 0\). Si \(a = 0\), nous avons une solution facile \(x = 3\). Si \(b = 0\), nous avons un polynôme du second degré classique que vous savez résoudre en calculant le delta et les racines. Donc, nous prenons un polynôme de degré 3, nous le divisons en deux polynômes de degrés plus petits qui seront plus simples à résoudre pour trouver quand est-ce qu'il vaut 0. Nous cherchons à trouver \(a\), \(b\) et \(c\) tels que notre polynôme, soit égal à \((x - 3)(ax^2 + bx + c)\).

Deuxième partie : Résolution du système d'équations

Pour cela, nous allons développer \((x - 3)(ax^2 + bx + c)\) et trier les termes en fonction de la puissance de \(x\). Ensuite, nous allons établir un système d'équations en égalant les coefficients des termes de même degré de notre polynôme développé et de notre polynôme initial. Nous résolvons ce système pour obtenir les valeurs de \(a\), \(b\) et \(c\). Une fois que nous avons trouvé \(a\), \(b\) et \(c\), nous pouvons écrire notre polynôme initial sous la forme \((x - 3)(ax^2 + bx + c) = 0\).

Troisième partie : Résolution de l'équation

Maintenant, pour résoudre l'équation initiale, nous allons utiliser la forme factorisée de notre polynôme. Pour résoudre \(x^3 - 6x^2 + 10x - 3 = 0\), cela revient à résoudre \((x - 3)(ax^2 + bx + c) = 0\). Cela signifie soit \(x - 3 = 0\), soit \(ax^2 + bx + c = 0\). La première équation est facile à résoudre et donne \(x = 3\). Pour la deuxième équation, nous calculons le discriminant et trouvons les racines. Ainsi, nous obtenons trois solutions pour notre équation de degré 3. En résumé, pour résoudre un polynôme de degré 3 égal à zéro, nous ne pouvons pas le faire directement. Nous devons donc le transformer en un produit d'un polynôme de degré 2 et d'un polynôme de degré 1, résoudre un système d'équations pour trouver les coefficients de ces polynômes, puis résoudre les équations obtenues. C'est un exercice intéressant et important à maîtriser. Alors, à vous de jouer !