Livre
9. Trouver un angle grâce à 2 produits scalaires différents
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
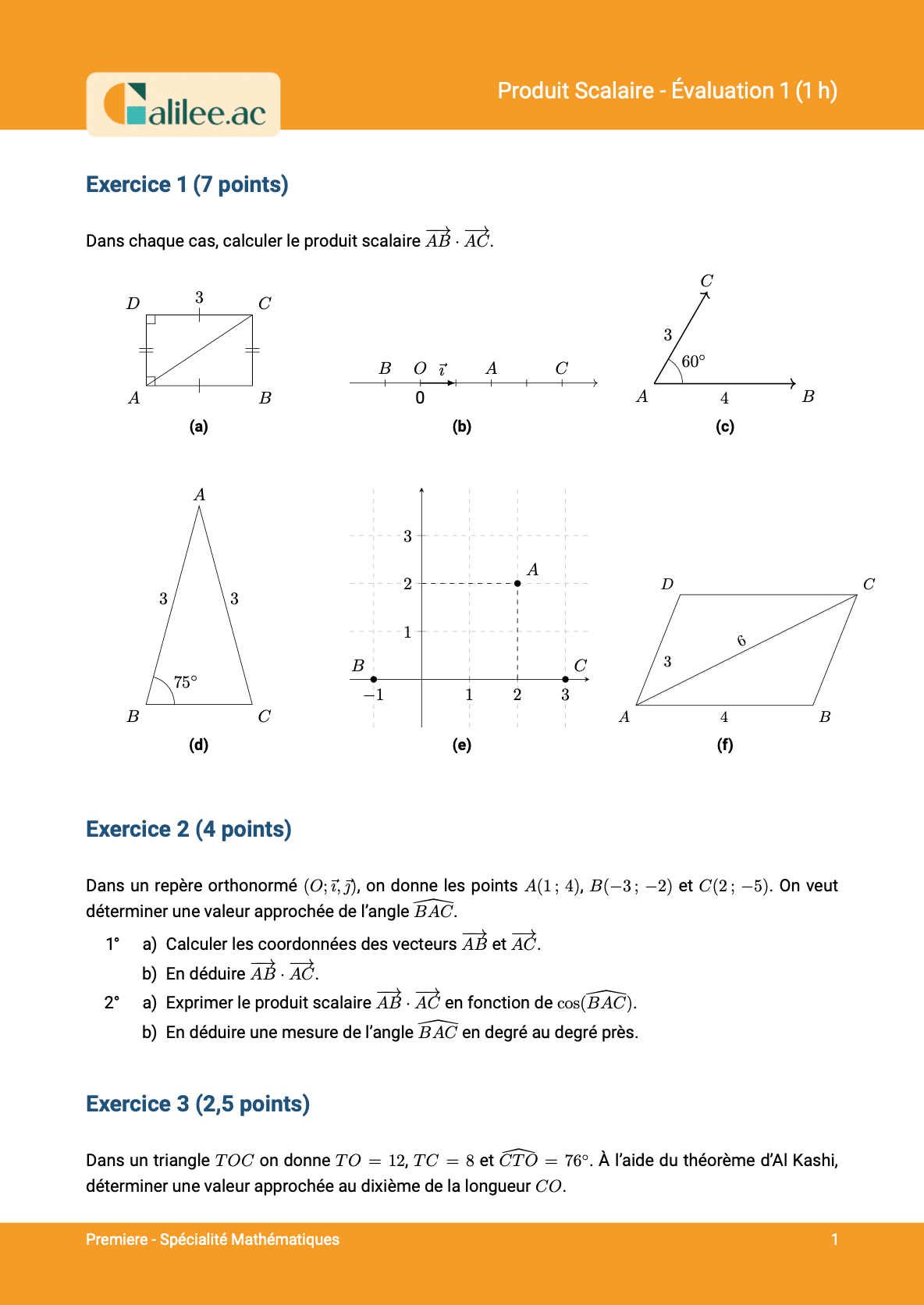
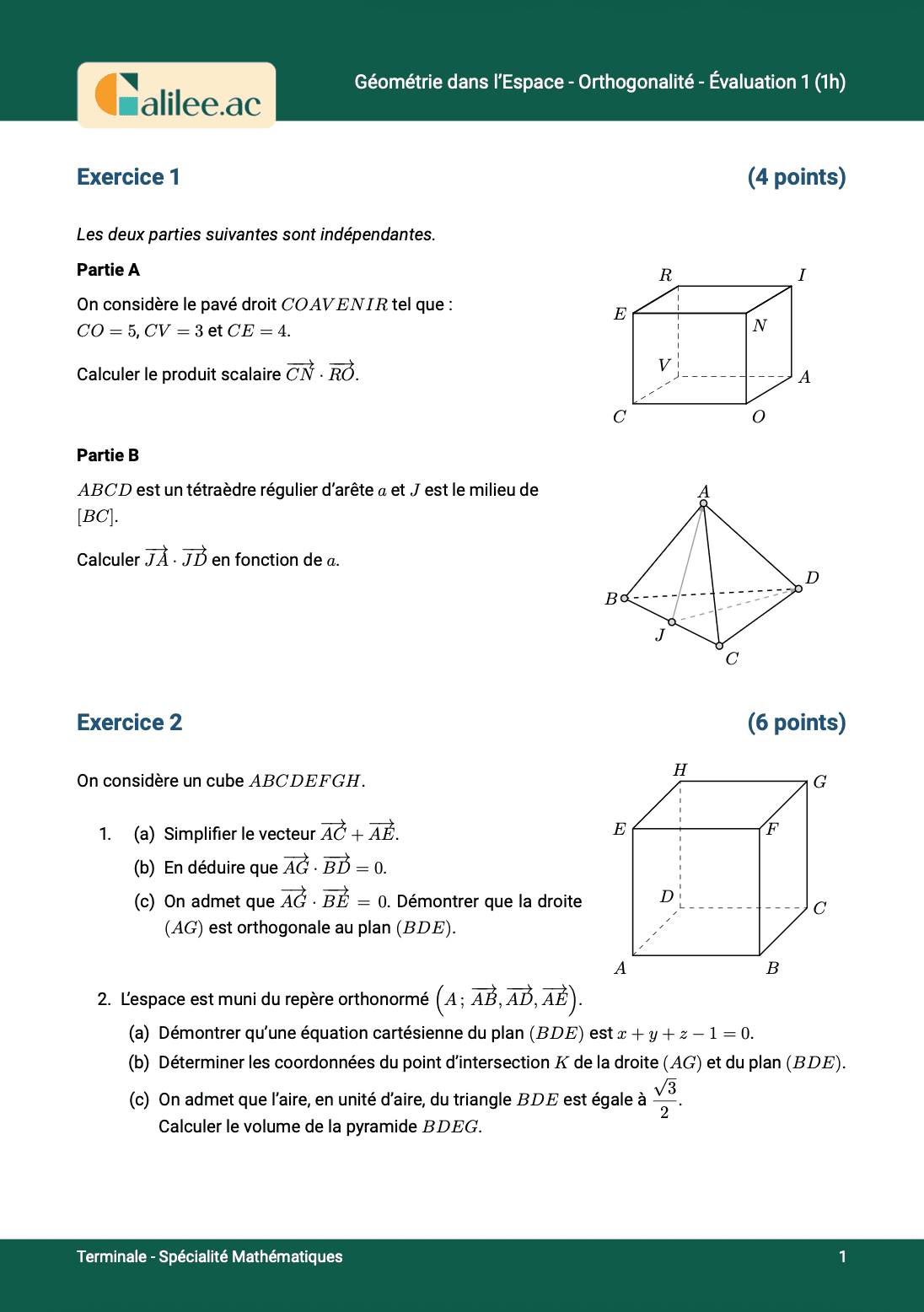
Allez les amis, on est parti sur un exercice typique de ce que vous avez au contrôle. C'est-à-dire utiliser deux manières différentes de calculer le produit scalaire pour trouver l'angle entre deux vecteurs. On vous donne un triangle quelconque \(ABC\) avec les coordonnées de tous les points et on vous demande de calculer \(\overrightarrow{AB} \cdot \overrightarrow{AC}\) pour trouver l'angle \(ABC\).Première méthode de calcul
La première méthode que je vous propose est de calculer l'angle, que nous allons appeler \(\alpha\), en utilisant la formule du produit scalaire : \(\overrightarrow{AB} \cdot \overrightarrow{AC} = ||\overrightarrow{AB}|| \times ||\overrightarrow{AC}|| \times \cos(\alpha)\). Pour calculer les coordonnées du vecteur \(\overrightarrow{AB}\), on fait \(x_B - x_A\) et \(y_B - y_A\). Donc \(x_B = 0\) et \(x_A = 0\), donc \(0 - 0 = 0\). Pour \(y_B\) et \(y_A\), on a \(4 - 0 = 4\). Pour le vecteur \(\overrightarrow{AC}\), ses coordonnées sont \(3 - 0 = 3\) et \(3 - 0 = 3\). Maintenant, je peux calculer la norme de \(\overrightarrow{AB}\) avec la formule de la norme : \(||\overrightarrow{AB}|| = \sqrt{0^2 + 4^2} = 4\). La norme de \(\overrightarrow{AC}\) est \(||\overrightarrow{AC}|| = \sqrt{3^2 + 3^2} = \sqrt{18}\). En remplaçant dans la formule du produit scalaire, on obtient : \(4 \times \sqrt{18} \times \cos(\alpha)\).Deuxième méthode de calcul
La deuxième méthode consiste à utiliser le produit scalaire avec les coordonnées. On peut dire que \(\overrightarrow{AB} \cdot \overrightarrow{AC} = x \times x' + y \times y'\). Donc \(0 \times 3 + 4 \times 3 = 12\). Maintenant, on peut égaler les deux expressions du produit scalaire : \(4 \times \sqrt{18} \times \cos(\alpha) = 12\). En isolant \(\cos(\alpha)\), on obtient \(\cos(\alpha) = \frac{12}{4 \times \sqrt{18}} = \frac{3}{\sqrt{18}}\). En utilisant la calculatrice pour faire l'opération inverse du cosinus, on trouve que \(\alpha = \cos^{-1}\left(\frac{3}{\sqrt{18}}\right) \approx 45\) degrés.Conclusion
Donc, quand vous devez trouver l'angle en utilisant deux méthodes de calcul du produit scalaire, il y en a une que vous aurez toujours à faire, celle qui vous permet de faire apparaître \(\alpha\). Ensuite, vous pouvez utiliser au choix soit les coordonnées, soit le produit scalaire. Ce qui est important, c'est que vous arriviez à calculer la valeur du produit scalaire. Une fois que vous l'avez calculé de deux manières différentes, vous dites que la première manière est égale à la deuxième, donc ça égale ça. Vous faites un coup de calculatrice et vous avez l'angle. À vous de jouer !Nouvelle recrue
Visiteur anonyme
1 pts