7. Chasles avec les produits scalaires

Introduction

Allez les amis, on va voir aujourd'hui peut-être la plus importante des compétences, celle qui consiste à utiliser Chasles pour calculer des produits scalaires. Elle marche dès que vous avez un angle droit. On y va.

La relation de Chasles

La relation de Chasles est une relation qui vous dit finalement que quand je vais d'un point B à un point C en tant que vecteur, je peux tout à fait dire que plutôt que d'aller de B à C, je vais d'abord de B à A, ensuite de A à C. C'est ce qui s'affiche lors du cours. Ce que j'aimerais que vous mettiez en tête, c'est que dès que vous avez un angle droit, vous allez exprimer tous les vecteurs qui sont en jeu de manière à ne passer que par des côtés qui sont à angle droit. Par exemple, si vous voulez calculer \(BC\), \(BA\) est bien, il est sur un des côtés qui a un angle droit. Par contre \(AC\), il est sur une diagonale qui n'a pas d'angle droit. Vous avez bien sûr l'option d'utiliser la formule des longueurs, mais on ne va pas le faire comme ça. Moi, je veux dire que \(BC\) est plutôt \(BA + AC\), et c'est ça que je vais écrire dans la formule.

Application de la formule

Donc ma formule devient \(BA + AC\). C'est là qu'intervient la deuxième formule. Une fois que vous avez écrit ça, il va falloir développer votre produit. Autrement dit, transformer un produit qui a l'air compliqué en deux produits scalaires qui sont simples. Regardez ce qui se passe si vous aviez \(x + y\) multiplié par \(x^3\) avec des parenthèses et que vous vouliez le développer. Vous diriez que ça fait \(x \cdot x^3 + y \cdot x^3\). Jusque là, ça ne poserait aucun problème. Mais avec les vecteurs, c'est exactement la même chose. Quand vous avez \(BA + AC\) en produit scalaire, ça fait \(BA \cdot BA + AC \cdot BA\). J'ai juste distribué comme vous l'auriez fait avec des nombres. Maintenant, regardez pourquoi c'est joli. Parce que \(AC\) est perpendiculaire à \(BA\), et vous savez que quand il y a un angle droit entre deux vecteurs, autrement dit que ces vecteurs sont orthogonaux, le produit scalaire est nul. Donc il vous reste juste \(BA \cdot BA\), tout simplement. À partir de là, vous pouvez dire que c'est la norme de \(BA\) fois la norme de \(BA\) fois le cosinus de l'angle entre \(BA\) et \(BA\). Mais c'est quoi le cosinus de l'angle entre \(BA\) et \(BA\)? Vu que ces deux vecteurs sont les mêmes, de combien je dois tourner pour passer de l'un à l'autre? L'angle est de 0, donc le cosinus de 0 est 1. La norme de \(BA\) est 7, donc je me retrouve avec \(7 \times 7 = 49\). Est-ce que vous voyez la puissance du truc? On a transformé un produit qui a l'air compliqué en deux produits scalaires extrêmement simples grâce à Chasles et grâce à la distribution.

Exercice pratique

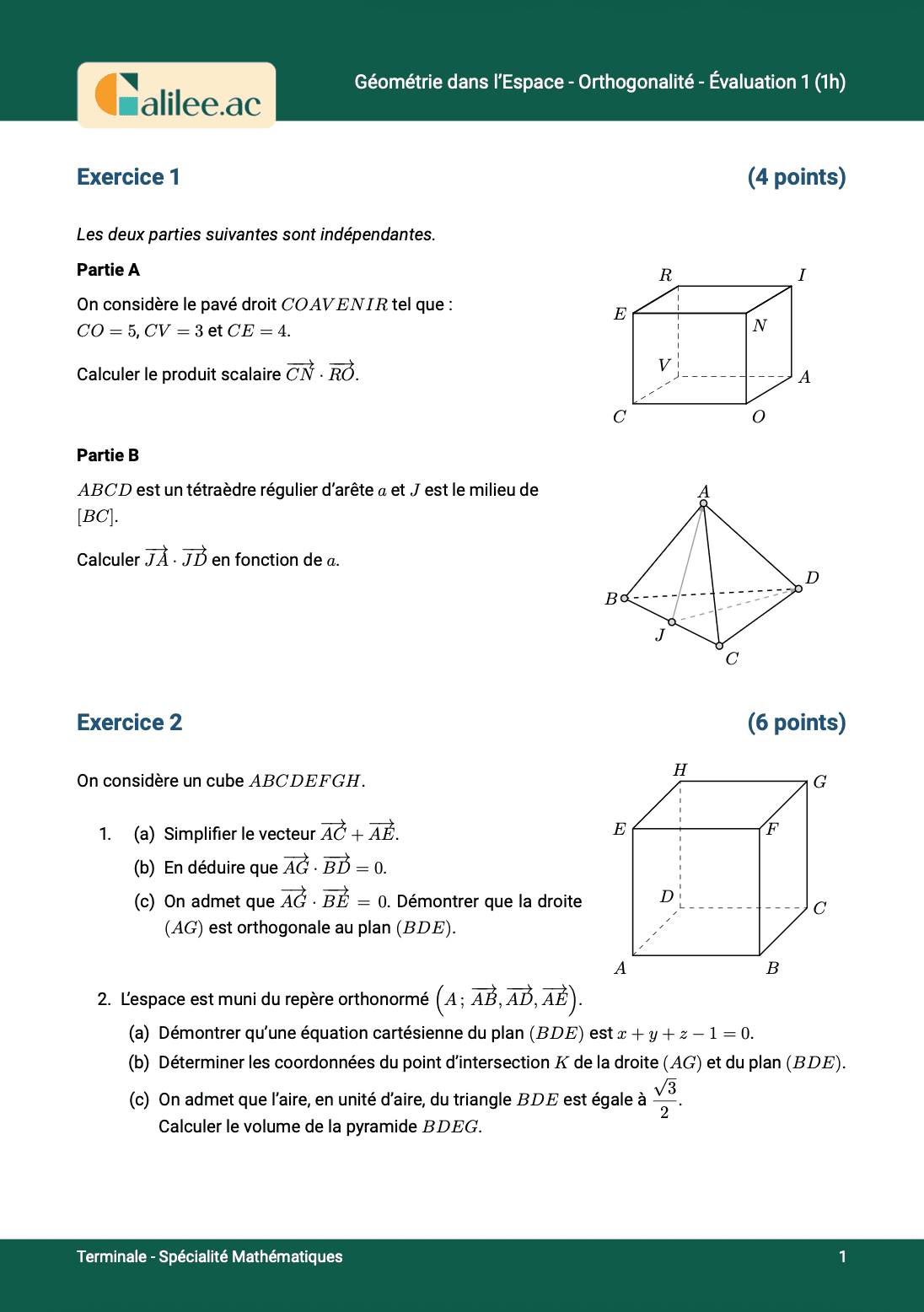
Prenons un exemple. On vous donne un rectangle, on vous donne deux côtés du rectangle et on vous dit que le point E est au milieu de \(BC\) et de \(DE\), puisqu'on a la même longueur ici et ici. Donc moi, je vais commencer par compléter les longueurs. Si j'ai 6 ici, là j'ai la moitié donc j'ai 3, et là j'ai la moitié aussi donc j'ai 3. On vous demande le produit scalaire \(AD \cdot BD\). Dans ce type de situation, la seule option c'est Chasles. Vous avez des angles droits sur tous les côtés, donc vous devez prendre vos deux vecteurs et les exprimer de manière à ce qu'ils ne passent que par les côtés où il y a des angles droits. Je commence avec \(AD\). Comment est-ce que je peux partir de \(A\) et arriver jusqu'à \(D\) en passant que par des angles droits? C'est pas compliqué, je passe par \(B\) et \(E\). Donc \(AD = AB + BE + ED\). Maintenant, j'ai que des côtés qui sont le long d'un angle droit. De la même manière que quand j'avais \(BA + AC\) en produit scalaire, je faisais une distribution, là je vais faire une double distribution. Donc je vais faire \(AB \cdot AB + AB \cdot BE + AB \cdot ED + BE \cdot AB + BE \cdot BE + BE \cdot ED\). On a transformé un produit scalaire compliqué en six produits scalaires, mais ces six produits scalaires vont être beaucoup plus simples que ce qu'on avait initialement. Maintenant, je peux utiliser la formule et les normes parce que \(AB\) et \(BE\) ont une longueur connue. \(AB\) vaut 3 donc ça me fait \(3 \times 3\). Pour l'angle entre \(AB\) et \(BE\), si l'angle entre les deux ne vous semble pas évident, recopiez les vecteurs cul à cul. Pour passer de \(AB\) à \(BE\), il faut tourner de 180 degrés, autrement dit en radians, ça fait \(\pi\). Pour \(BE \cdot ED\), les vecteurs ont le même sens donc l'angle entre eux est de 0. J'ai pas besoin de tourner. La norme de \(AB\) vaut 3, la norme de \(BE\) vaut 3, et le cosinus de \(\pi\) fait -1. Donc ça me fait \(-9\). La norme de \(BE\) vaut 3, la norme de \(ED\) vaut 6, et le cosinus de 0 fait 1. Donc ça me fait \(18\). Donc le produit scalaire \(AD \cdot BD\) est égal à \(-9 + 18 = 9\). C'est un peu chaud et ça prend du courage parce que vous transformez votre petit produit scalaire en six produits scalaires. Mais regardez, on a deux qui sont nuls et les quatre qui restent sont ultra simples parce que vous connaissez les angles. C'est soit ils sont dans le même sens, soit ils sont opposés. L'avantage de Chasles, c'est que vous vous retrouvez plus qu'avec deux possibilités pour l'angle : soit ils sont perpendiculaires, soit ils sont parallèles. C'est terminé, entraînez-vous. Ça, ça tombe au contrôle, littéralement exactement cet exercice on vous en donnera.