Livre
6. Vérifier que 2 vecteurs sont orthogonaux
Conditions d'achèvement
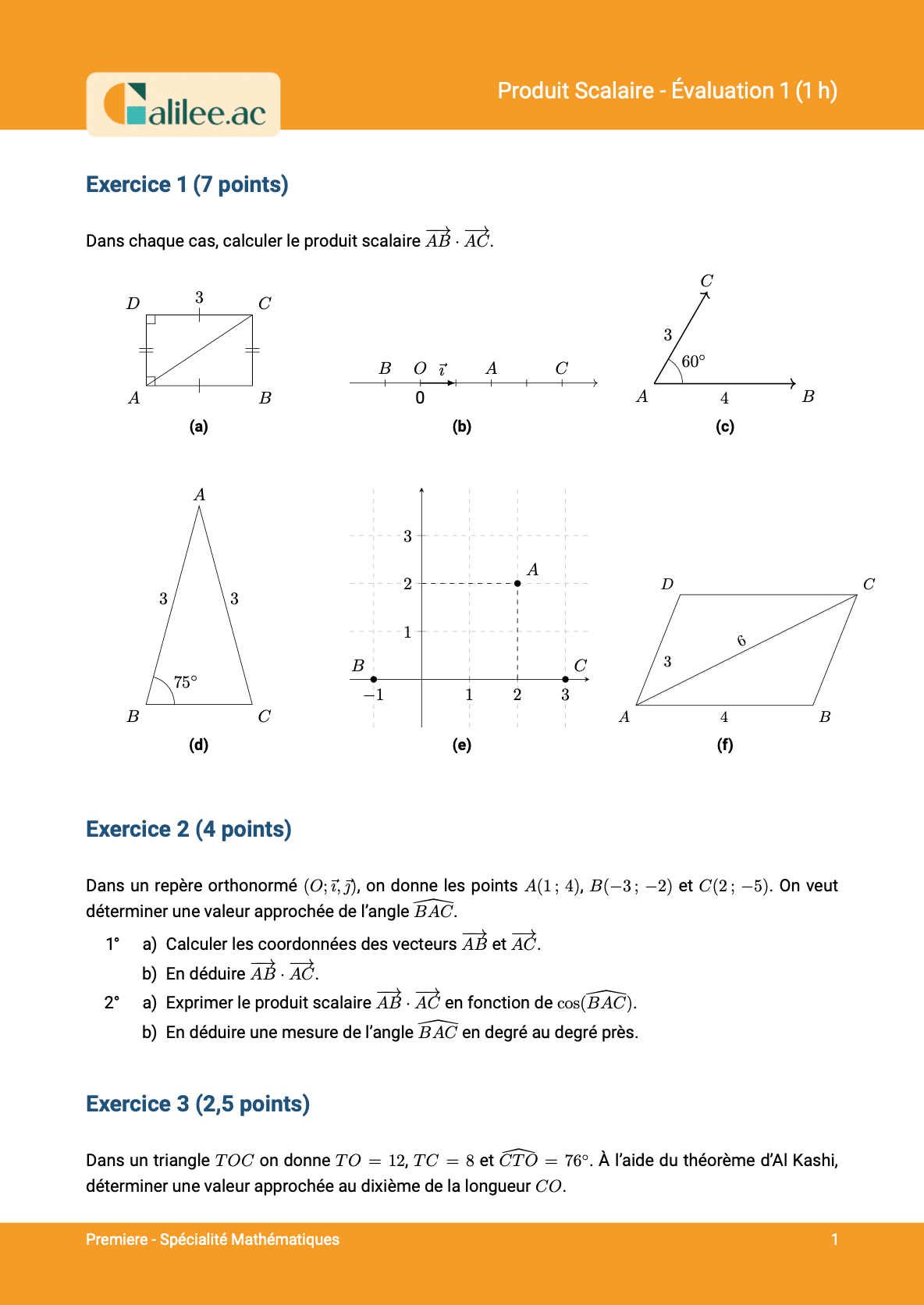
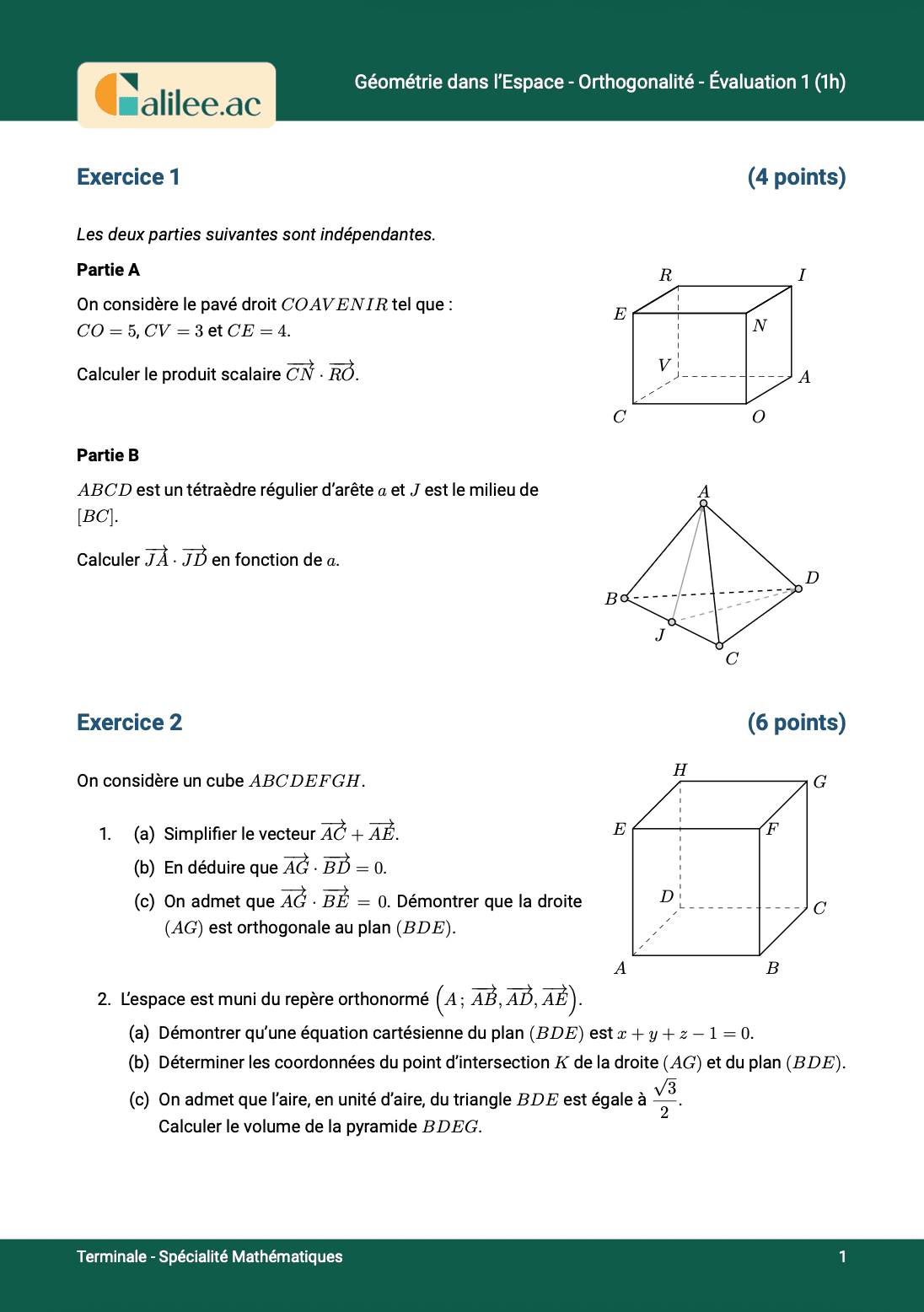
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez, les amis, on est parti pour voir comment utiliser le produit scalaire pour montrer que des vecteurs sont orthogonaux. On y va ! Je vous affiche ce que vous devez marquer sur votre fiche. À gauche, deux vecteurs sont orthogonaux quand leur produit scalaire vaut zéro. C'est aussi simple que ça et ça marche dans l'autre sens : si le produit scalaire de deux vecteurs vaut zéro, alors ces vecteurs sont orthogonaux.Exemple 1
Vrai ou faux ? Est-ce que ces deux vecteurs sont orthogonaux ? Moi, je ne vais pas m'embêter, je vais calculer le produit scalaire des deux vecteurs. Donc, je vais utiliser la technique de calcul avec les coordonnées. C'est \(1 \times 2 + (-2) \times (-2) + (-3) \times 3\). \(2 - 4 - 9 = -11\), ce qui est différent de 0, donc c'est faux. C'est aussi simple que ça.Exemple 2
On va commencer ici jusqu'à arriver à \( \sqrt{2} \times \sqrt{2} + (-1) \times 1\). Cela fait \(2 - 1 = 1\), ce qui est différent de 0, donc ils ne sont pas orthogonaux. C'est aussi bête que ça. À vous de jouer maintenant ! On vous attend dans la suite. [Musique]Recrue
Visiteur anonyme
7 pts