Introduction
Allons-y, les amis, nous allons calculer des produits scalaires dans des parallélogrammes en utilisant la formule des normes. Vous savez maintenant comment calculer des produits scalaires dans un triangle quelconque. Regardons ce qu'est un parallélogramme. N'est-ce pas simplement un premier triangle quelconque et un deuxième triangle quelconque ? C'est exactement ce dont nous allons nous servir pour calculer les produits scalaires demandés.
Calcul des produits scalaires
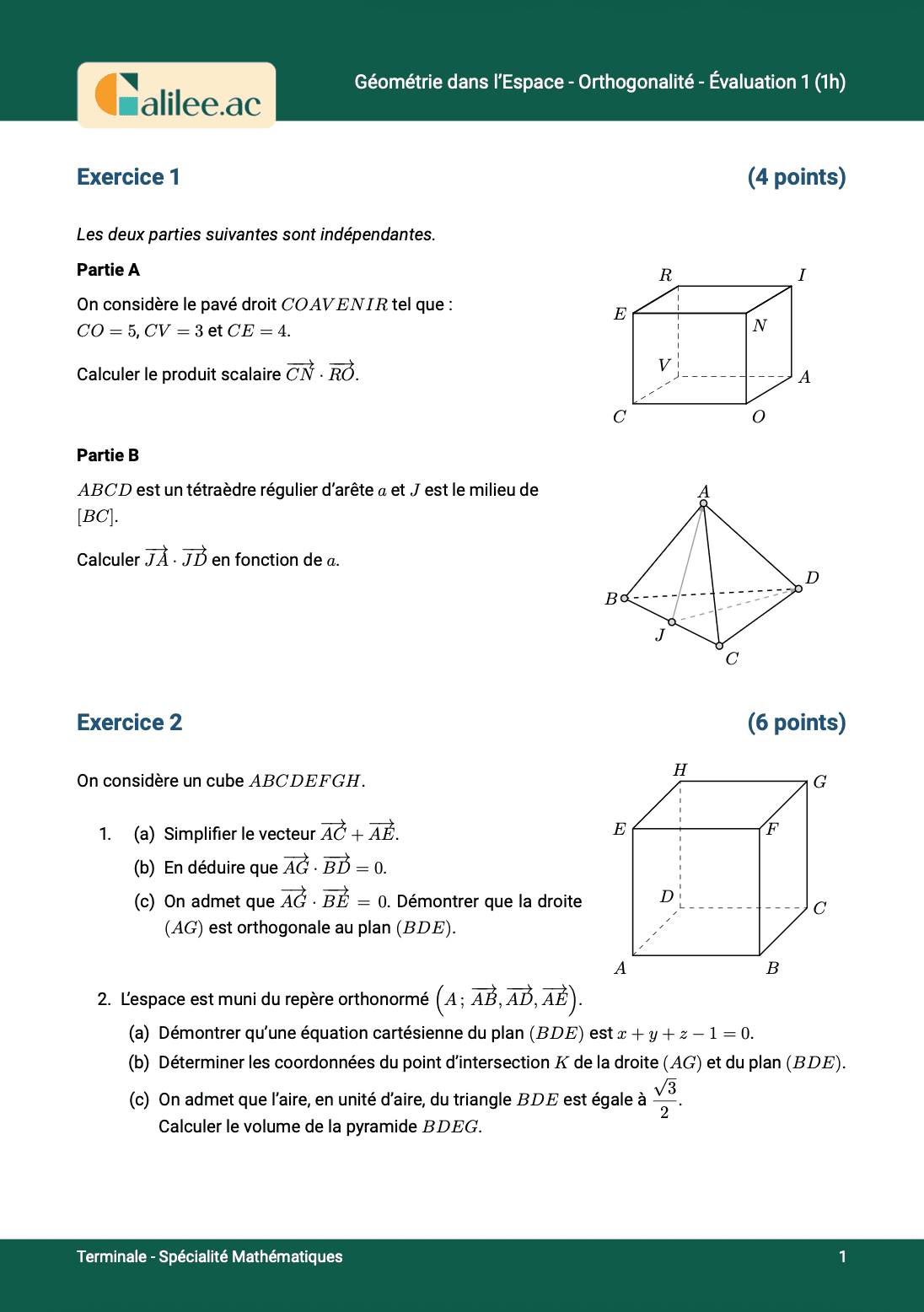
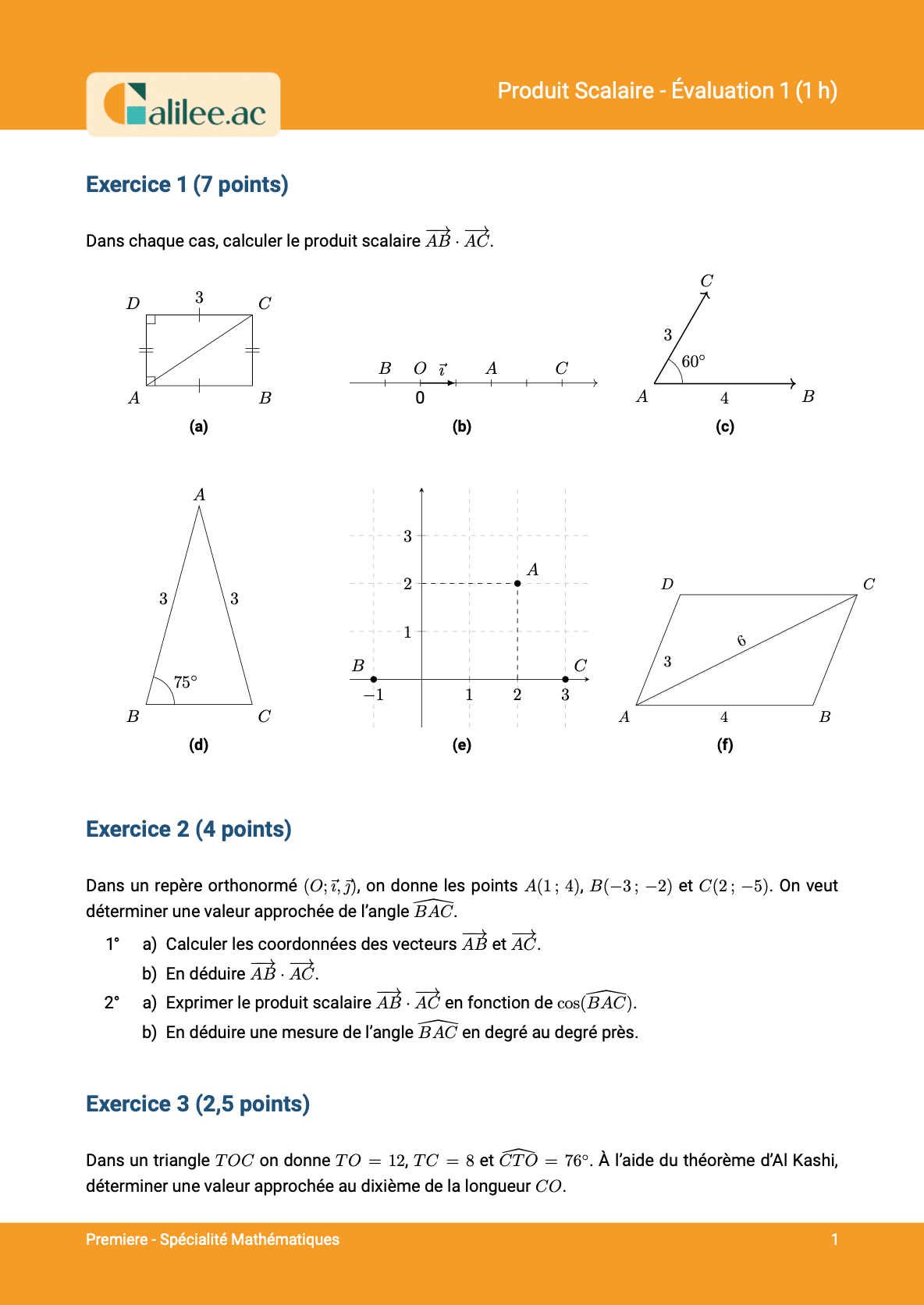
Nous commençons par reporter les longueurs. Je vous rappelle qu'un parallélogramme a des côtés opposés de longueurs égales. Donc, si \(AB = 8\), alors \(DC = 8\), et si \(BC = 3\), alors \(AD = 3\).
Nous attaquons alors le premier produit scalaire, \(AB \cdot BC\). Nous devons d'abord déterminer dans quel triangle nous nous trouvons, à savoir \(ABC\). Je vais recopier mes deux formules de normes. Vous vous souvenez qu'à chaque fois, nous avons deux possibilités :
1. \(AB \cdot BC = \frac{1}{2} (||AB||^2 + ||BC||^2 - ||AC||^2)\)
2. \(AB \cdot BC = \frac{1}{2} (||AB||^2 + ||AC||^2 - ||BC||^2)\)
Je vous rappelle que vous devez écrire les deux formules au début, car vous ne savez pas laquelle des deux sera la plus intéressante à utiliser.
Choix de la formule
Maintenant, nous allons déterminer quelle formule est la plus intéressante à utiliser. Pour ce faire, nous allons marquer les longueurs que nous connaissons. Nous connaissons déjà \(AB = 3\) et \(BC = 8\). Maintenant, nous allons nous demander si \(AB - BC\) ou \(AB + BC\) est plus facile à calculer. Pour moi, \(AB + BC\) est plus facile à calculer, car cela donne simplement \(11\). Donc, je connais aussi cette longueur. Par conséquent, je n'ai pas besoin d'utiliser la première formule, car la deuxième fonctionne. Je calcule donc :
\[\frac{1}{2} (11^2 - 3^2 - 8^2) = \frac{1}{2} (121 - 9 - 64) = \frac{1}{2} (48) = 24\]
Technique rapide pour choisir la formule
Maintenant, essayons une technique un peu plus rapide pour déterminer quelle formule utiliser. Vous remarquerez que dans les deux cas, nous avons \(AB + BC\). Donc, dans les deux cas, nous allons trouver ces longueurs. La question que nous allons nous poser est : avons-nous plutôt intérêt à calculer \(AB - BC\) ou \(AB + BC\) ?
Si les deux vecteurs que vous voulez calculer sont consécutifs, alors vous utiliserez la formule avec \(u + v\). Si les deux vecteurs ne sont pas consécutifs, alors vous utiliserez la formule avec \(u - v\).
Conclusion
Vous voyez à quel point cet outil est puissant. En vous demandant simplement si vous allez utiliser la formule avec \(u + v\) ou celle avec \(u - v\), vous savez directement quelle formule utiliser. À vous de jouer maintenant !