4. Calculer un produit scalaire avec les normes dans un triangle quelconque

Introduction

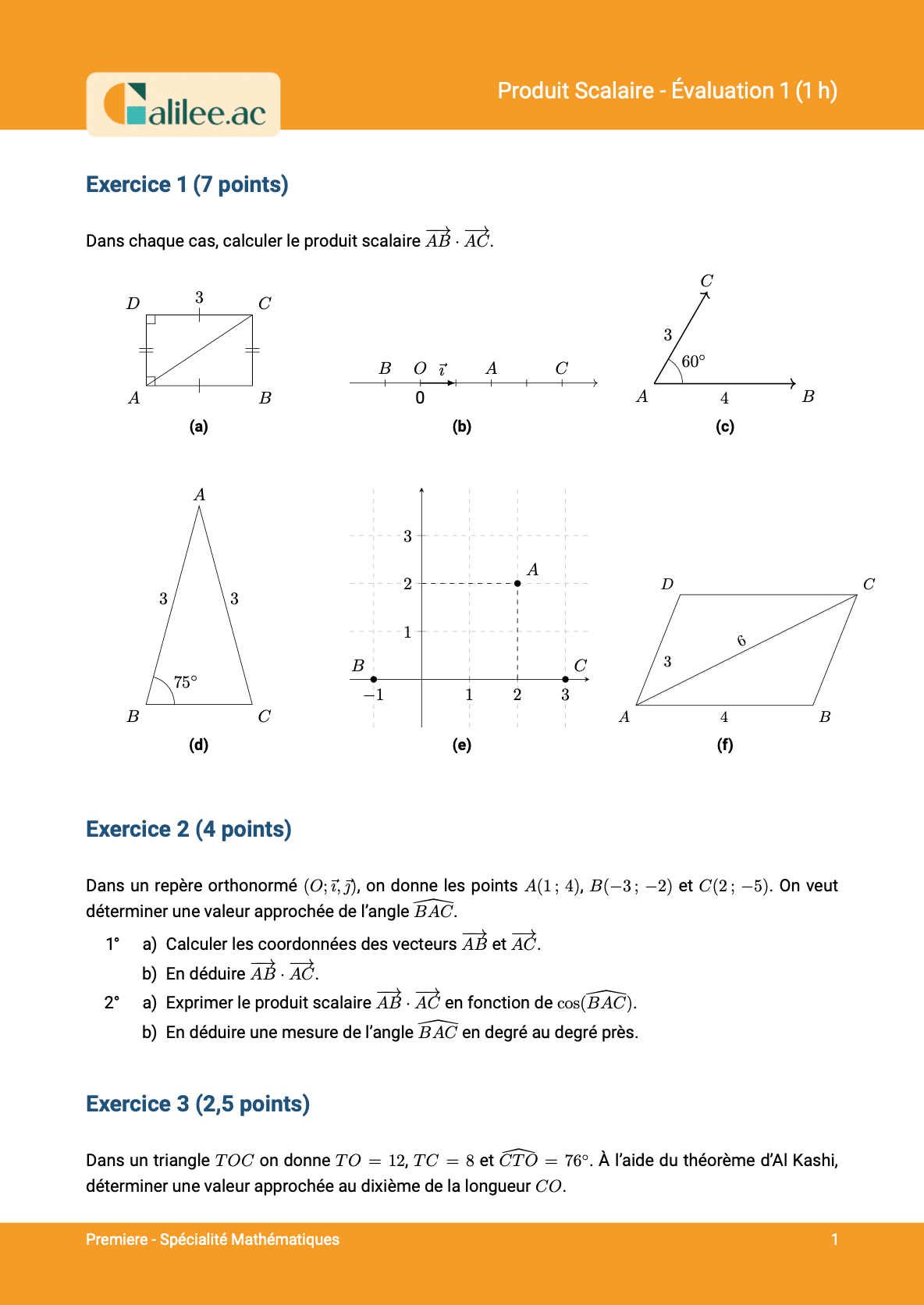
Allons-y, mes amis, nous allons voir deux formules ultra importantes qui permettent de calculer des produits scalaires quand on n'a pas les angles dans des triangles quelconques. On s'y met tout de suite. Les deux formules qui s'affichent à ma gauche sont essentielles pour calculer les produits scalaires dans le cas de triangles quelconques, c'est-à-dire des triangles pour lesquels vous n'avez pas d'emblée qu'ils sont des triangles particuliers, c'est-à-dire des triangles isocèles ou rectangles. C'est utile dans les paragraphes à la technique pour utiliser ces deux formules.

Explication des formules

La technique pour utiliser ces deux formules est de se dire : "Bon, là je vous ai donné deux produits scalaires \(AB\) et \(BC\), on va commencer par faire \(AB \cdot BC\) et ensuite on va faire \(AB \cdot AC\)." Vous voyez que ces deux configurations de vecteurs et que pour chacune des configurations de vecteurs, il y a une des deux formules qui va mieux marcher. Le problème, c'est que tant que vous n'avez pas un œil qui est bien entraîné, c'est compliqué de savoir laquelle des deux formules marche. Donc, ce que je vous recommande de faire, c'est au brouillon d'écrire les deux formules. La première formule donne donc un demi de \(AB + BC\) au carré - \(AB^2 - BC^2\). La deuxième formule donne un demi de \(AB^2 + BC^2 - (AB - BC)^2\). Une fois que j'ai écrit ça, je vais me demander lesquelles de ces longueurs je connais.

Application des formules

Ce que je connais très facilement, c'est \(AB\) et \(BC\). Donc, dans ces deux formules, je connais au moins deux des trois valeurs. La question, c'est est-ce que je connais la troisième, c'est-à-dire est-ce que je connais \(AB + BC\)? Ne faites surtout pas l'erreur de dire que la norme de \(AB + BC\) c'est la norme de \(AB\) plus la norme de \(BC\). La norme de \(AB + BC\) c'est la norme du vecteur \(AC\). Donc, cette longueur, en fait, je la connais. Donc, vous voyez que dans la première formule, vous connaissez \(AB + BC\), vous connaissez la norme de \(AB\) et vous connaissez la norme de \(BC\). Donc, en fait, vous connaissez les trois, donc vous n'avez pas besoin d'utiliser la deuxième formule. Vous pouvez utiliser la première. La première formule dit que ça fait un demi de la norme de \(AB + BC\) au carré, donc \(3^2 - 7^2 - 3^2\), et ça donne un demi de -44, donc ça donne -22. Voilà pour le premier produit scalaire. Remarquez une chose, qu'est-ce qui se serait passé si on avait essayé de calculer \(AB - BC\)? \(AB - BC\) donne \(AB + (-BC)\), donc \(AB - BC\) donne le vecteur \(AC\). Sauf que je n'ai aucune idée de sa longueur, donc je n'aurais jamais pu calculer cette longueur. Donc, je me serais retrouvé bloqué dans une formule, je connaissais 1, 2 mais pas le troisième. On commence ici \(AB \cdot AC\), donc je réécris mes deux formules. \(AB \cdot AC\) c'est au choix : 1. Un demi de la norme de \(AB + AC\) au carré - la norme de \(AB^2 - AC^2\) 2. Un demi de la norme de \(AB^2 + AC^2 - (AB - AC)^2\) Encore une fois, la norme de \(AB\) et la norme de \(AC\) sont faciles à calculer. La norme de \(AB\) est 7 et la norme de \(AC\) est 3. Donc, dans les deux formules, je pars avec deux nombres que je connais. La question qu'on va se poser, c'est est-ce que \(AB + AC\) est plus facile à calculer que \(AB - AC\)? Ne faites surtout pas l'erreur de dire que la norme de \(AB + AC\) au carré c'est tout simplement la norme de \(AB\) au carré plus la norme de \(AC\) au carré. C'est la norme non pas de \(2AB + AC\) mais la norme de \(AB + AC\). Donc, est-ce que \(AB + AC\) donne un vecteur que vous pouvez reconnaître? \(AB + AC\) donne le vecteur \(BC\). Donc, quand je fais \(AB + AC\), ça me donne le vecteur \(BC\). Est-ce que je connais sa longueur? Clairement pas du tout. Par contre, \(AB - AC\), d'après vous, donne \(AB + BC\), car \(-AC + BC\) donne \(AB\). Donc, quand je fais \(AB - AC\), c'est en fait comme si je calculais ce vecteur \(AB\). Et \(AB\) je connais sa longueur, elle fait 2. Donc, en utilisant la deuxième formule et non pas la première, j'ai bien un demi de \(7^2 + 3^2 - 2^2\), et ça donne 27.

Conclusion

En résumé, vous avez les deux formules. Dans chacun des cas, vous écrivez les deux formules. Dans chacun des cas, vous aurez toujours deux éléments connus, \(AB\) et \(BC\). La question, c'est est-ce que je connais la somme ou la différence? Est-ce que j'ai plutôt envie de voir la somme de mes deux vecteurs ou est-ce que j'ai plutôt envie de faire la différence? Et en fait, ça, on pourrait le savoir dès le début. Vous n'avez pas besoin de vous embêter à recopier les formules. Vous vous dites juste : "Est-ce que la somme ça me donne quelque chose? Si la somme ne donne rien, alors forcément c'est la différence." On vous a mis des petits exercices en dessous, vous allez prendre du plaisir. J'ai confiance en vous, vous êtes très bons.