Livre
3. Calculer la norme d'un vecteur
Conditions d'achèvement
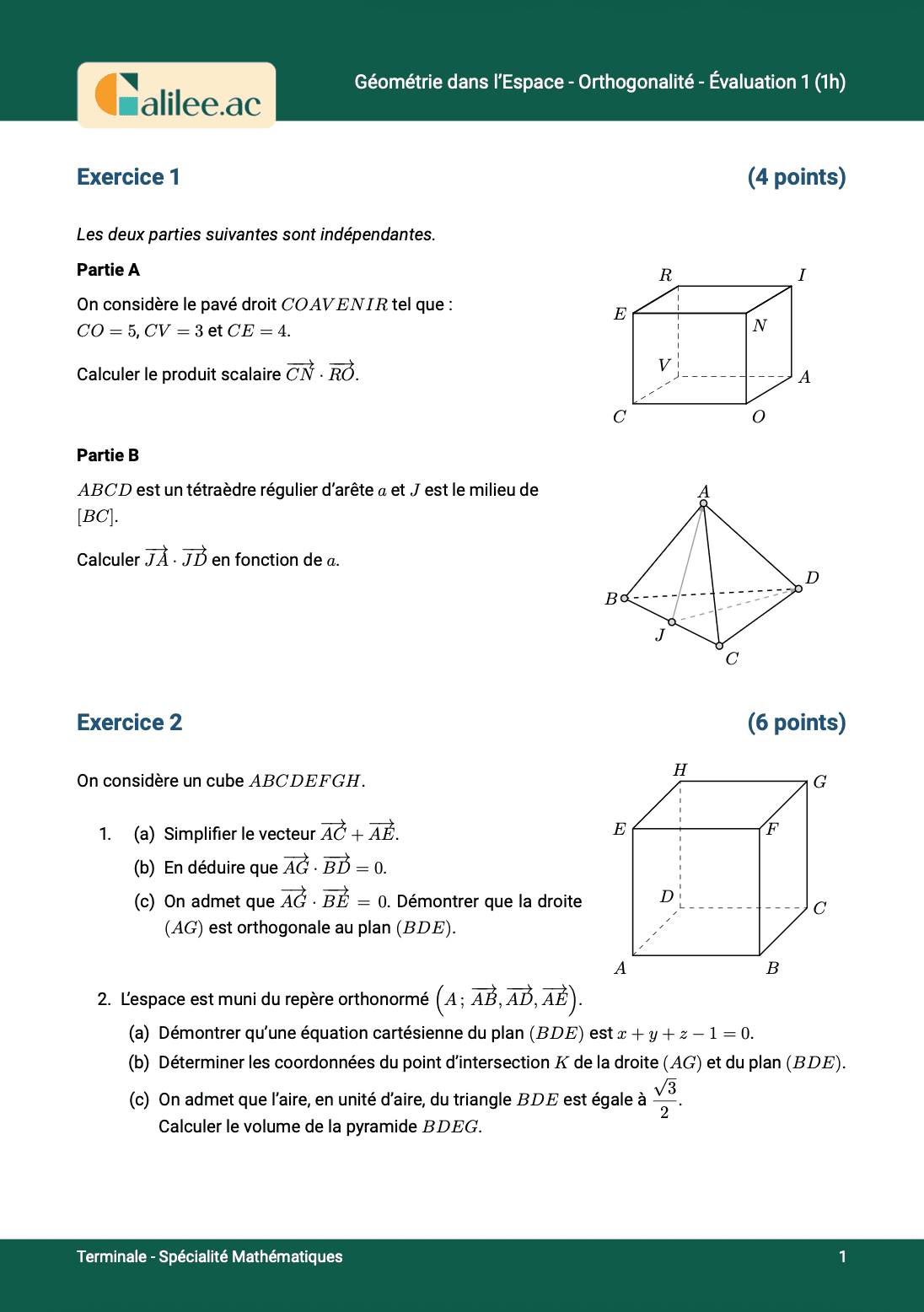
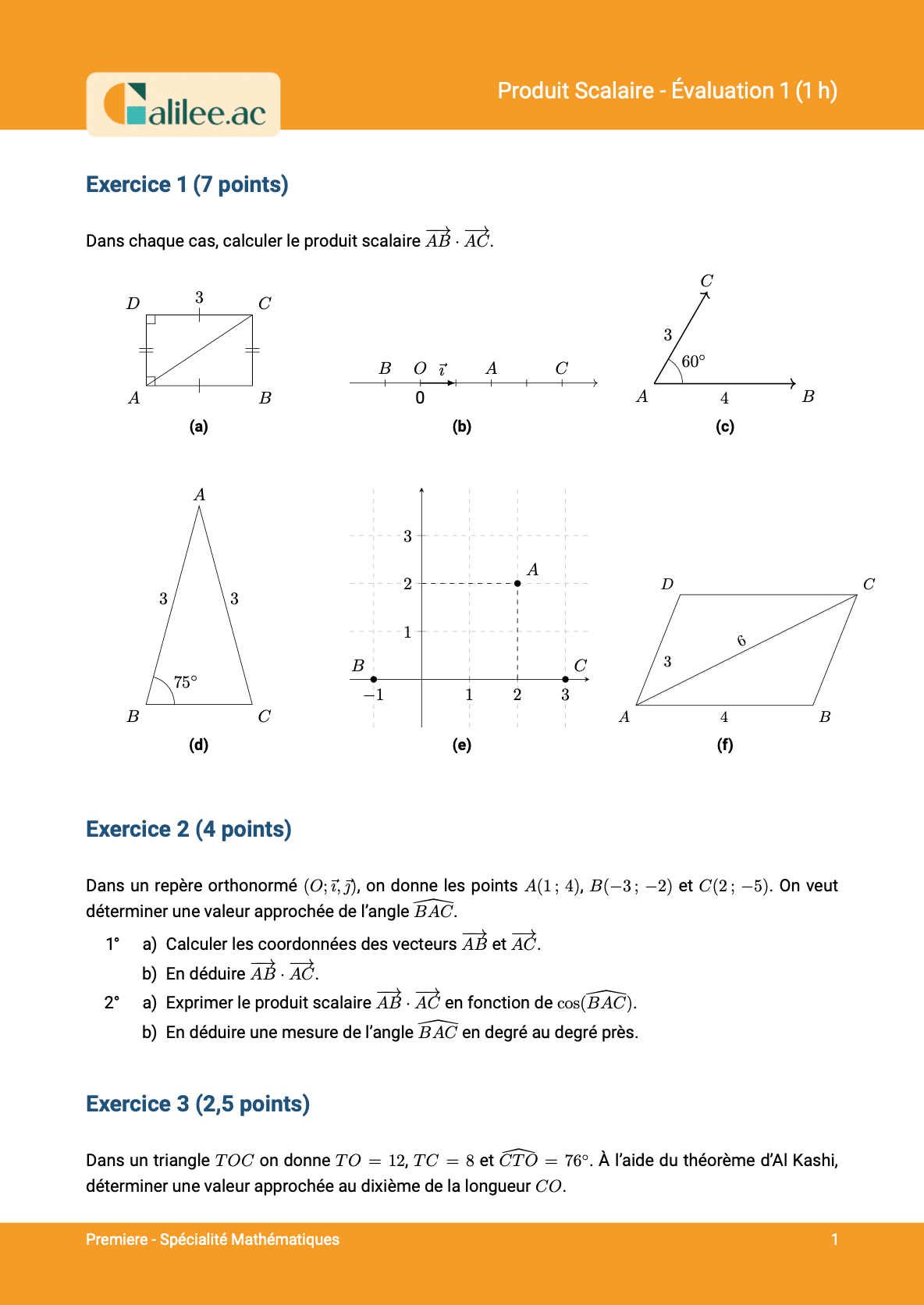
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on regarde vite fait comment calculer la norme d'un vecteur à partir de ses coordonnées. C'est parti !Formule de la norme d'un vecteur
Pour calculer la norme d'un vecteur à partir de ses coordonnées, il faut que vous maîtrisiez cette formule : la norme est égale à la racine carrée de la somme des carrés des coordonnées. En notation mathématique, cela donne : \[ \text{Norme} = \sqrt{x^2 + y^2} \] Cette formule provient du théorème de Pythagore.Application de la formule
Prenons un exemple. Supposons que nous ayons un vecteur avec des coordonnées \(x = 3\) et \(y = 4\). La norme de ce vecteur est donc : \[ \text{Norme} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 \] C'est aussi simple que cela.Calcul de la norme d'un vecteur à partir de ses points
Prenons une version légèrement différente. Supposons que nous ayons un vecteur \(AB\) et que nous ne connaissions pas ses coordonnées. Il va d'abord falloir que vous les calculiez. Pour cela, vous savez que les coordonnées du vecteur \(AB\) sont \(x_B - x_A\) et \(y_B - y_A\). Supposons que \(x_B = 5\), \(x_A = 1\), \(y_B = 1\) et \(y_A = 2\). Les coordonnées du vecteur \(AB\) sont donc \(-6\) et \(-1\). Maintenant, nous pouvons utiliser la formule de la norme : \[ \text{Norme} = \sqrt{(-6)^2 + (-1)^2} = \sqrt{36 + 1} = \sqrt{37} \] Et voilà, c'est fini. Cette formule est à noter sur votre fiche car elle est très utile et vous avez tendance à l'oublier. Nous vous avons mis une ou deux applications pour vous entraîner.Recrue
Visiteur anonyme
7 pts