Livre
1. Calculer un produit scalaire grâce aux normes et l'angle
Conditions d'achèvement
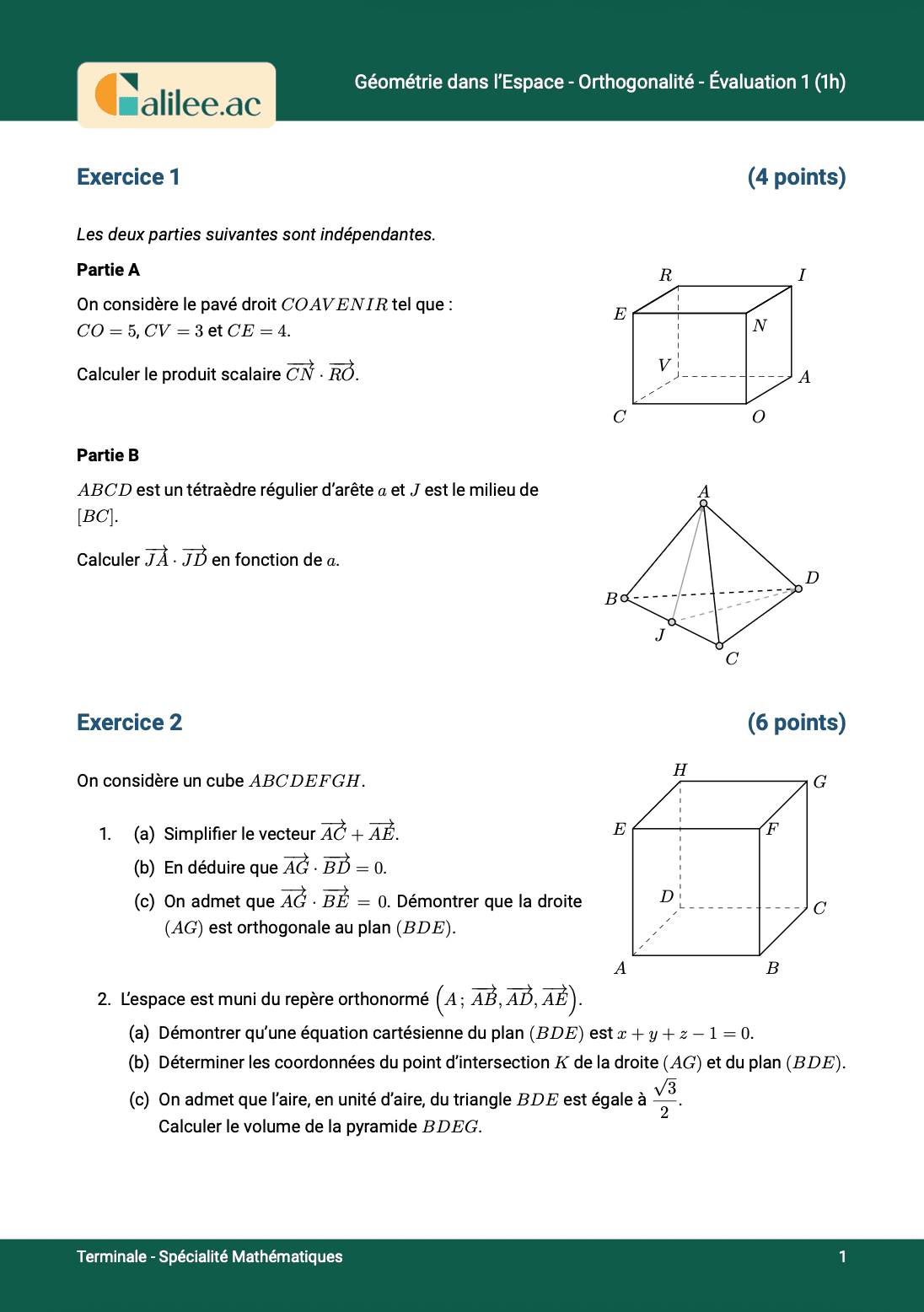
Exercice
1
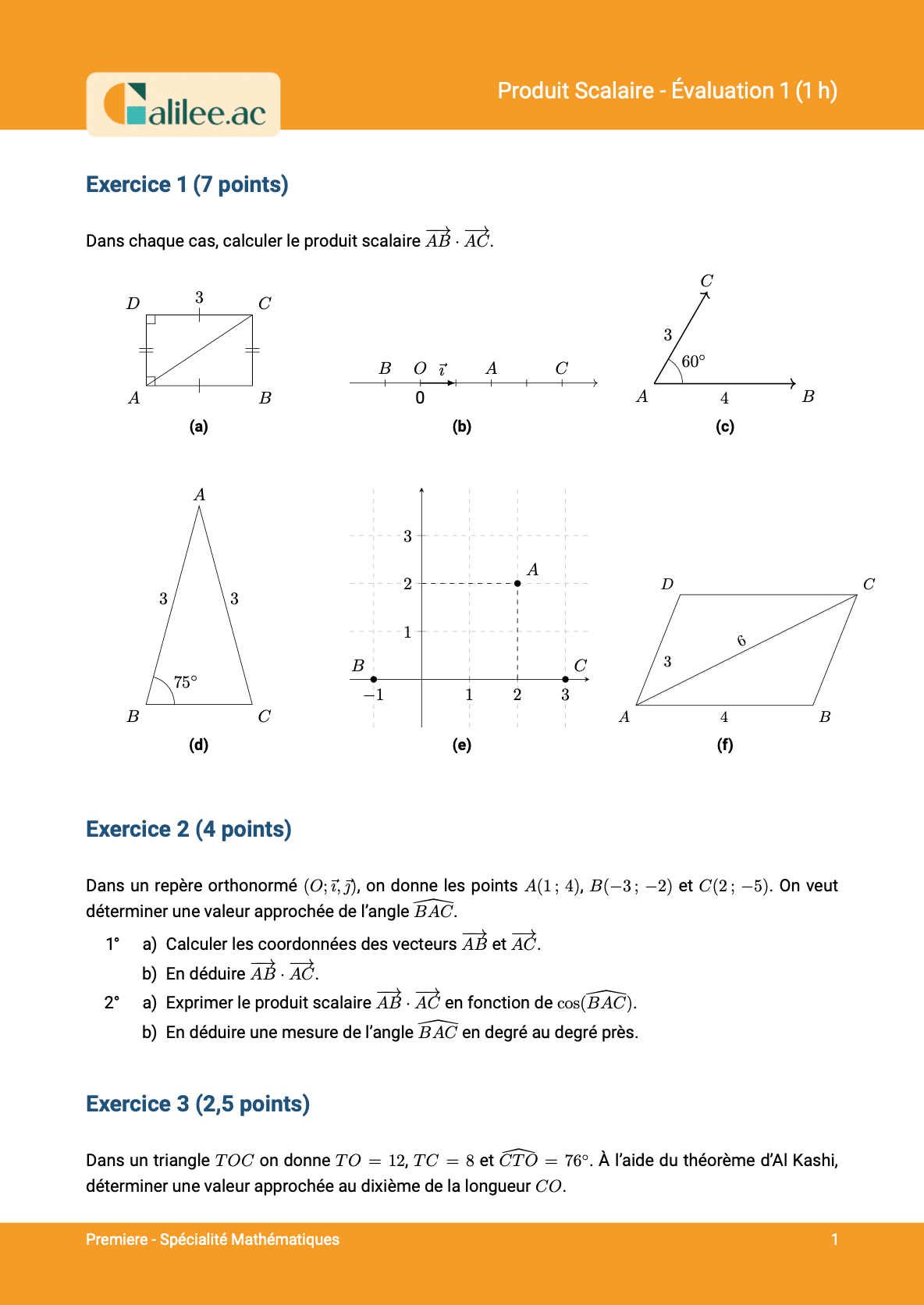
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour apprendre à utiliser la plus fameuse des formules avec le produit. Ce qui nous intéresse, c'est celle des normes et de l'angle. On y va quand vous voulez. Quand on veut calculer un produit scalaire, le premier réflexe à avoir c'est d'utiliser la formule qui s'affiche là : \(||u|| \times ||v|| \times \cos(\theta)\), où \(||u||\) et \(||v||\) sont les normes des vecteurs et \(\theta\) est l'angle entre eux. Vous allez voir que la principale difficulté elle est au niveau de l'angle.Exemple 1
Prenons ce carré de côté 2. Je vous demande de calculer le produit scalaire entre les vecteurs AB et AD. Donc ce que je vous demande c'est à chaque fois de faire apparaître les vecteurs au moins au début. Donc AB est là, AD est là. L'angle que je recherche c'est celui qui est entre AB et AD, donc c'est cet angle là. Donc je reprends la formule : \(||AB|| \times ||AD|| \times \cos(\theta)\). L'angle ici vaut combien ? On est dans un carré, un carré a un angle droit, donc c'est 90 degrés ou en radians, \(\pi/2\). Le cosinus de \(\pi/2\) est zéro, donc ça me fait \(2 \times 2 \times 0\), ça me fait zéro. C'est pas étonnant puisque quand deux vecteurs sont perpendiculaires, le produit scalaire vaut 0.Exemple 2
Passons à un cas un peu plus difficile. Calculons le produit scalaire entre les vecteurs AB et BC. Les deux vecteurs ne sont pas alignés, donc vous ne pouvez pas mesurer l'angle directement. Le seul moyen que vous avez de mesurer l'angle, c'est de prendre le vecteur BC et de le déplacer juste à côté de AB pour qu'ils soient alignés. On se rend compte que AB et BC sont colinéaires et dans le même sens, ça veut dire que l'angle entre les deux est de zéro degré. Donc ici je vais avoir un cosinus de 0. Les normes de AB et BC sont toujours de 2, donc ça fait \(2 \times 2 \times 1\), ça me fait 4.Exemple 3
Enchaînons avec encore plus de difficultés. Calculons le produit scalaire entre les vecteurs AB et CD. Pour mesurer l'angle, je prends le vecteur CD et je le déplace de manière à ce qu'il soit aligné avec AB. Le problème c'est que si je le déplace comme ça, ils sont opposés. Donc il faut que je prenne le vecteur CD et je le déplace de manière à ce qu'ils soient alignés dans le même sens. Maintenant, quel est cet angle là ? C'est 180 degrés, donc en radians, c'est \(\pi\). Donc là je vais avoir \(\cos(\pi)\). Les normes de AB et CD sont toujours de 2, donc ça fait \(2 \times 2 \times -1\), ça me fait -4.Conclusion
Retenez bien que pour mesurer l'angle entre deux vecteurs, il faut absolument que vous les mettiez tête à tête. On vous a mis des exercices pour vous entraîner. Bonne chance !Nouvelle recrue
Visiteur anonyme
1 pts