Livre
9. Tracer la tangente en un point d'une courbe
Conditions d'achèvement
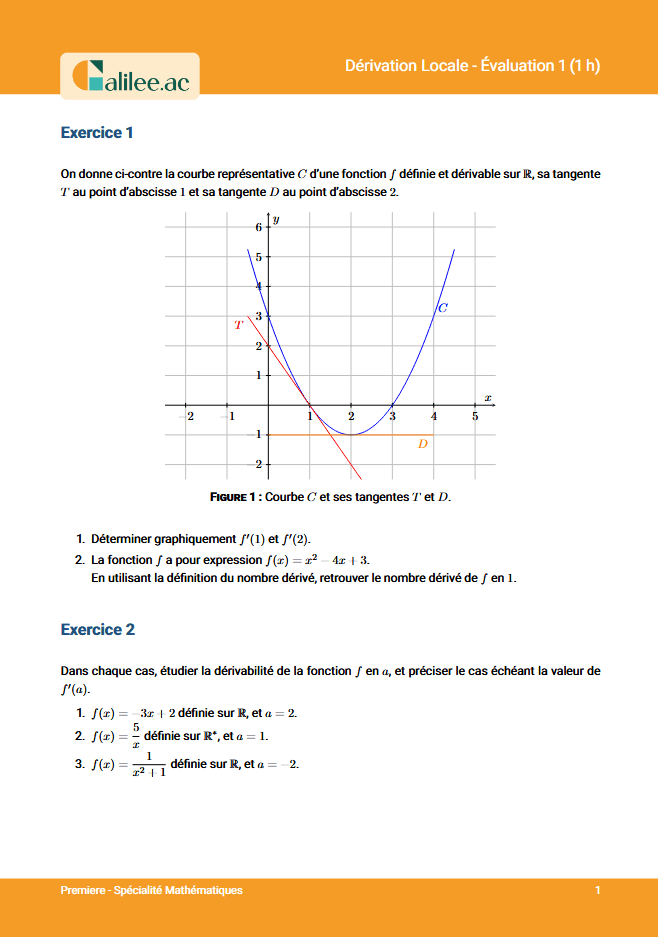
Exercice
1
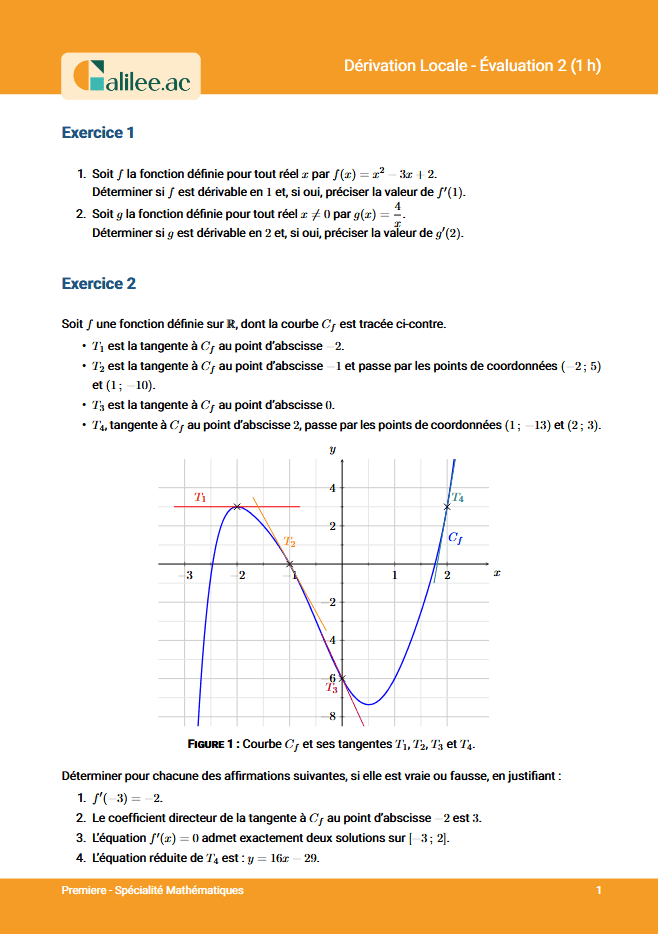
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
On est parti pour tracer la tangente à l'équation. Alors, on vous donne une fonction et on vous demande de tracer la tangente à cette fonction. Pour tracer la tangente de la fonction, il faut d'abord que vous obteniez l'équation de la tangente. La formule pour avoir l'équation de la tangente est \(y = f'(x) \cdot (x - a) + f(a)\). Donc, pour pouvoir exploiter cette formule, il vous faut deux choses : \(f'(a)\) et \(f(a)\).Calcul de l'équation de la tangente
Supposons que \(f'(a) = 2\) et \(f(a) = 1\). Avec ces valeurs, nous pouvons calculer l'équation réduite de la tangente, c'est-à-dire l'équation sous la forme des équations que l'on connaît pour les droites, c'est-à-dire \(y = mx + p\). Donc, en remplaçant \(f'(a)\) et \(f(a)\) dans la formule, on obtient \(y = 2 \cdot (x - 1) + 1\), ce qui se simplifie en \(y = 2x - 2 + 1\), soit \(y = 2x - 1\).Tracé de la tangente
Pour tracer la tangente, il faut comprendre que l'équation d'une droite affine est toujours de la forme \(y = mx + p\), où \(m\) est le coefficient directeur et \(p\) l'ordonnée à l'origine. L'ordonnée à l'origine est le point pour lequel la tangente va croiser l'axe des ordonnées. Ici, la tangente va croiser l'axe des ordonnées en \(y = -1\). Le coefficient directeur donne la pente de la tangente. Si le coefficient directeur est 2, cela signifie que pour chaque unité que l'on avance sur l'axe des abscisses, on monte de deux unités sur l'axe des ordonnées. Ainsi, pour tracer la tangente, on part du point d'intersection avec l'axe des ordonnées, on avance d'une unité sur l'axe des abscisses et on monte de deux unités sur l'axe des ordonnées. On obtient ainsi un autre point de passage de la tangente. En reliant ces deux points, on obtient la tangente à la fonction au point d'abscisse 1. Voilà, vous savez tracer l'équation d'une tangente. À vous de jouer maintenant !Nouvelle recrue
Visiteur anonyme
0 pts