Introduction
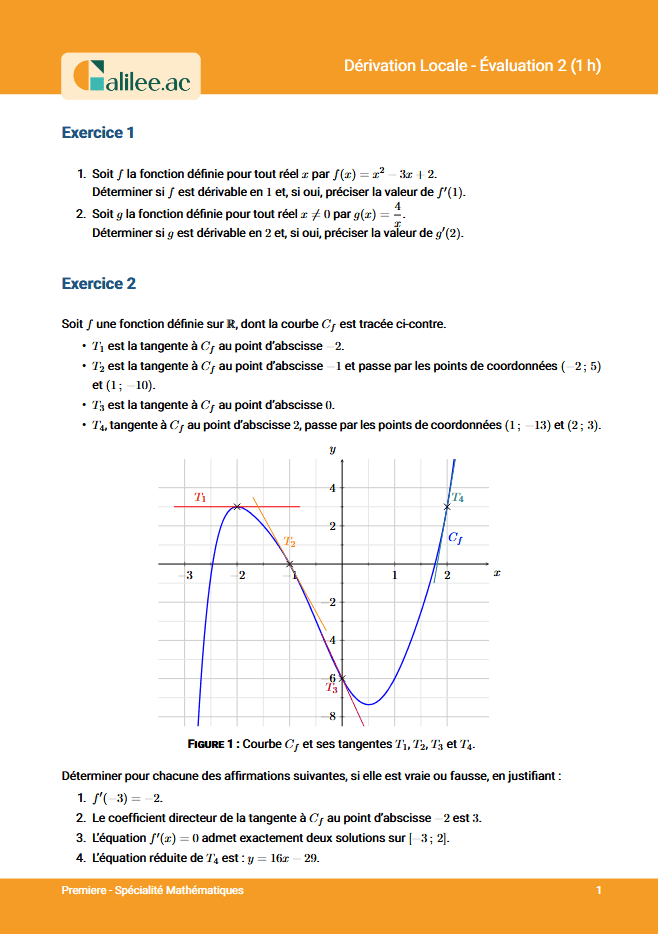
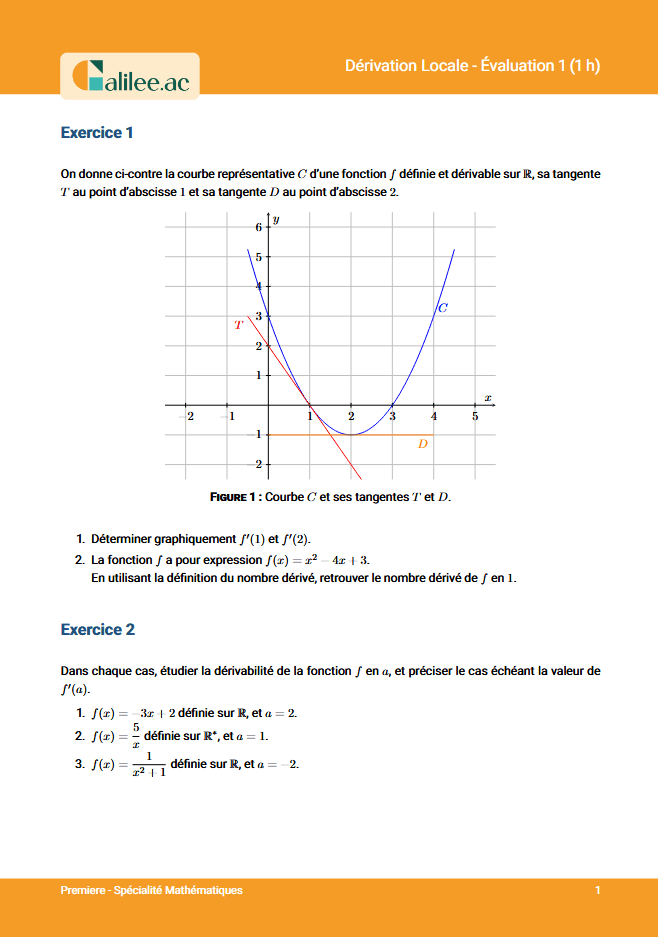
Pour déterminer graphiquement les équations des tangentes à une fonction, vous allez avoir besoin de deux choses. Premièrement, vous devez savoir lire la dérivée et, deuxièmement, vous devez connaître par cœur l'équation suivante : \(y = f'(a) \cdot (x - a) + f(a)\).
Premier exemple avec le point M
Prenons un premier exemple avec le point M. Pour trouver l'équation de la tangente au point M, vous allez avoir besoin du nombre dérivé au point M ainsi que de la formule précédente. Pour calculer le nombre dérivé graphiquement, il faut se souvenir que le nombre dérivé est le coefficient directeur de la tangente. Donc, si on vous donne une fonction et qu'on vous a tracé la tangente, pour connaître le nombre dérivé, vous avez juste à trouver le coefficient directeur de la droite qui est la tangente.
Pour calculer le nombre dérivé, on va prendre cette tangente et on va essayer de trouver un rectangle qui tombe sur des points précis. Par exemple, ce triangle que je dessine en bleu est parfait parce qu'on arrive pile au point M et pile à ce point là. Ensuite, on va déterminer la longueur verticale que je vais appeler \(\Delta y\) et la longueur horizontale que je vais appeler \(\Delta x\). Le coefficient directeur, c'est-à-dire \(f'(a)\), est égal à \(\Delta y / \Delta x\), c'est-à-dire la longueur verticale divisée par la longueur horizontale.
Deuxième exemple avec le point N
Prenons un deuxième exemple avec le point N. Pour le point N, il va nous falloir le nombre dérivé en -1, c'est-à-dire \(f'(-1)\), et il va nous falloir \(f(-1)\). Pour trouver \(f'(-1)\), on peut utiliser la technique du triangle rectangle ou on peut prendre deux points sur la tangente et déterminer leurs coordonnées. Pour connaître le coefficient directeur de la droite, on va faire \(y_B - y_A / x_B - x_A\), c'est-à-dire l'ordonnée du deuxième point moins l'ordonnée du premier divisée par l'abscisse du deuxième point moins l'abscisse du premier.
Troisième exemple avec le point P
Pour le point P, on va devoir calculer \(f'(2)\) et \(f(2)\). Pour trouver \(f(2)\), on se place sur l'abscisse 2 et on regarde où est-ce que l'on arrive en ordonnée, on arrive à -1. Pour trouver \(f'(2)\), on regarde le coefficient directeur de la tangente au point 2. Cette droite est horizontale, donc le coefficient directeur de cette droite est 0. On peut donc utiliser la formule \(y = f'(2) \cdot (x - 2) + f(2)\) pour trouver l'équation de la tangente.