Livre
6. Trouver graphiquement la valeur du nombre dérivé
Conditions d'achèvement
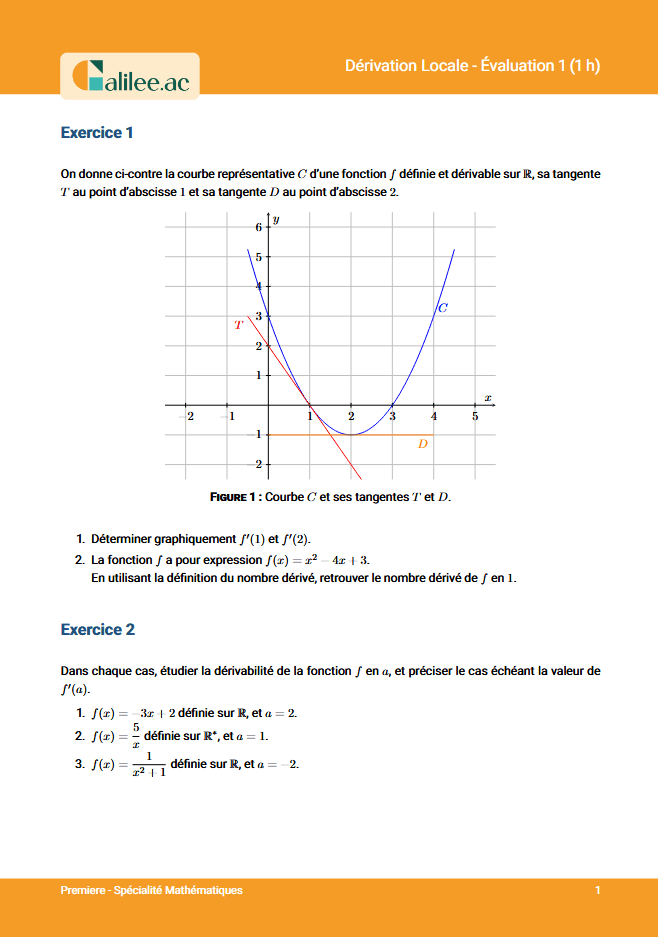
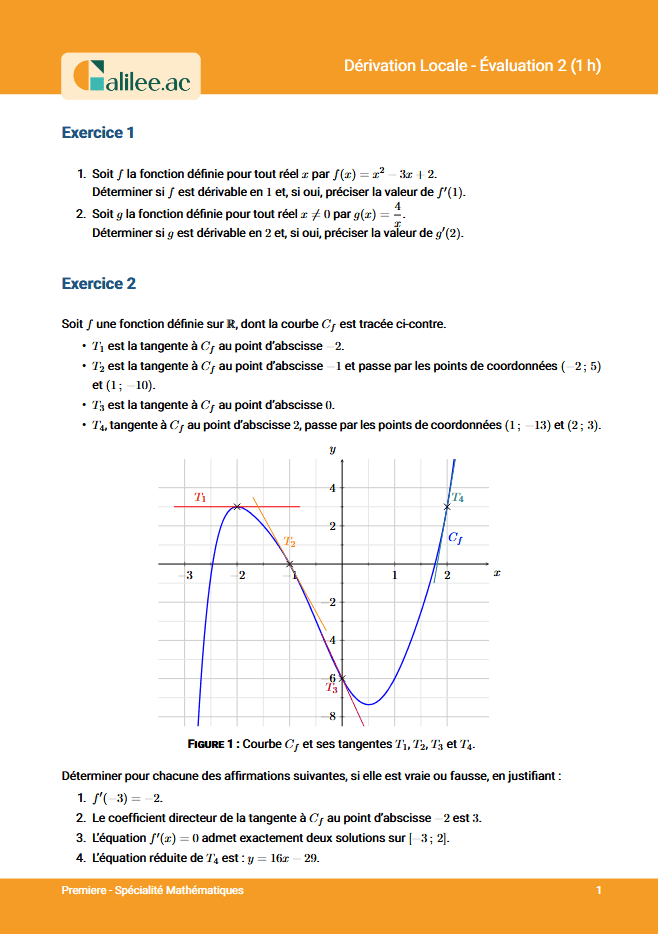
Exercice
1
Pour aller plus loin : Contrôles sur ce chapitre 🎯
PremièreRecommandé
Contrôle Dérivation Locale 1
Chapitres: Dérivation locale
Première spécialitéRecommandé
Contrôle Probabilités conditionnelles et dérivation locale - sujet 33
Chapitres: Probabilités Conditionnelles Dérivation locale
Première spécialitéRecommandé
Contrôle Dérivation locale et trigonométrie - sujet 18
Chapitres: Dérivation locale Trigonométrie
Première spécialitéRecommandé
Contrôle Second Degré, Fonctions Trigo et Dérivation Locale
Chapitres: Polynômes du second degré Trigonométrie ...
Première spécialitéRecommandé
Contrôle Dérivation locale et produit scalaire - sujet 32
Chapitres: Dérivation locale Produit scalaire
Première spécialitéRecommandé
Contrôle Dérivation et second degré - sujet 19
Chapitres: Dérivation globale Dérivation locale ...
Première spécialitéRecommandé
Contrôle Second degré, dérivation, probabilités et suites - sujet 31
Chapitres: Polynômes du second degré Dérivation locale ...
Première spécialitéRecommandé
Contrôle Trigonométrie et dérivation locale - sujet 24
Chapitres: Trigonométrie Dérivation locale
PremièreRecommandé
Contrôle Dérivation Locale 2
Chapitres: Dérivation locale
Première spécialitéRecommandé
Contrôle Dérivation locale - sujet 3
Chapitres: Dérivation locale
Première spécialitéRecommandé
Contrôle Dérivation locale - sujet 4
Chapitres: Dérivation locale
Première spécialitéRecommandé
Contrôle Dérivation et suites - sujet 38
Chapitres: Dérivation locale Suites arithmétiques et géométriques ...
le nombre dérivé de 1 égale à 8?
Introduction
Déterminons graphiquement le nombre dérivé. Une fois que vous savez le faire avec l'expression de la dérivée, vous allez apprendre à le faire juste en regardant le graphique de la courbe. Donc, je vous demande de me trouver le nombre dérivé de plusieurs points simples, notamment pour \(x = -5\), \(x = -2\) et \(x = 0\).Calcul du nombre dérivé pour \(x = -5\)
Pour trouver \(f'(-5)\), je me place en \(x = -5\), je trouve la tangente à la courbe à ce point et je détermine le coefficient directeur de cette tangente. Pour cela, je propose une technique qui marche relativement à tous les coups. Vous trouvez deux points pour lesquels votre tangente passe exactement. Par exemple, les points A et B. Les coordonnées de A sont \((-5, -1)\) et les coordonnées de B sont \((-4, 0)\). Ensuite, vous appliquez la formule \((y_B - y_A) / (x_B - x_A)\). Donc, \(f'(-5) = (0 - (-1)) / (-4 - (-5)) = 1\). On peut noter que \(f'(-5) = 1\).Calcul du nombre dérivé pour \(x = -2\)
Pour \(f'(-2)\), je me place en \(x = -2\). La tangente à la courbe à ce point est horizontale, donc son coefficient directeur vaut toujours 0. Donc, \(f'(-2) = 0\).Calcul du nombre dérivé pour \(x = 0\)
Pour \(f'(0)\), je me place en \(x = 0\). Je choisis deux points sur la tangente, par exemple A et B avec les coordonnées de A étant \((0, 0)\) et les coordonnées de B étant \((2, -2)\). J'applique la formule \((y_B - y_A) / (x_B - x_A)\). Donc, \(f'(0) = (-2 - 0) / (2 - 0) = -1\). En conclusion, le nombre dérivé peut être trouvé soit en utilisant le taux de variation et la limite lorsque vous avez l'expression de la fonction, soit en passant par le coefficient directeur de la tangente lorsque vous avez une représentation graphique.Nouvelle recrue
Invité
0 pts
