Livre
2. Dérivabilité en un point et calcul du nombre dérivé
Conditions d'achèvement
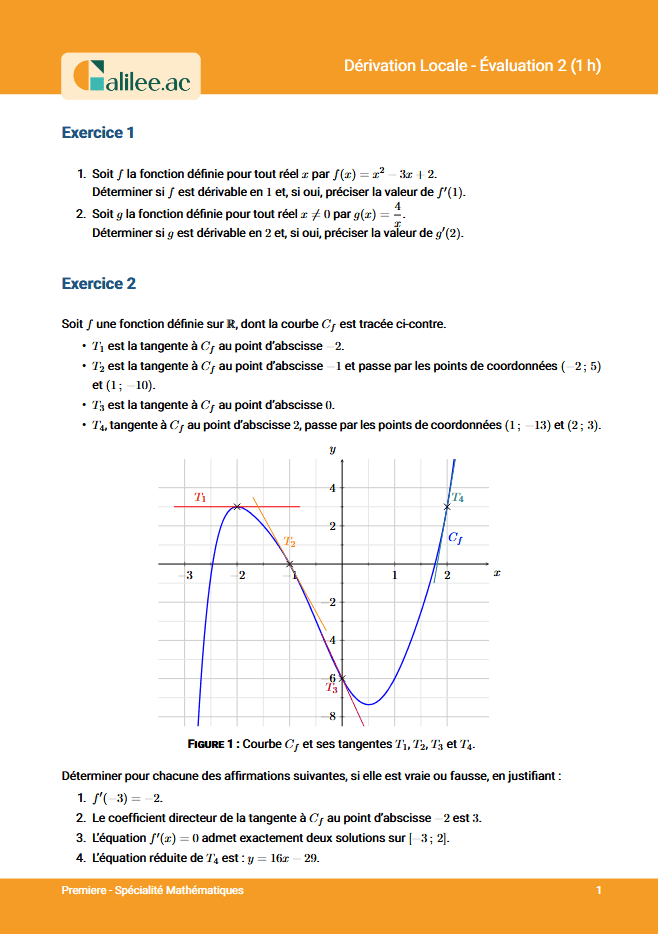
Exercice
1
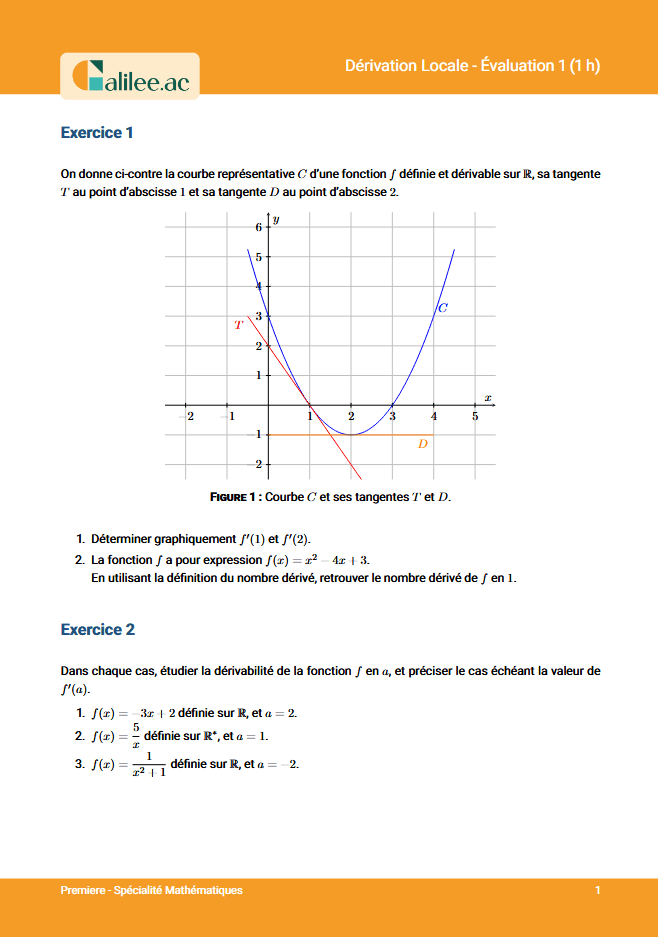
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Dans cette leçon, nous allons apprendre à calculer des dérivées et à déterminer si une fonction est dérivable en un point. Pour chaque cas, nous devons déterminer si la fonction est dérivable en \(a\) et donner son nombre dérivé. Nous allons utiliser trois fonctions pour illustrer cette technique de base.Procédure de calcul des dérivées
La procédure est la suivante : 1. Calculer le taux de variation entre \(a\) et \(a+h\). Cela revient à calculer \(f(a+h) - f(a) / h\). 2. Calculer la limite de ce que vous venez de trouver quand \(h\) tend vers zéro. 3. Si cette limite existe et est finie (par exemple, si cette limite vaut 3), alors vous avez trouvé \(f'(a)\), la dérivée de \(f\) en \(a\). Si la limite n'est pas finie, alors la fonction n'est pas dérivable en \(a\).Exemples de calcul des dérivées
Prenons par exemple la fonction \(f(x) = 2x^2 - 3\). Pour déterminer si cette fonction est dérivable en \(2\) et donner son nombre dérivé, nous suivons la procédure ci-dessus. 1. Nous calculons d'abord \(f(2+h) - f(2) / h\), ce qui donne \((2(2+h)^2 - 3) - (2(2)^2 - 3) / h = (2h^2 + 8h) / h\). 2. Ensuite, nous calculons la limite de ce que nous venons de trouver quand \(h\) tend vers zéro, ce qui donne \(2h + 8\). 3. Comme cette limite est finie et vaut \(8\), nous pouvons dire que la fonction \(f(x) = 2x^2 - 3\) est dérivable en \(2\) et que son nombre dérivé en \(2\) est \(8\). De la même manière, nous pouvons déterminer que la fonction \(f(x) = x + 3\) est dérivable en \(1\) et que son nombre dérivé en \(1\) est \(1\). En revanche, la fonction \(f(x) = \sqrt{x}\) n'est pas dérivable en \(0\), car la limite de \((\sqrt{h} - \sqrt{0}) / h\) quand \(h\) tend vers zéro est infinie.Conclusion
Il est important de maîtriser cette démarche pour calculer des dérivées et déterminer si une fonction est dérivable en un point. En pratiquant avec différents exemples, vous deviendrez de plus en plus à l'aise avec cette technique.Nouvelle recrue
Visiteur anonyme
0 pts