Livre
24. Démontrer que deux vecteurs sont colinéaires avec Chasles
Conditions d'achèvement
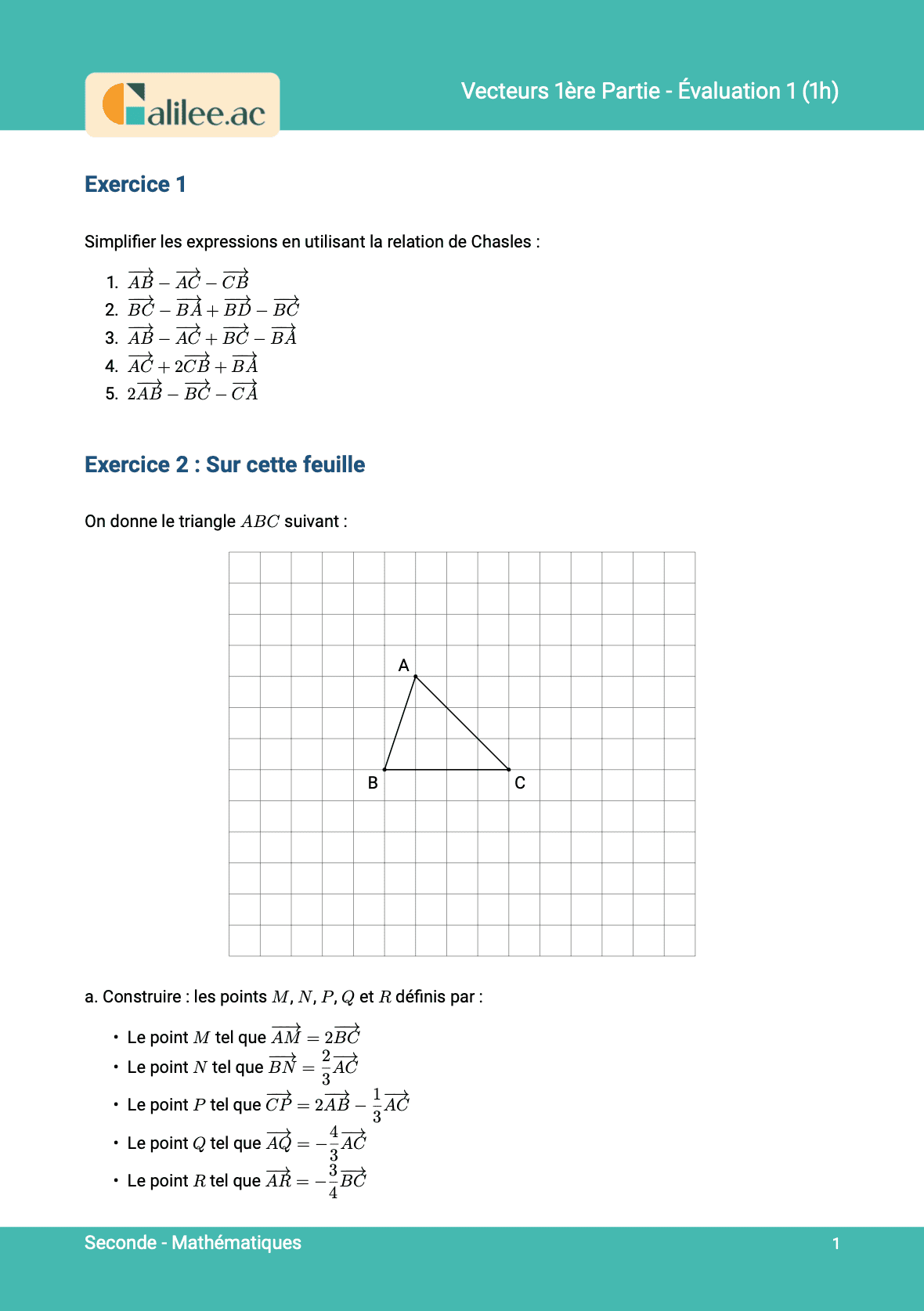
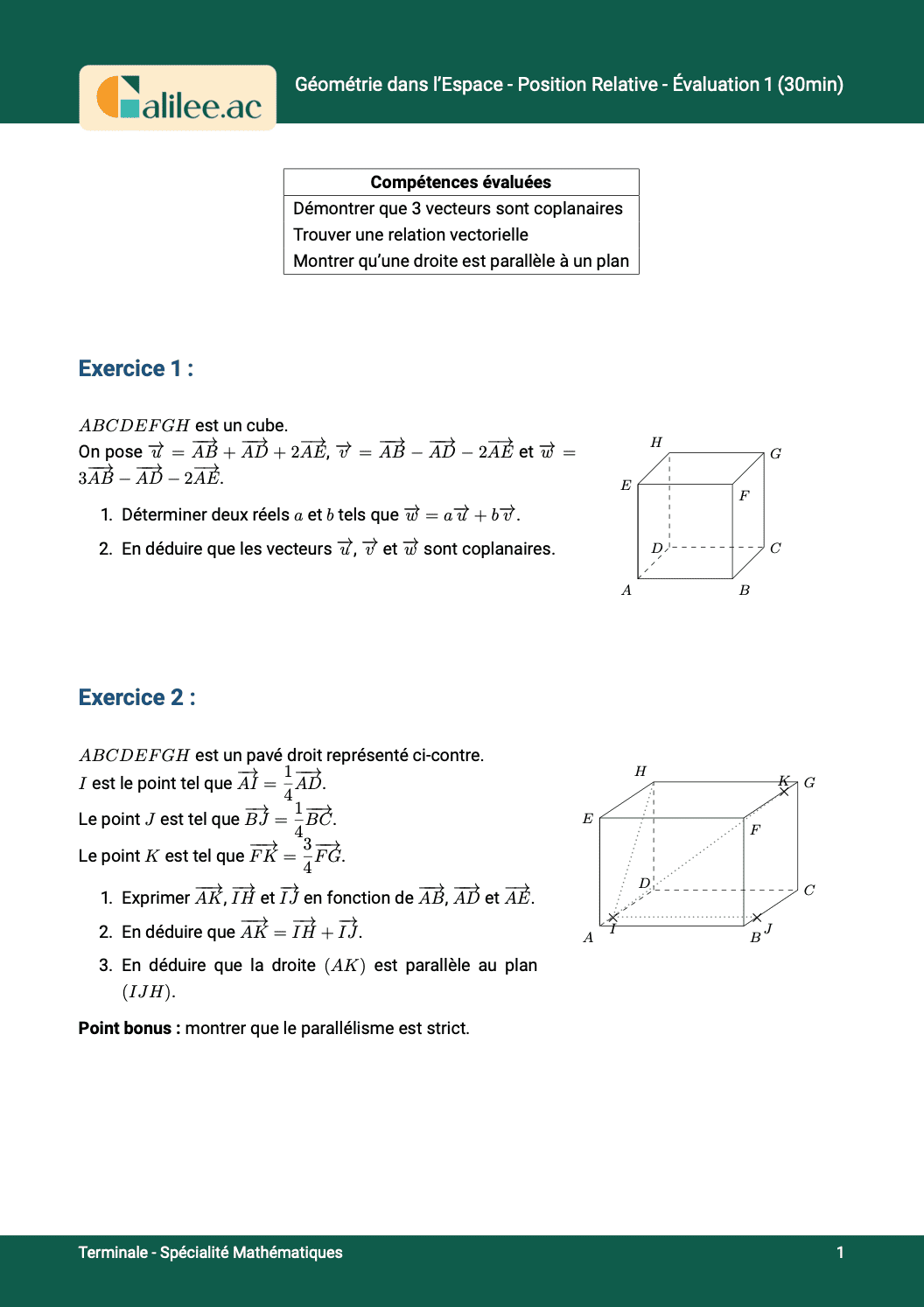
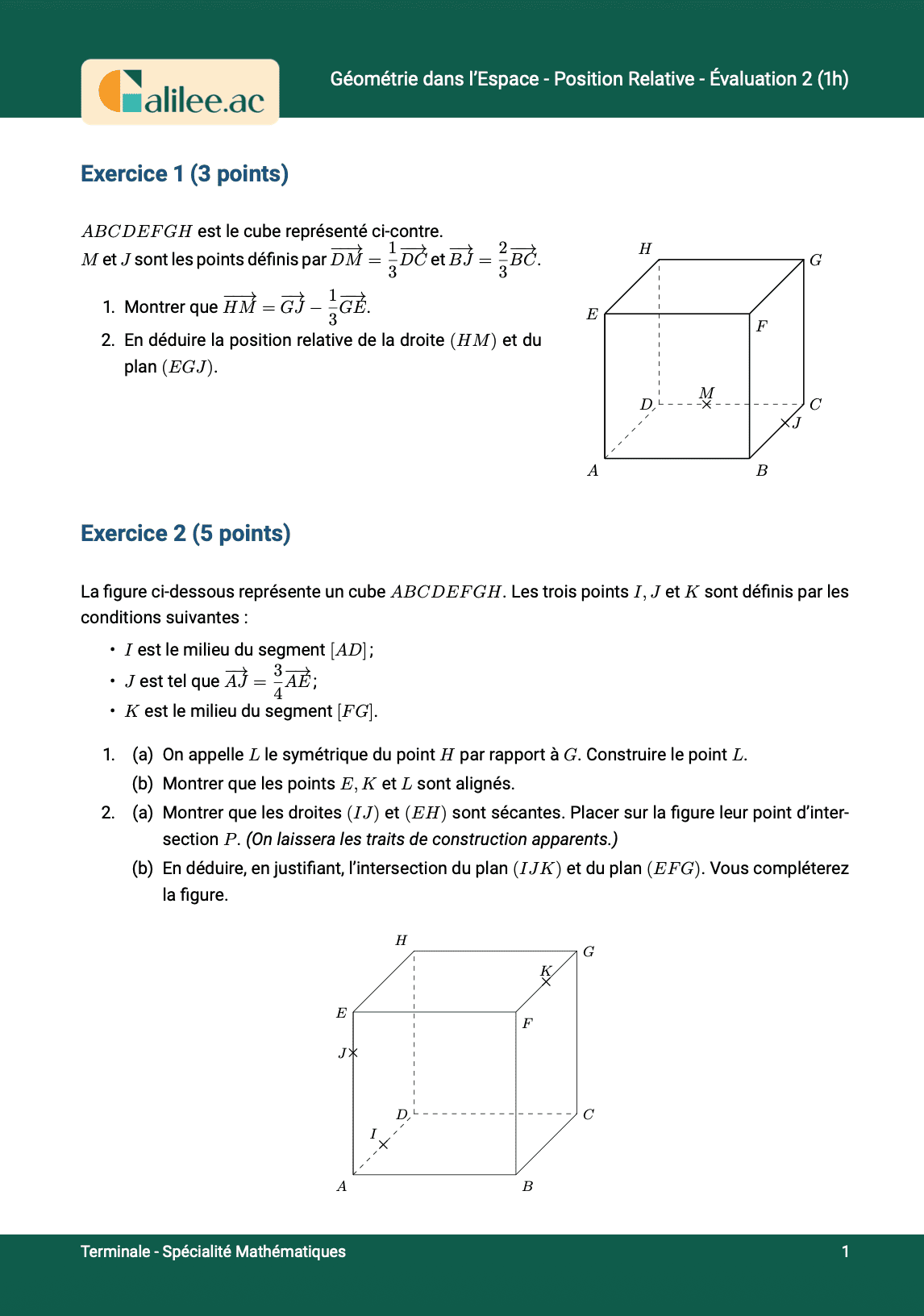
Exercice
1
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour voir un exercice qui a l'air vachement dur mais qui finalement n'est pas du tout. Il s'est montré que deux vecteurs sont collinéaires en utilisant des relations vectorielles qui sont données dans l'énoncé. On s'y met tout de suite.Comprendre les vecteurs collinéaires
La première chose qu'il faut que vous compreniez dans ces exercices là, c'est que c'est Chasles qui va vous sauver. Pourquoi ? Si vous voulez montrer que \(MN\) et \(BA\) sont collinéaires, sachant que \(MN\) et \(BA\) ont été définis comme ça, il va falloir partir de l'un de ces deux vecteurs. Par exemple, pour le vecteur \(MN\), vous allez le décomposer, travailler dessus et à la fin, si ils sont collinéaires, vous allez avoir écrit quelque chose fois \(BA\). Vous pouvez aussi choisir de faire exactement l'inverse : partir de \(BA\), le décomposer, travailler dessus et à la fin, vous voulez quelque chose fois \(MN\). D'ailleurs, je vous encourage fortement au brouillon à commencer par une technique et si ça ne marche pas, aller vers l'autre technique.Utiliser les relations vectorielles
Deuxième point, quand on vous donne un triangle, vous dis \(ABC\) est un triangle, faut vite mais est-ce que ça vaut le coup que je fasse un dessin ? En fait, quand on vous dit \(ABC\) est un triangle, c'est comme si on vous disait \(A\), \(B\) et \(C\) sont trois points. Parce qu'en fait, si aucune information dans un triangle, ce n'est pas un triangle rectangle, c'est un triangle isocèle, c'est un triangle quelconque. Autrement dit, \(ABC\) ce sont trois points, c'est tout ce qu'on sait. Est-ce que ça vaut le coup de faire un dessin pour ça ? Non. Ce qu'il faut que vous compreniez, c'est que ce genre d'exercice est vraiment du sud au cou. Je pars de \(MN\) et je veux arriver à \(BA\). Les relations qui m'intéressent, c'est celle-là et celle-là. Donc je réfléchis, comment est-ce que je peux casser \(MN\) pour me retrouver avec du \(BC\). Deux options : soit je fais une pause par le point \(C\), où je dis que \(MN = MC + CN\), parce que si je fais \(CN\), j'ai du \(2AC\), donc ça m'intéresse à me faire apparaître du point \(C\). Soit je dis que \(MN = MA + AN\), auquel cas je peux utiliser cette relation là. Peu importe le point de départ, on arrive exactement au bon résultat.Conclusion
Ce calcul là, il a l'air terrible mais vous êtes obligés d'être capable de le faire. C'est à dire que c'est embêtant, je suis d'accord avec vous, c'est un tripotage de vecteurs. Il faut être ultra bien sur le fait que, je ne sais pas, par exemple le \(+3AC\) ça fait \(-3CA\). Il faut être capable de faire du Chasles dans un sens, c'est à dire prendre un vecteur et le casser en deux vecteurs, mais il faut aussi être capable de prendre deux vecteurs et de les transformer en un seul. Il y a du boulot, qui reprend toutes les compétences d'avant. Ça, c'est ce qui vous attend au contrôle. Faites-le, ça vaut vraiment le coup. On vous a mis des exercices en dessous à vous de jouer.Nouvelle recrue
Visiteur anonyme
0 pts