Livre
23. Démontrer que 2 vecteurs sont colinéaires sans le déterminant
Conditions d'achèvement
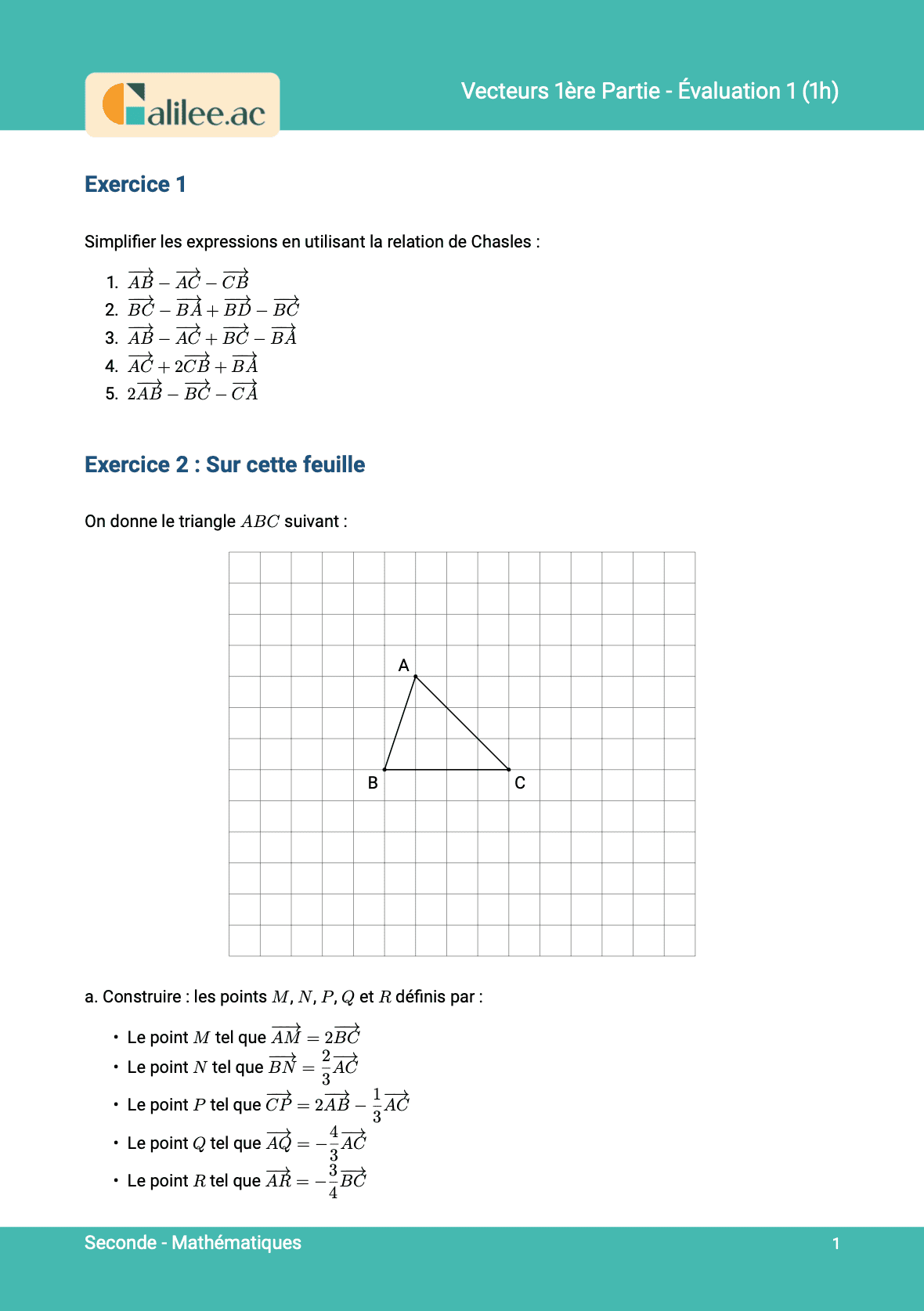
Exercice
1
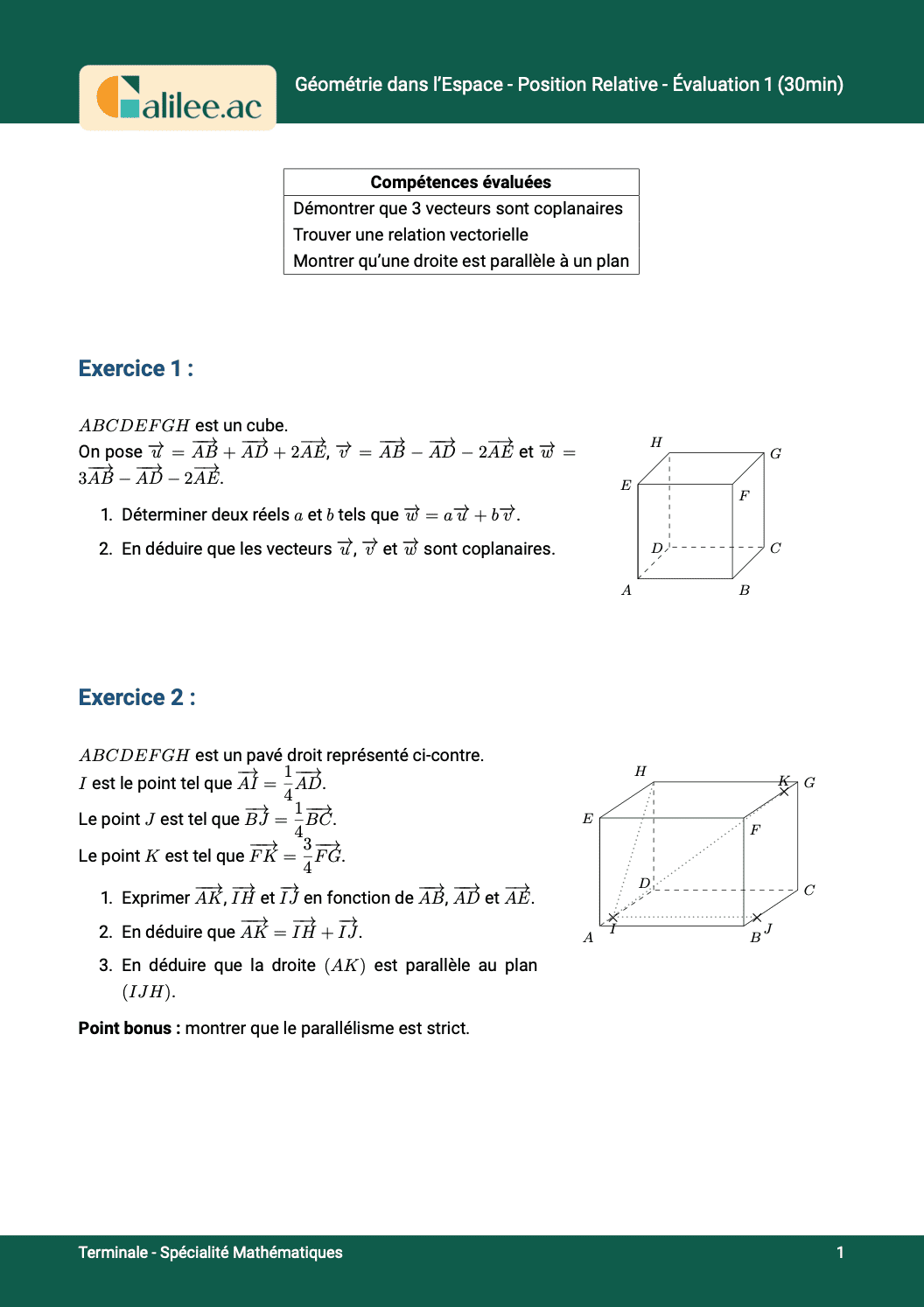
Exercice
2
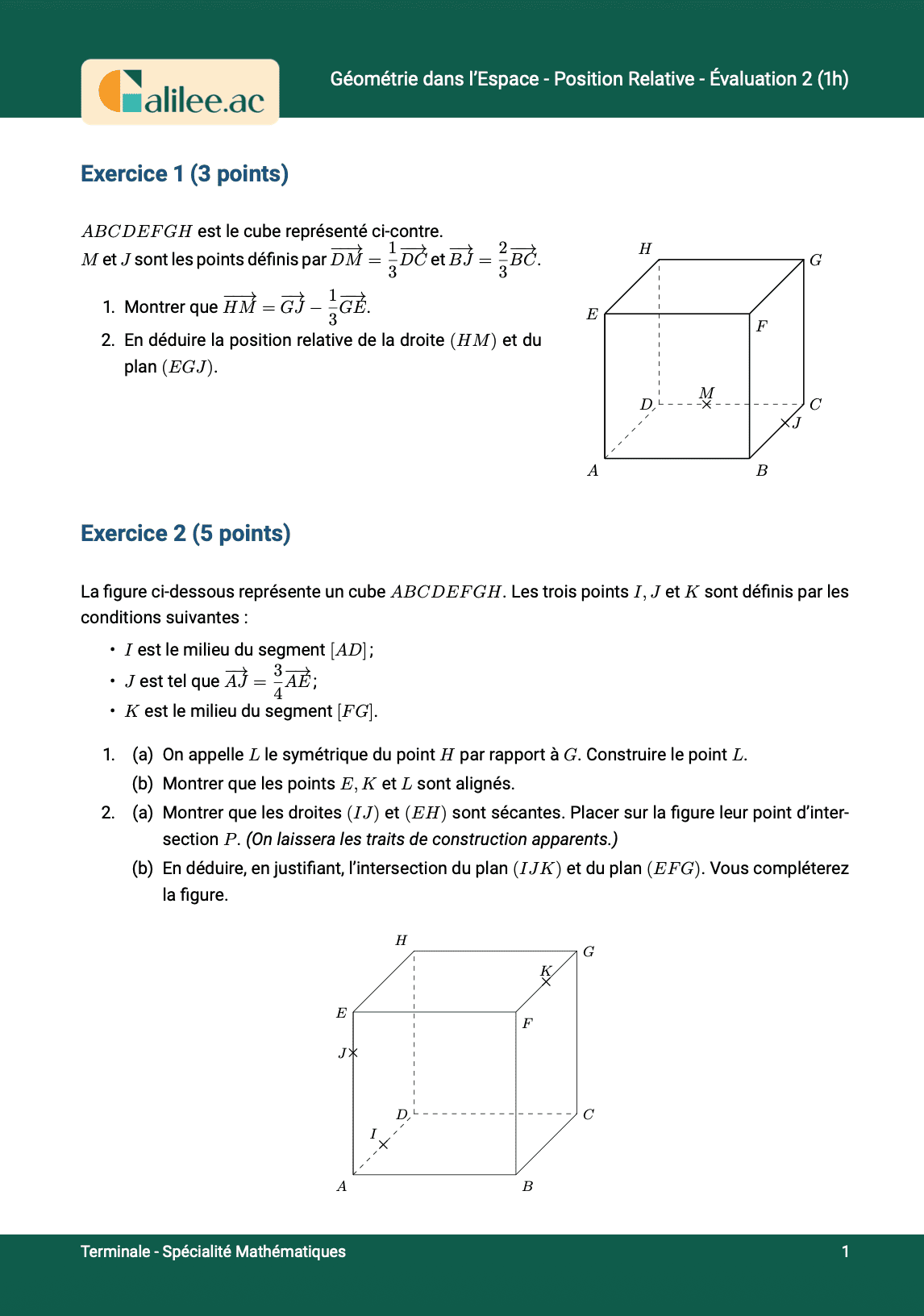
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour montrer que deux vecteurs sont collinéaires sans utiliser les déterminants mais en utilisant la proportionnalité. Donc, il faut revenir à ce que ça veut dire "collinéaires". Deux vecteurs sont collinéaires s'ils ont la même direction. Donc, si \(u\) et \(v\) sont collinéaires, ça veut dire que \(u\) et \(v\) sont proportionnels. Donc, il existe un certain nombre \(k\) qu'on ne connaît pas à l'avance, par exemple \(3, 2, 13, 40, -5\), tant que \(k\) n'est pas égal à zéro.Explication de la proportionnalité
Dans les cas où \(k = 1\), c'est à dire que \(u = v\), on a \(u\) qui est comme ça, \(v\) qui est comme ça. Si \(k = 2\), ça veut dire que \(u = 2 \times v\). J'ai \(v\) là, j'ai \(u\) qui est deux fois plus long. Si \(k = -1\), on va avoir \(u\) comme ça, \(v\) va être dans le sens opposé, et ainsi de suite. Dans tous les cas, on voit que ces vecteurs sont collinéaires.Résolution du problème
Donc, pour régler ce genre de problème, on va dire : s'ils sont collinéaires, alors \(u = k \times v\), et ensuite on passe aux coordonnées. Ça veut dire que le vecteur \(u = (3,7)\) est \(k\) fois le vecteur \(v = (-6,-14)\). Donc, ça veut dire que mon vecteur \(u = (3,7)\) est égal à \((-6k, -14k)\). Vous savez que quand vous avez un nombre qui multiplie un vecteur, il multiplie chaque coordonnée. Si le vecteur \(u = (3,7)\) est égal au vecteur \((-6k, -14k)\), ça veut dire que la première coordonnée de chacun de ces deux vecteurs est égale et que la deuxième coordonnée de chacun de ces deux vecteurs est égale. Donc, je me retrouve avec \(3 = -6k\) et \(7 = -14k\). Pour conclure, je vais isoler \(k\) dans chacune de ces équations. Si ça me donne le même résultat, c'est à dire si j'obtiens \(k\) dans les deux cas, alors \(u\) et \(v\) sont collinéaires. Si j'obtiens un \(k\) différent, ça veut dire qu'il me faudrait deux \(k\) différents pour avoir cette égalité, donc ils ne sont pas collinéaires. D'après la première équation, pour isoler \(k\), je vais tout diviser par \(-6\) et dans la deuxième, je vais tout diviser par \(-14\). Pourquoi je fais ça ? Parce que ça me permet de simplifier les \(-6\) et les \(-14\) pour avoir \(k\) tout seul d'un côté. Donc, dans le premier cas, je vais avoir \(k = 3 / -6\) et dans le deuxième cas, je vais avoir \(k = 7 / -14\). Alors, je finis mon calcul. \(3 / -6\) c'est comme \(3 / -3 \times 2\) et \(7 / -14\) c'est comme \(7 / -7 \times 2\). Du coup, je peux simplifier les \(3\) et les \(7\) et il me reste dans le premier cas \(k = 1 / -2\) donc \(-1/2\) et dans le deuxième cas \(1 / -2\) donc \(-1/2\). Il existe un unique \(k\) tel que cela soit vrai. Donc, \(u\) et \(v\) sont collinéaires. Mieux que ça, on peut même dire quel est le coefficient de proportionnalité, c'est à dire que au lieu de \(u = k \times v\), on a maintenant le droit d'écrire que \(u = -1/2 \times v\).Conclusion
En fait, cette méthode est beaucoup plus longue mais elle est beaucoup plus puissante que d'autres, parce qu'en plus de vous dire s'ils sont collinéaires, ce qui est le cas ici, ça vous donne aussi le coefficient de proportionnalité entre \(u\) et \(v\). On vous a mis des exercices en dessous, allez voir comment ça s'inscrit dans les exercices, allez jouer avec les exercices en dessous pour vous entraîner, pour vous graver la technique dans la tête. Vous êtes des champions, à vous de jouer.Nouvelle recrue
Visiteur anonyme
0 pts