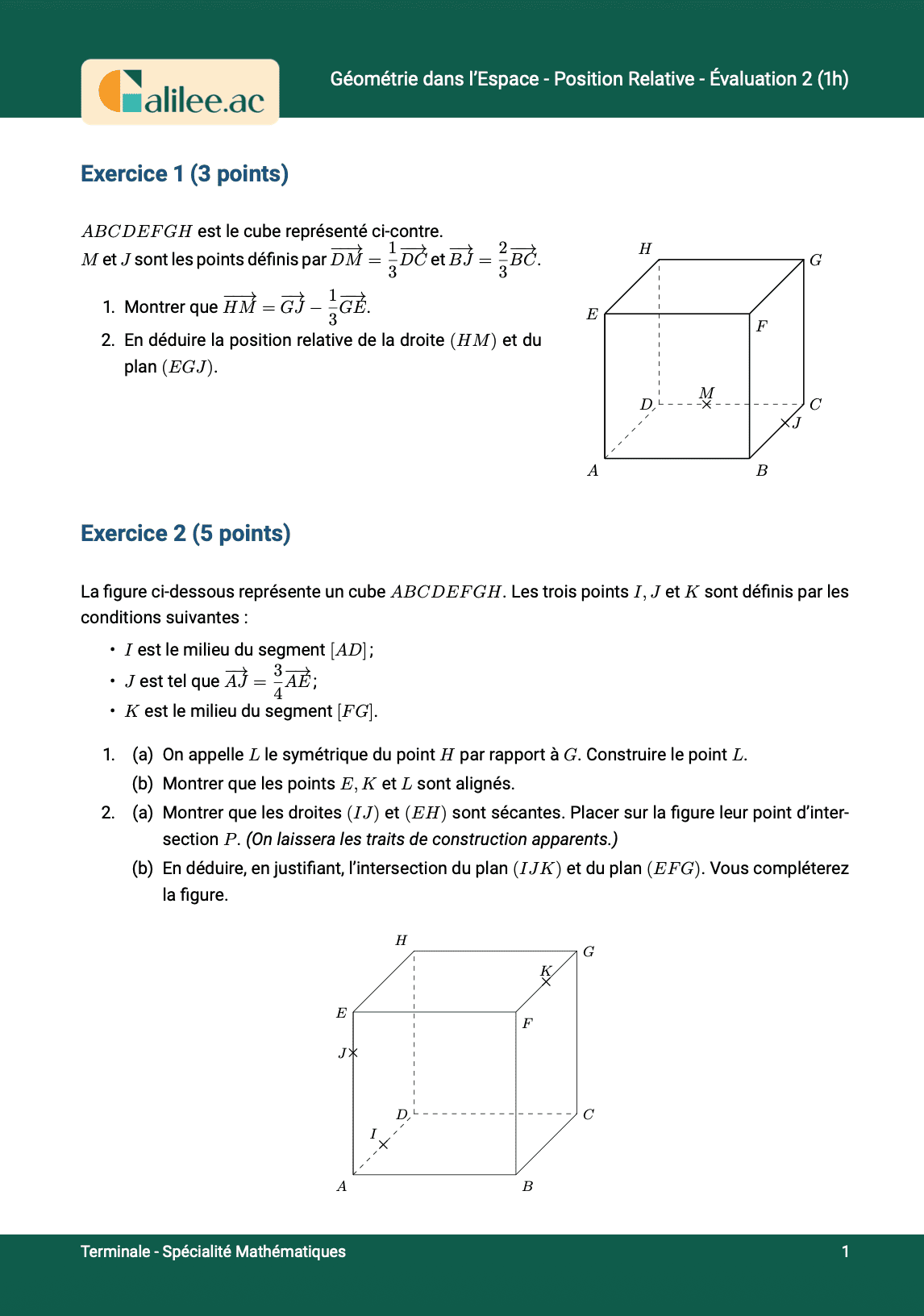
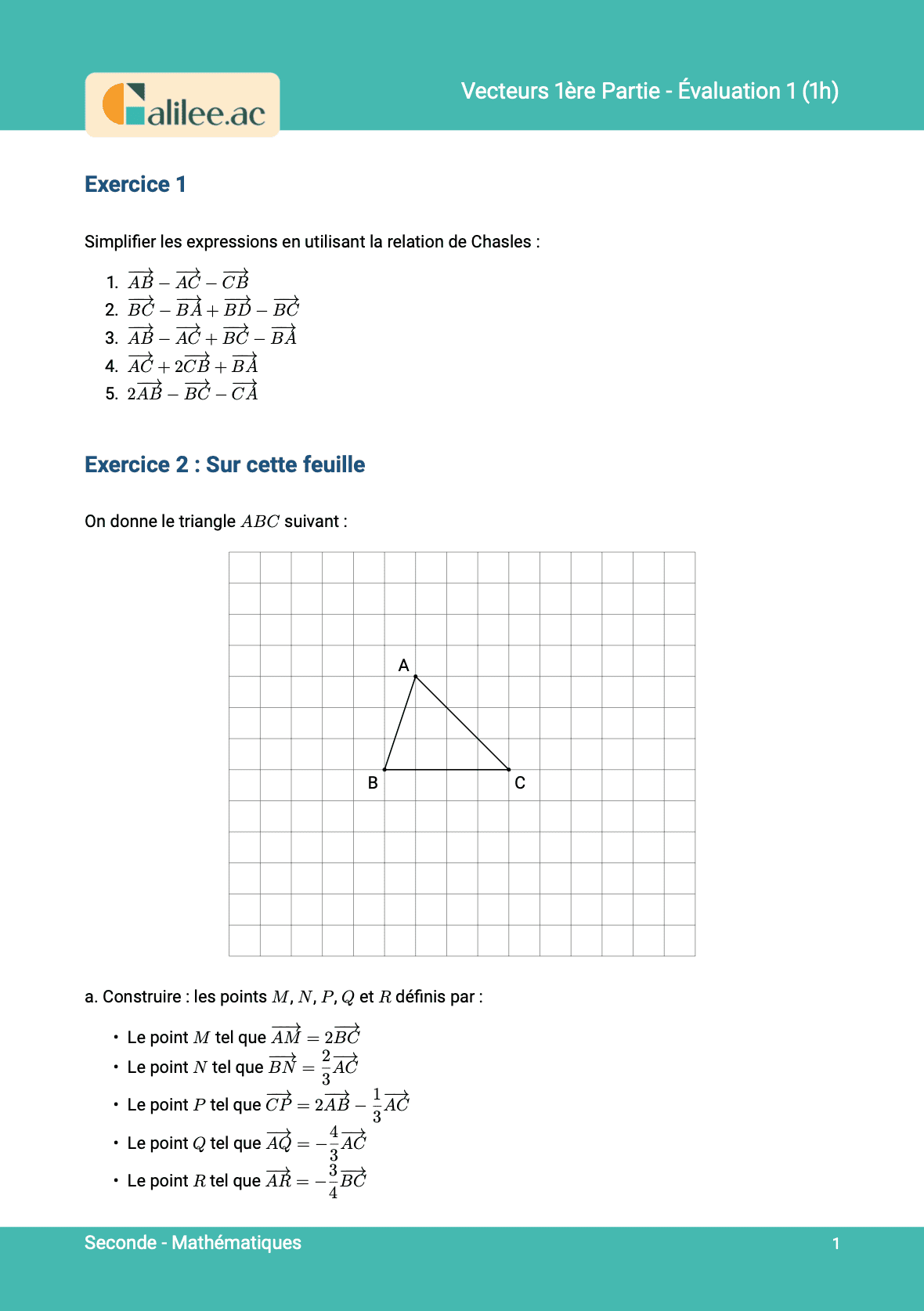
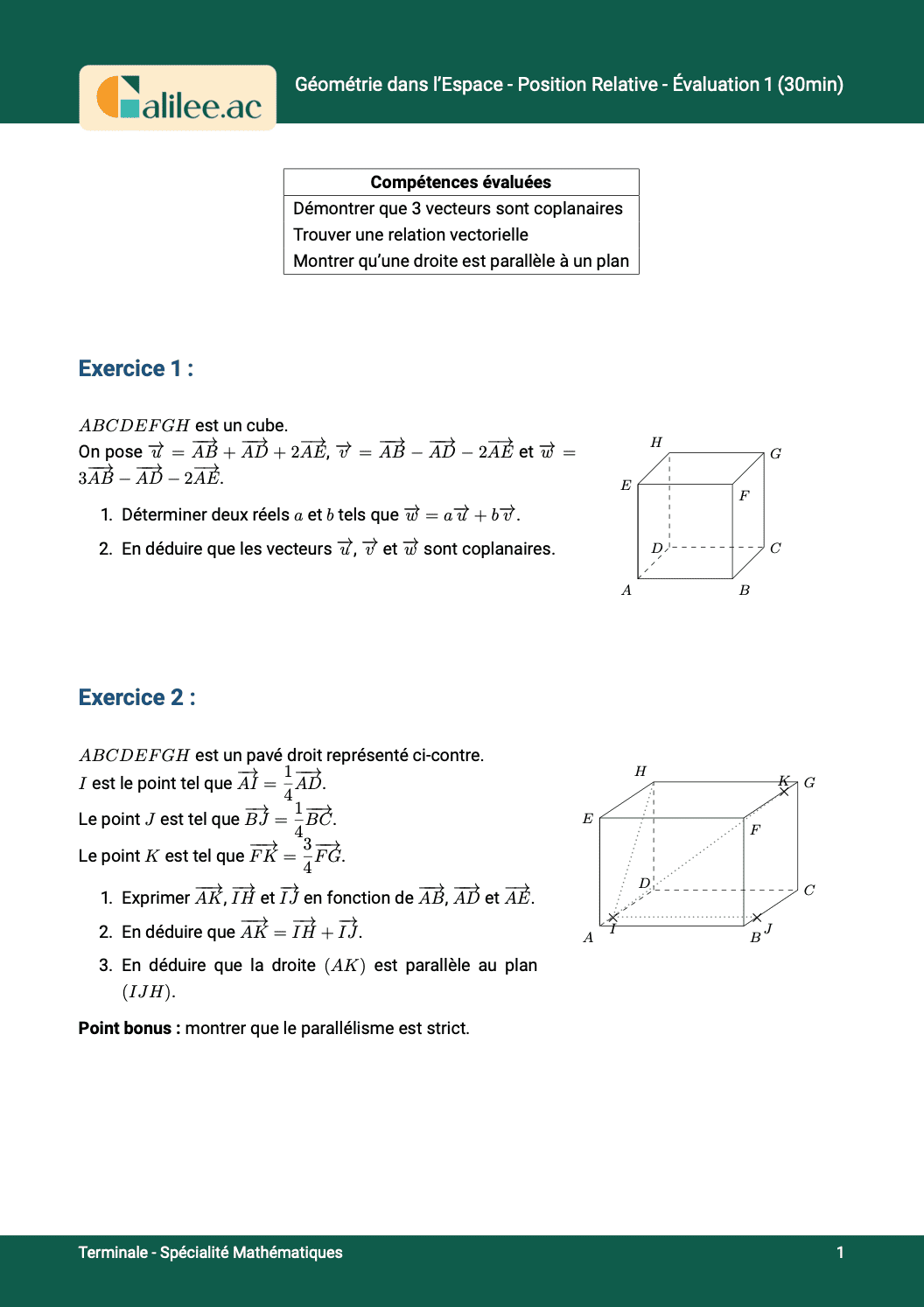
Livre
20. Reconnaître un parallélogramme à partir des coordonnées de points
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour utiliser les coordonnées des points d'un quadrilatère ABCD pour voir si c'est un parallélogramme ou non. On s'y met tout de suite.Rappel de la définition d'un parallélogramme
Pour rappel, si ABCD est un parallélogramme, ça veut dire que ABCD a ses côtés qui sont parallèles 2 à 2. Donc ça va donner quelque chose comme ça : A, B, C et D. Si c'est un parallélogramme, par définition, on a le vecteur AB qui est égal au vecteur DC, ou alors le vecteur AC est égal au vecteur BD. Donc, pour vérifier qu'un quadrilatère (un objet à quatre points, quatre côtés) est un parallélogramme, on va calculer d'abord les coordonnées du vecteur AB, puis les coordonnées du vecteur DC. On va vérifier si c'est la même chose. Si c'est la même chose, ça sera un parallélogramme.Calcul des coordonnées des vecteurs
Je commence avec les coordonnées de AB. Donc je vous rappelle la formule : \(x_B - x_A\) et \(y_B - y_A\). Donc \(5 - 1 = 4\) et \(6 - 2 = 4\). Voilà les coordonnées de AB. Les coordonnées de DC sont donc \(10 - 6 = 4\) et \(15 - 11 = 4\). Est-ce que le vecteur AB est égal au vecteur DC ? Évidemment, quand on regarde les coordonnées, absolument pas. Ces deux vecteurs ne sont pas égaux. Si ces vecteurs ne sont pas égaux, ça veut dire que les côtés opposés ne sont pas parallèles. Et si les côtés opposés ne sont pas parallèles et de même longueur, ça veut dire que ABCD n'est pas un parallélogramme. Et c'est terminé. On vous a mis des exercices en dessous, à vous de vous entraîner. Vous êtes prêts.Nouvelle recrue
Visiteur anonyme
0 pts