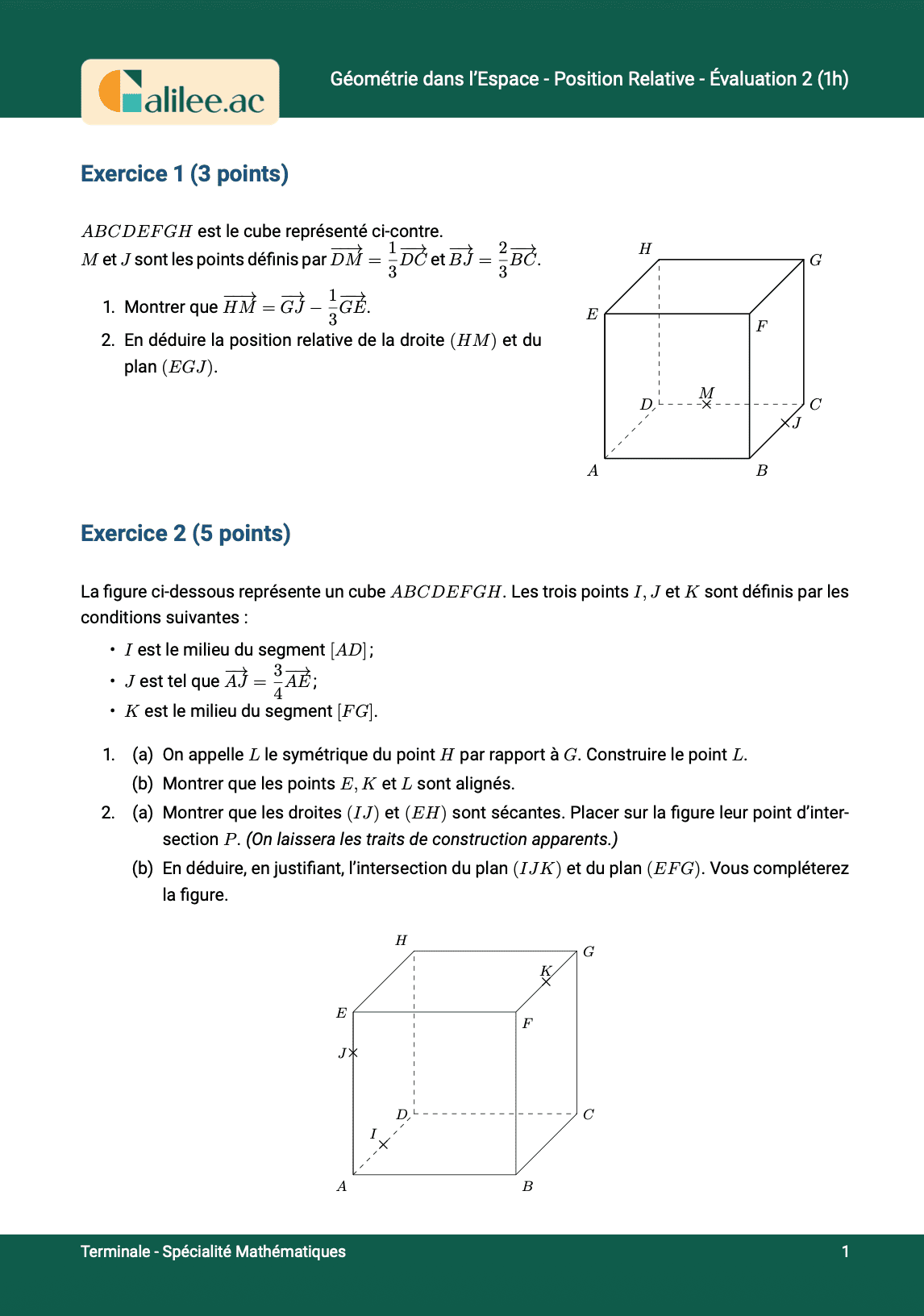
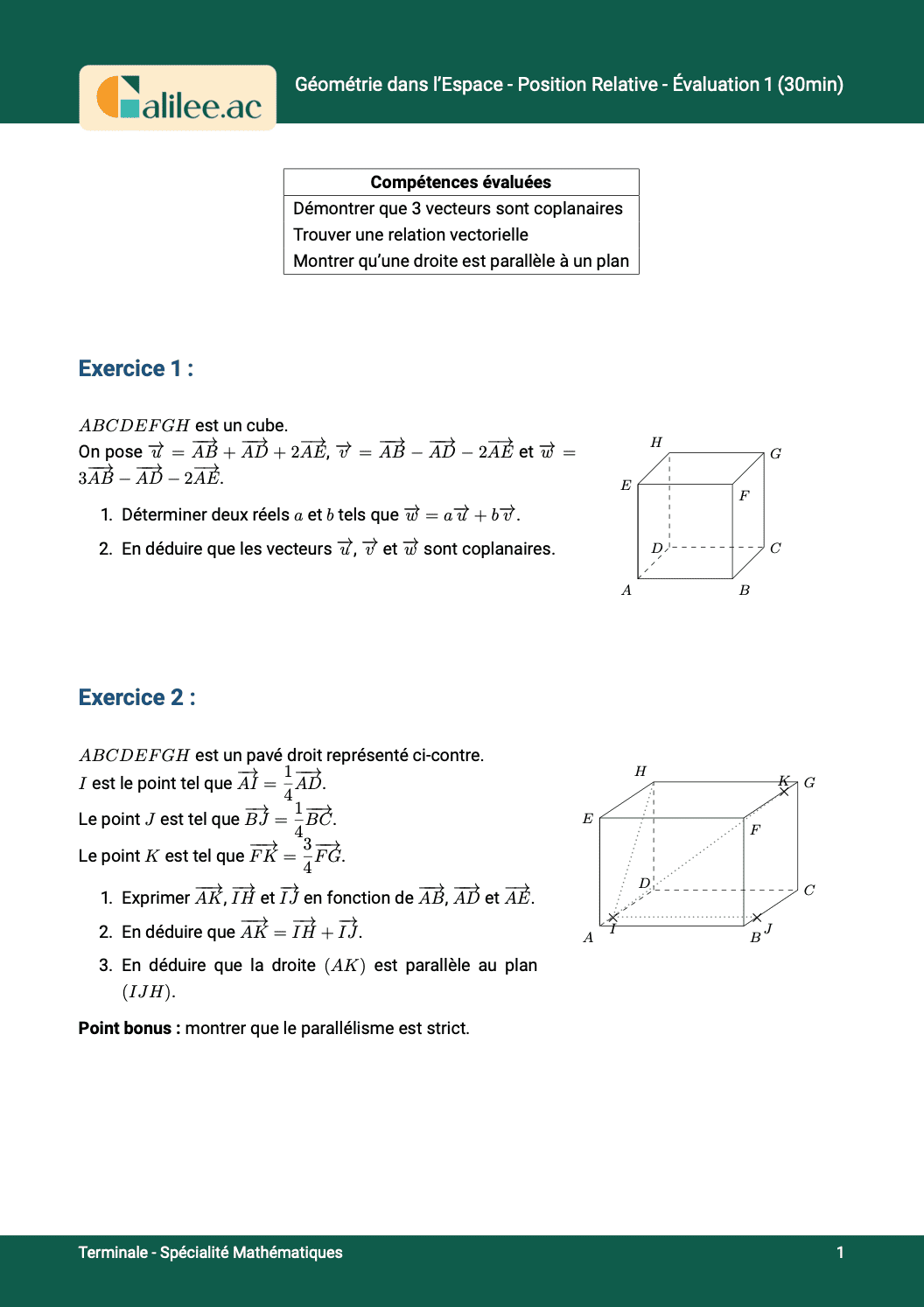
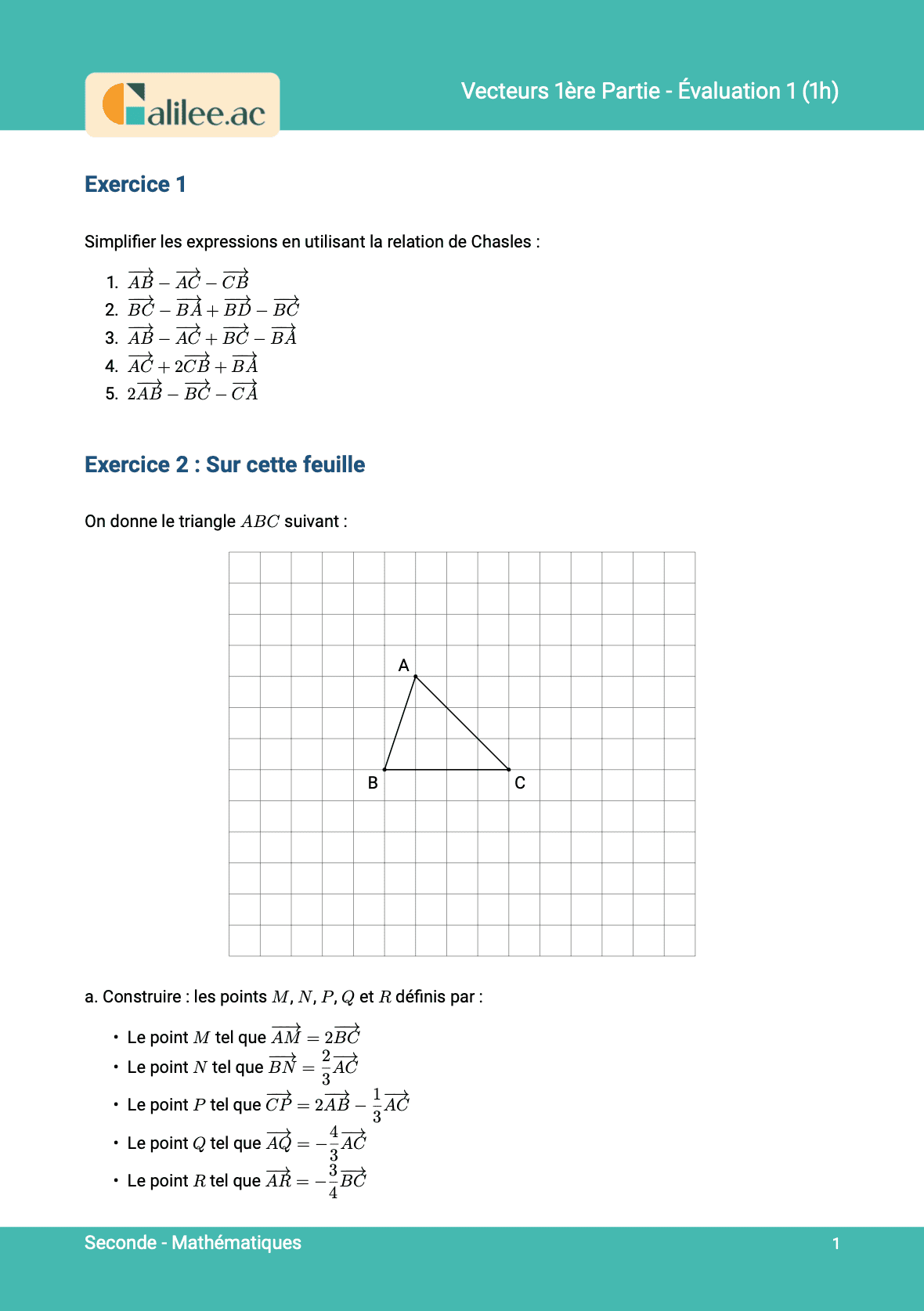
Livre
19. Coordonnées d'une somme, d'une différence, et d'un produit de vecteur
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Terminale spécialitéRecommandé
Contrôle Probabilités, Etudes de Fonctions et Suites, Géométrie dans l'Espace
Chapitres: Récurrence Étude de suites ...
SecondeRecommandé
Contrôle Vecteurs - 1ère Partie - 2
Chapitres: Vecteurs
SecondeRecommandé
Contrôle Vecteurs - 2ème Partie - 4
Chapitres: Vecteurs
SecondeRecommandé
Contrôle Vecteurs - 2ème Partie - 3
Chapitres: Vecteurs
Terminale spécialitéRecommandé
Contrôle Limites de Fonctions et Positions Relatives dans l'Espace
Chapitres: Vecteurs, droites et plans Représentations paramétriques et Équations cartésiennes ...
Terminale spécialitéRecommandé
Contrôle Etudes Suites, Fonctions, Dénombrement, Position Relative Espace
Chapitres: Étude de suites Dénombrement ...
SecondeRecommandé
Contrôle Vecteurs - 1ère Partie - 1
Chapitres: Vecteurs
Terminale spécialitéRecommandé
Contrôle Positions Relatives Géométrie Espace 1
Chapitres: Vecteurs, droites et plans
Terminale spécialitéRecommandé
Contrôle Positions Relatives Géométrie Espace 2
Chapitres: Vecteurs, droites et plans
bonjour, le problème exo 4.3 est toujours là ? je pense que vous avez oublié de corrigé ... ou pas, cordialement
Bonjour, je crois qu'il y a une erreur Exercice 4, Question 3:
2 x AB - 5 x AC c'est correct sauf qu'il y a une inversion au niveau du codage vous avez mis 2 x AB - 5 x CB.
C'est visible surtout sur la correction Exercice 4 question 3.
Maël
2 x AB - 5 x AC c'est correct sauf qu'il y a une inversion au niveau du codage vous avez mis 2 x AB - 5 x CB.
C'est visible surtout sur la correction Exercice 4 question 3.
Maël
Bonjour,
J'ai rencontré un petit problème à l'exercice 2 :
Au 3. quand il faut faire 3*vec(AB)-2*vec(AC)
La correction affiche le resultat de : 3*vec(AB)-2*vec(BC)
Cordielement
BRAVO Diego
J'ai rencontré un petit problème à l'exercice 2 :
Au 3. quand il faut faire 3*vec(AB)-2*vec(AC)
La correction affiche le resultat de : 3*vec(AB)-2*vec(BC)
Cordielement
BRAVO Diego
Bonjour @DiegoBravo
Le problème au niveau de l'exercice 3 a été résolu.
Peux-tu nous préciser le problème au niveau de l'exercice 2 ?
Merci le matheux !!
Le problème au niveau de l'exercice 3 a été résolu.
Peux-tu nous préciser le problème au niveau de l'exercice 2 ?
Merci le matheux !!
Je me suis trompé je voulais dire exercice 3 je pense 🙃
D'accord champion
Introduction
Allez les amis, on va très tranquillement regarder comment calculer les coordonnées d'une somme, d'une soustraction et d'une multiplication de vecteurs quand vous avez les coordonnées des vecteurs.Calcul des coordonnées d'une somme de vecteurs
Pour calculer les coordonnées d'une somme de vecteurs, ce n'est pas compliqué, vous faites la somme des coordonnées. Donc, si je calcule \(u + v\), je vais commencer par dire que la coordonnée en \(x\) est la somme des coordonnées en \(x\). Donc ça va être \(7 + 1 = 8\). Et la coordonnée en \(y\) est la somme des coordonnées en \(y\), donc \(5 - 1 = 4\). Donc mon vecteur \(u + v\) aura comme coordonnées \(8\) et \(4\).Calcul des coordonnées d'une soustraction de vecteurs
Si je veux faire \(u - v\), c'est exactement la même chose, sauf qu'au lieu de faire la somme des coordonnées de \(u\) et \(v\), je dois faire la différence des coordonnées de \(u\) et \(v\). Donc, \(u - v\) aura pour coordonnées \(7 - 1 = 6\) et \(5 - (-1)\), qui équivaut en fait à \(5 + 1 = 6\). Donc, les coordonnées de \(u - v\) seront \(6\) et \(6\).Calcul des coordonnées d'une multiplication de vecteurs
Si je veux faire \(u + 3v\), il faut d'abord que je commence par calculer les coordonnées de \(3v\). Pour avoir les coordonnées de \(3v\), je fais trois fois les coordonnées de \(v\). Avec \(v\) étant égal à \(1, -1\), \(3v\) vaudra \(3 \times 1 = 3\) et \(3 \times -1 = -3\). Et maintenant, je peux faire la somme des coordonnées de \(u\) et celle de \(3v\) en additionnant les valeurs, donc \(7 + 3 = 10\) et \(5 - 3 = 2\). Donc, le vecteur \(u + 3v\) aura pour coordonnées \(10\) et \(2\). Entraînez-vous, il y a des exercices qui sont donnés en dessous. C'est vraiment sans aucun effort, c'est du sudoku pour vous tous.Recrue
Visiteur anonyme
14 pts
