Livre
13. Démontrer une égalité de vecteurs avec Chasles
Conditions d'achèvement
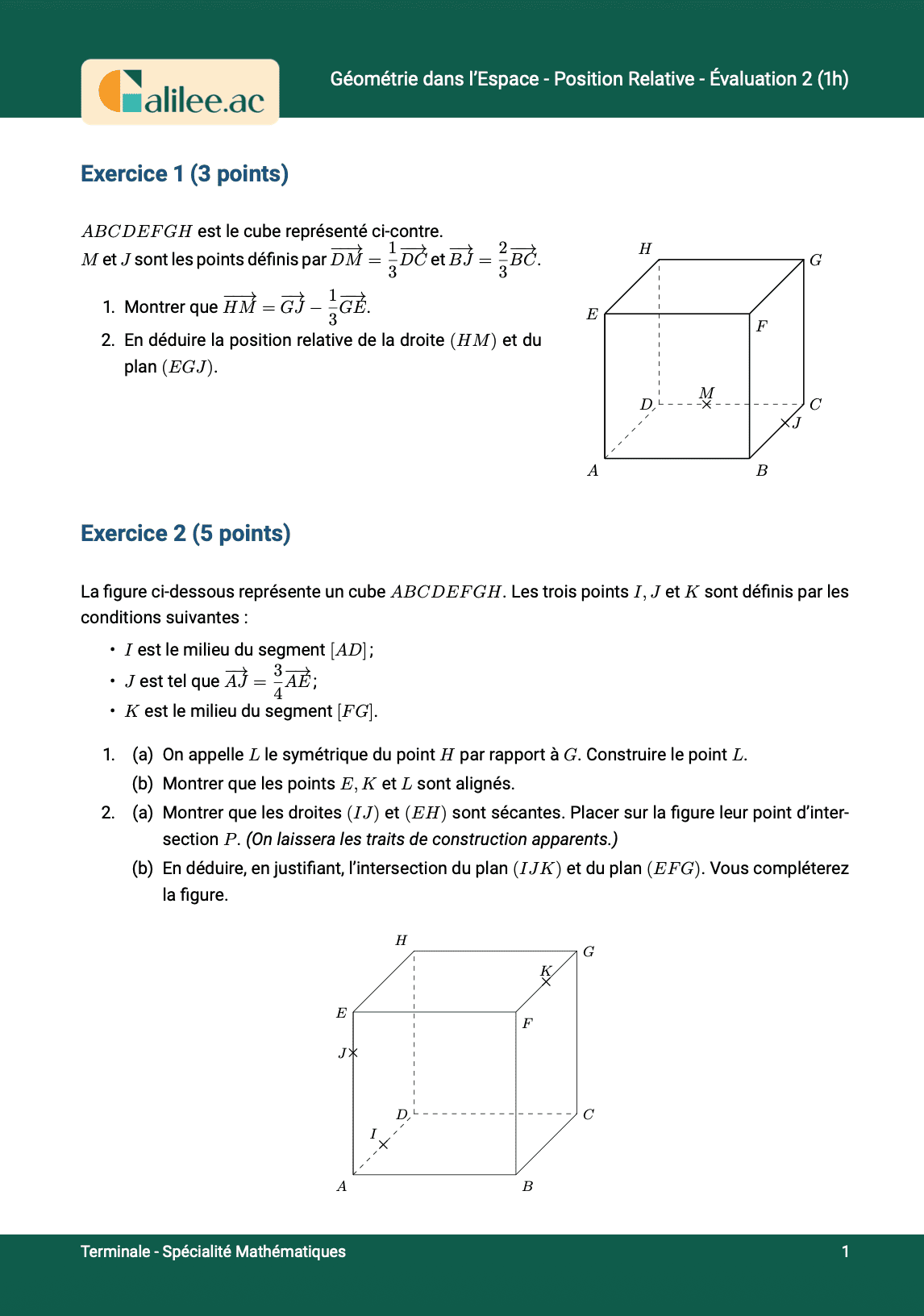
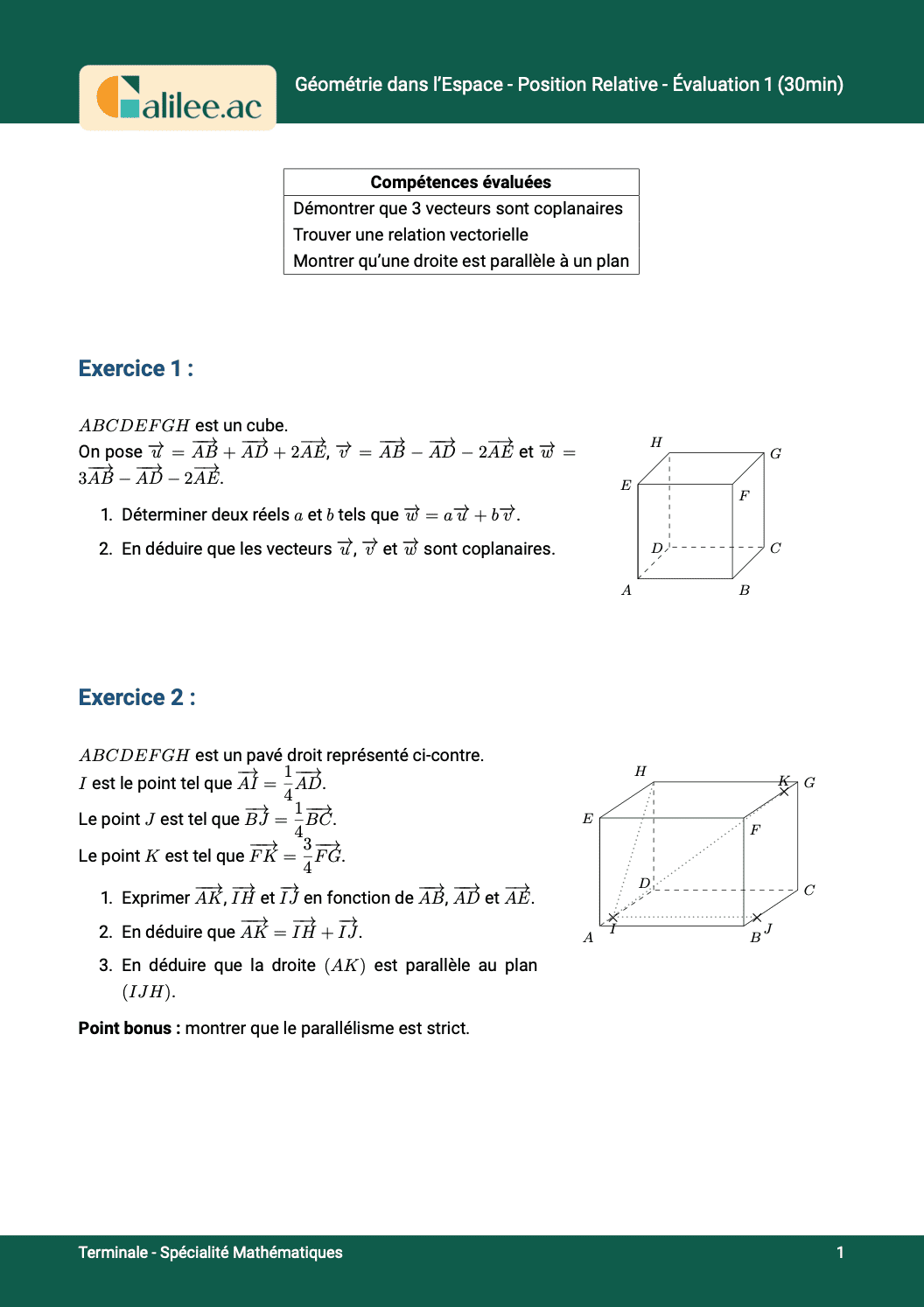
Exercice
1
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour utiliser la relation de Chasles pour montrer des égalités de vecteurs dans une figure. On a 6 vecteurs à considérer. La relation de Chasles nous permet de casser un vecteur en plusieurs petits vecteurs. Le problème c'est que souvent, quand on va casser notre vecteur, la somme de vecteurs qu'on va obtenir ne sera pas exactement celle qui est demandée. Du coup, il va falloir combiner la relation de Chasles avec des propriétés des figures, donc notamment les parallélogrammes, les côtés parallèles et les triangles équilatéraux qui ont tous les côtés d'une même longueur.Application de la relation de Chasles
On s'y met. On veut exprimer \(\overrightarrow{DA}\) en fonction de \(\overrightarrow{ED}\), \(\overrightarrow{DC}\) et \(\overrightarrow{DF}\). Je vous propose un moyen facile pour répondre à ces questions. Il va falloir que je trouve un chemin qui inclut trois vecteurs pour aller de D à A. Par exemple, j'ai supprimé le chemin \(\overrightarrow{DB} + \overrightarrow{BA}\) parce que celui-ci n'a que deux vecteurs. On va plutôt aller chercher un chemin avec trois vecteurs. Pour aller de D jusqu'à A, je vous propose de passer par C. On va faire \(\overrightarrow{DC} + \overrightarrow{CB} + \overrightarrow{BA}\). Je commence par dire que \(\overrightarrow{DA} = \overrightarrow{DC} + \overrightarrow{CB} + \overrightarrow{BA}\). Vous remarquerez que configurer une relation de Chasles a toujours la même structure. C'est toujours parce que la relation de Chasles vous permet de changer le point de passage.Combinaison de la relation de Chasles avec des propriétés des figures
Ensuite, on se dit qu'on veut \(\overrightarrow{CB}\), c'est cool, c'est bon, ça fait déjà un vecteur présent. Ensuite, \(\overrightarrow{DC}\), c'est donc ce vecteur là. Nous, on voudrait \(\overrightarrow{ED}\). C'est cool parce que \(\overrightarrow{DC}\) est égal à \(\overrightarrow{ED}\) vu que D est au milieu du vecteur \(\overrightarrow{DC}\). Donc je peux remplacer directement \(\overrightarrow{DC}\) par \(\overrightarrow{ED}\). On a donc \(\overrightarrow{DA} = \overrightarrow{ED} + \overrightarrow{CB} + \overrightarrow{BA}\). En regardant, vu que là et là on a deux triangles équilatéraux de même côté, forcément ce vecteur là est égal à ce vecteur là. Donc notre \(\overrightarrow{BA}\) c'est tout simplement \(\overrightarrow{DF}\). Et hop, j'ai démontré ma relation. J'encadre et je prends mes petits points. C'est pas grand chose mais quand même. Faites les exercices qui sont en dessous et ensuite vous allez voir comment on va combiner ça pour simplifier. Cette fois-ci, plutôt qu'expansion, on va réduire des relations de vecteurs. À vous de jouer.Nouvelle recrue
Visiteur anonyme
0 pts