Livre
11. Simplifier une somme de vecteurs avec un parallélogramme
Conditions d'achèvement
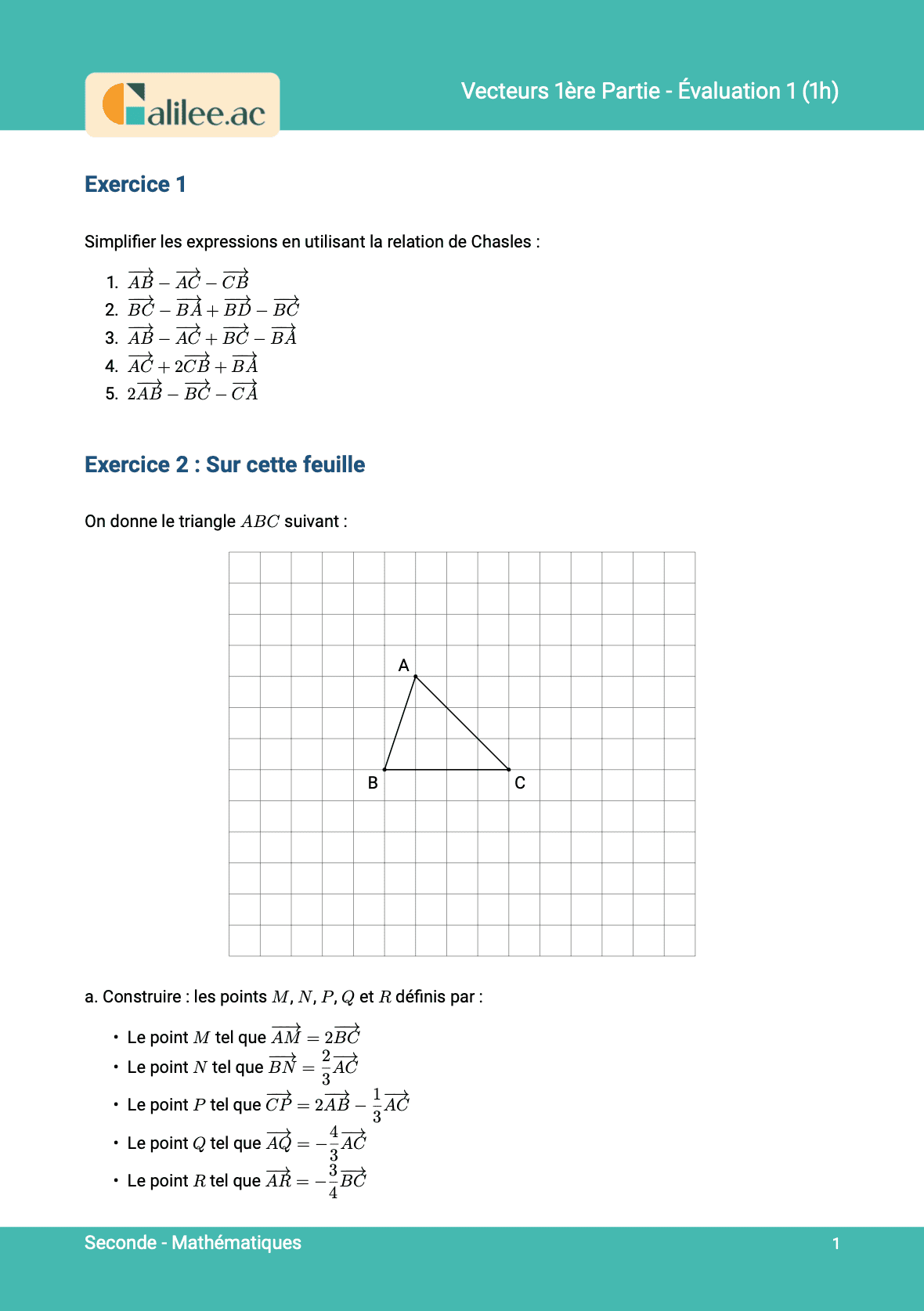
Exercice
1
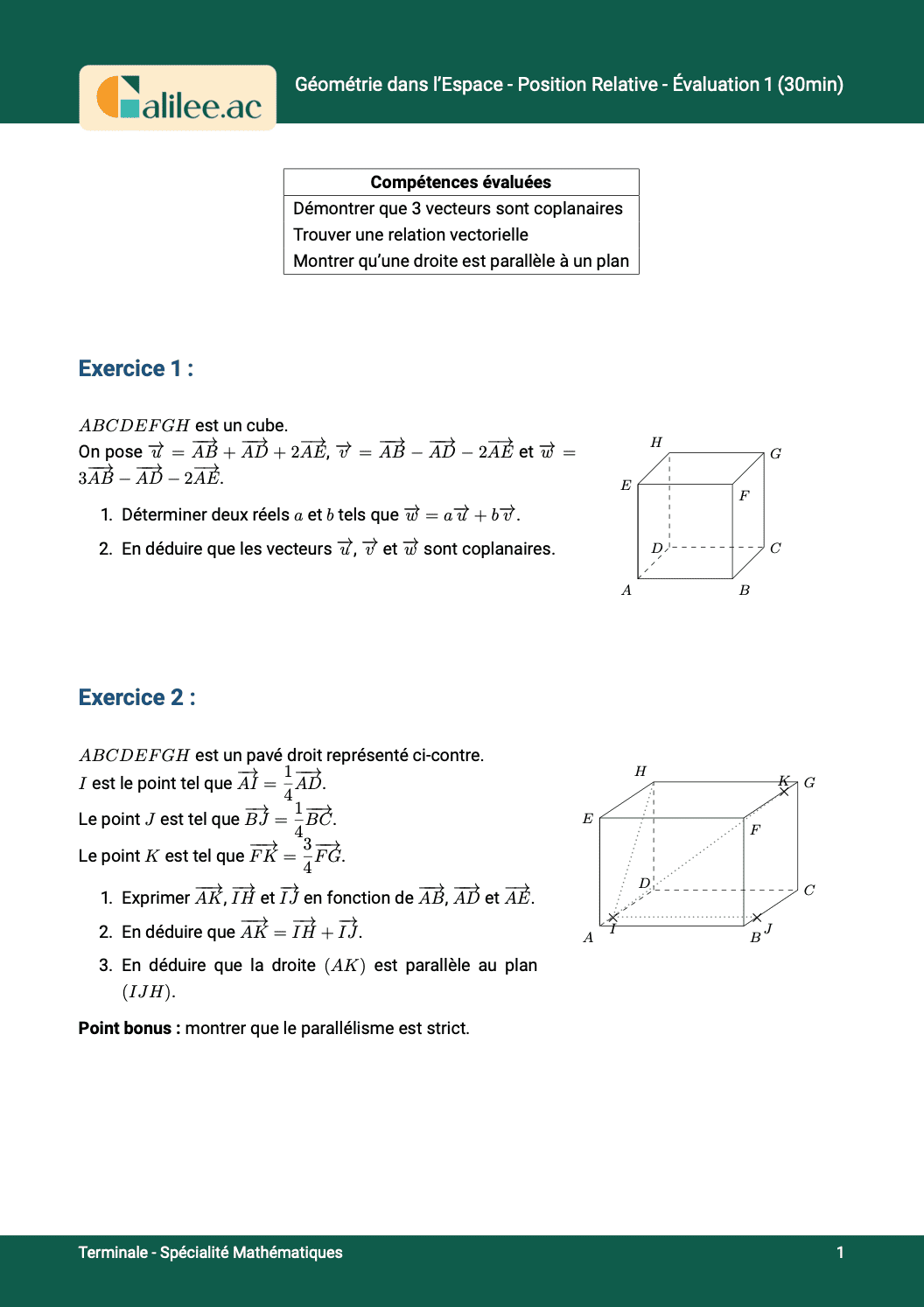
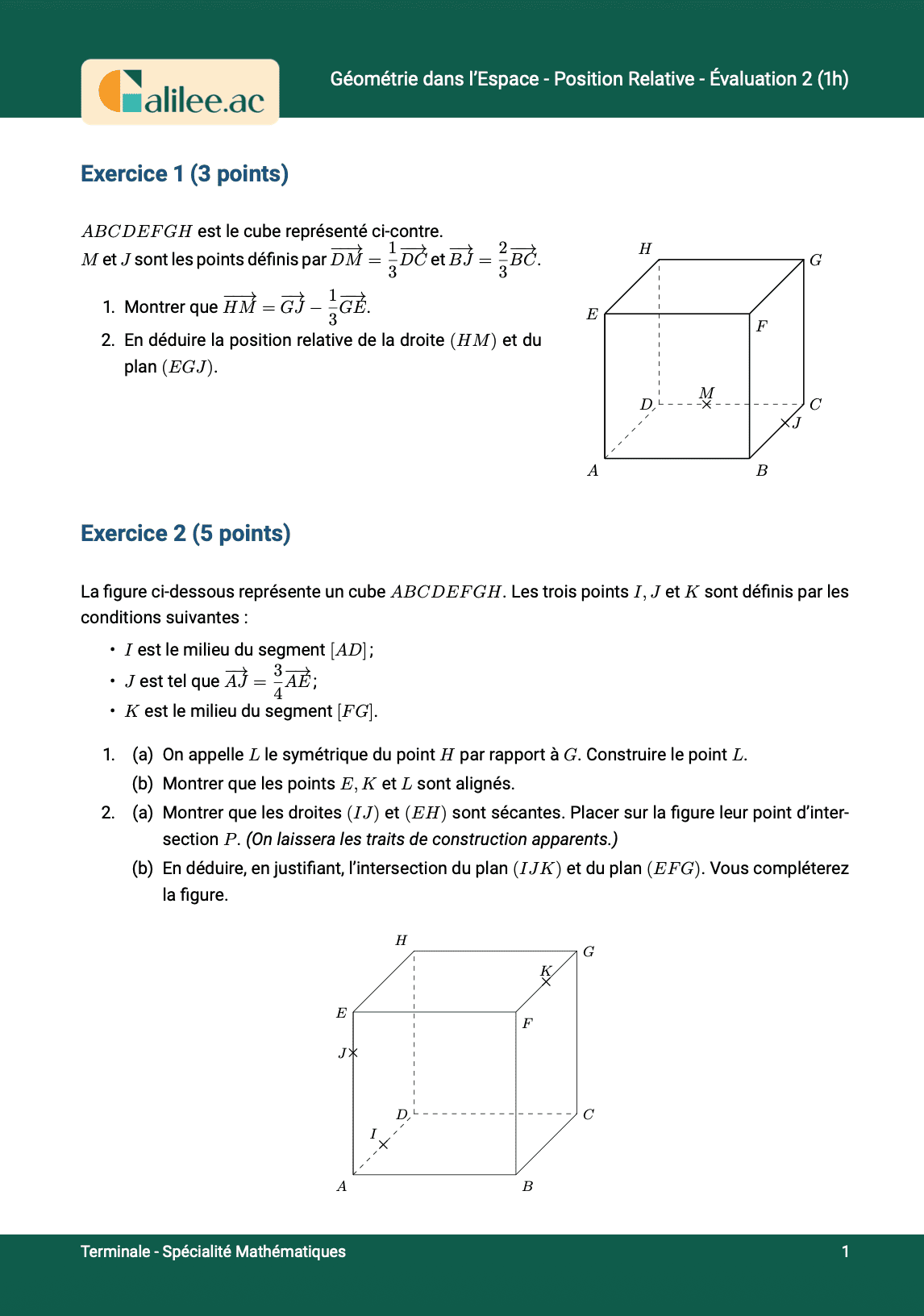
Exercice
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez, mettons-nous au travail. Dans cette vidéo, nous allons apprendre comment utiliser les propriétés du parallélogramme pour simplifier des équations vectorielles. Lorsque vous ferez un petit exercice que nous avons mis en dessous, vous verrez comment simplifier des égalités vectorielles compliquées, par exemple des sommes de vecteurs qui semblent ne ressembler à rien. Sachant que vous avez une figure et que vous savez que cette figure est un parallélogramme, en l'occurrence un carré, comment allez-vous vous y prendre ?Utilisation des propriétés du parallélogramme
Eh bien, nous allons utiliser la propriété du parallélogramme qui dit que le vecteur \(\vec{DE}\) est égal à \(\vec{AC}\). Nous allons également utiliser le fait que \(\vec{AC}\) est égal à \(\vec{BD}\) et nous allons utiliser cela pour exprimer la somme des vecteurs \(\vec{CA} - \vec{BA}\). Donc, je me dis que \(\vec{CA} - \vec{BA}\) est égal à \(\vec{AB}\). En effet, lorsque vous inversez l'ordre des lettres, vous obtenez le vecteur opposé. Donc, mon équation devient \(\vec{SA} + \vec{AB} + \frac{1}{2}\vec{BD} + \frac{1}{3}\vec{CB}\). Vous vous rendez compte que ces deux vecteurs, \(\vec{AC}\) et \(\vec{BD}\), sont égaux. Donc, nous allons pouvoir exprimer \(\vec{AC}\) en fonction de \(\vec{BD}\). C'est-à-dire, plutôt que de lire \(\vec{AC}\), je vais faire le choix de dire \(\vec{BD}\).Simplification de l'équation
Donc, je remplace \(\vec{AC}\) par \(\vec{BD}\) dans mon équation. Cela donne \(\vec{SA} + \vec{AB} + \frac{1}{2}\vec{BD} + \frac{1}{3}\vec{DB}\). Lorsque je fais la somme de \(\vec{CA}\) et \(\vec{AB}\), graphiquement, cela revient à partir de \(\vec{C}\) et arriver à \(\vec{D}\). En fait, \(\vec{CA} + \vec{AB} = \vec{CD}\). Maintenant, j'ai \(\frac{1}{2}\vec{BD} + \frac{1}{2}\vec{DB}\). Au même titre qu'on peut factoriser quand on écrit \(\frac{1}{2}x + \frac{1}{2}y = \frac{1}{2}(x + y)\), quand j'ai \(\frac{1}{2}\vec{BD} + \frac{1}{2}\vec{DB}\), j'ai \(\frac{1}{2}(\vec{BD} + \vec{DB})\). Je continue, \(\vec{DB}\) est l'opposé de \(\vec{BD}\), c'est-à-dire \(-\vec{BD}\). Donc, \(\vec{SA} + \vec{AB} + \frac{1}{2}\vec{BD} - \frac{1}{2}\vec{BD} = \vec{SA} + \vec{AB}\). En fin de compte, \(\vec{BD} - \vec{BD} = \vec{0}\).Conclusion
Voilà, j'ai utilisé les propriétés du parallélogramme, en l'occurrence un carré, pour simplifier fortement une équation de vecteurs. Nous avons mis des exercices en dessous pour vous entraîner. Vous allez voir que cela devient de plus en plus compliqué si vous maîtrisez cela. Le reste passera comme une lettre à la poste.Nouvelle recrue
Visiteur anonyme
0 pts