8. Antécédent f par le graphique

Introduction

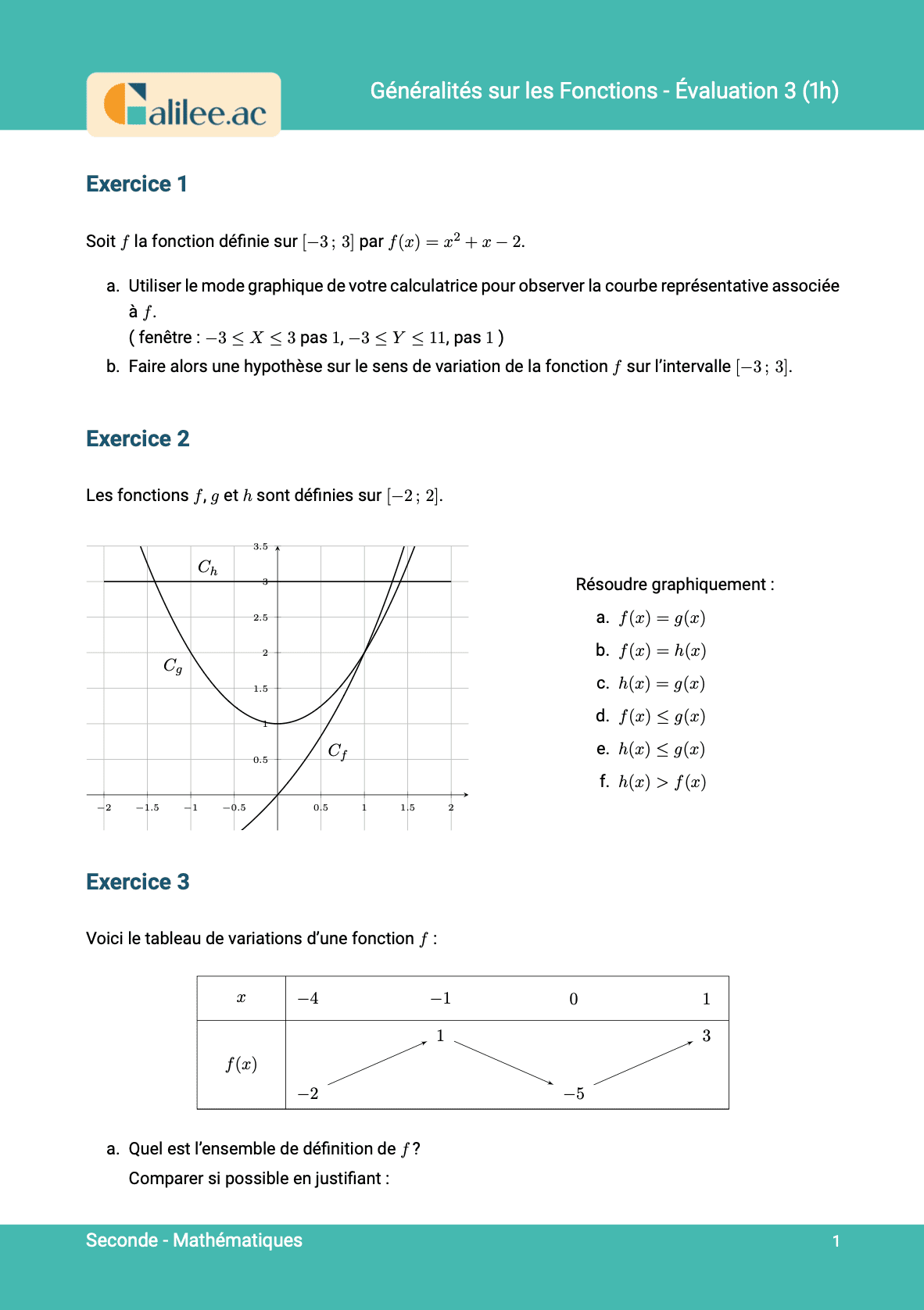
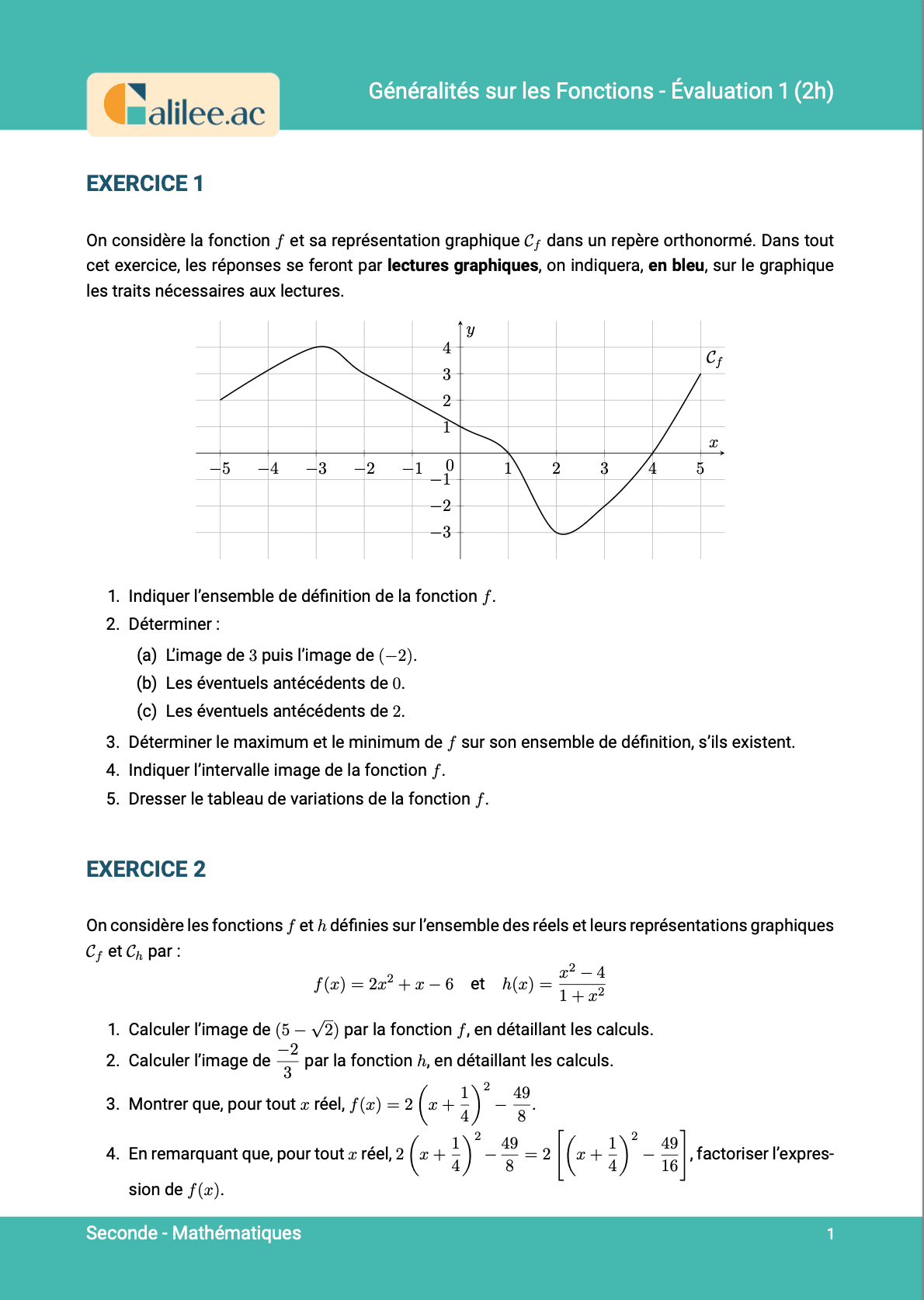
Cette fois-ci, on ne cherche plus les images par la fonction \(f\) avec la représentation graphique, on cherche les antécédents. Il faut faire attention, car on peut avoir plusieurs antécédents, on peut n'en avoir aucun, ou on peut en avoir plusieurs. C'est plusieurs cas possibles avec les fonctions. Avec les images, on en a qu'une seule maximum.

Comment trouver l'antécédent ?

C'est toujours la même réflexion qu'on s'est faite sur la vidéo d'avant. Comment fait-on pour trouver l'antécédent ? Tout à l'heure, on avait vu avec les images que quand on nous demande l'image, c'est forcément la fonction qu'on nous donne. C'était sur les abscisses parce que c'était l'antécédent. Si on cherche l'image, c'est parce qu'on nous a donné l'antécédent. Et si on cherche les antécédents, c'est qu'on nous a donné l'image. Le piège, encore une fois, est de se dire "antécédent, c'est les \(x\)", mais si on nous pose la question "quelle est l'antécédent ?", c'est forcément que l'information, c'est l'autre. C'est toujours ça le piège, c'est de s'inverser en images. Par exemple, si on nous demande les antécédents de 1,5, 1,5 c'est l'image, donc c'est sur les ordonnées.

Exemples

Prenons l'exemple où on nous demande l'antécédent de 1,5. On est obligé de descendre sur la courbe jusqu'à atteindre l'abscisse correspondante, qui est 0. Donc, l'antécédent de 1,5 par la fonction \(f\) est 0. Pour le cas de 0, on part de l'origine. Si on cherche les antécédents, on part des ordonnées pour aller aux abscisses. On coupe la courbe à deux endroits, donc on a deux antécédents : -2 et 1,5. Pour le cas de -1, on se place sur les ordonnées parce que -1 c'est une image. On coupe la courbe à deux endroits, donc on a deux antécédents : 2 et 3. Il faut bien se souvenir que pour les images, on aura toujours un maximum d'une image, mais pour les antécédents, on peut en avoir plusieurs ou pas. Par exemple, si on cherche les antécédents de 2 par la fonction \(f\), on se place à 2 sur les ordonnées, mais il n'y a pas d'image. C'est un cas qui peut arriver. Entraînez-vous à faire ça, faites plein de cas où on cherche l'image ou l'antécédent. Ça a l'air facile, mais il y a toujours moyen de se tromper, surtout avec ces histoires d'origine. Je pense que vous avez compris et on se dit à très bientôt. Salut.