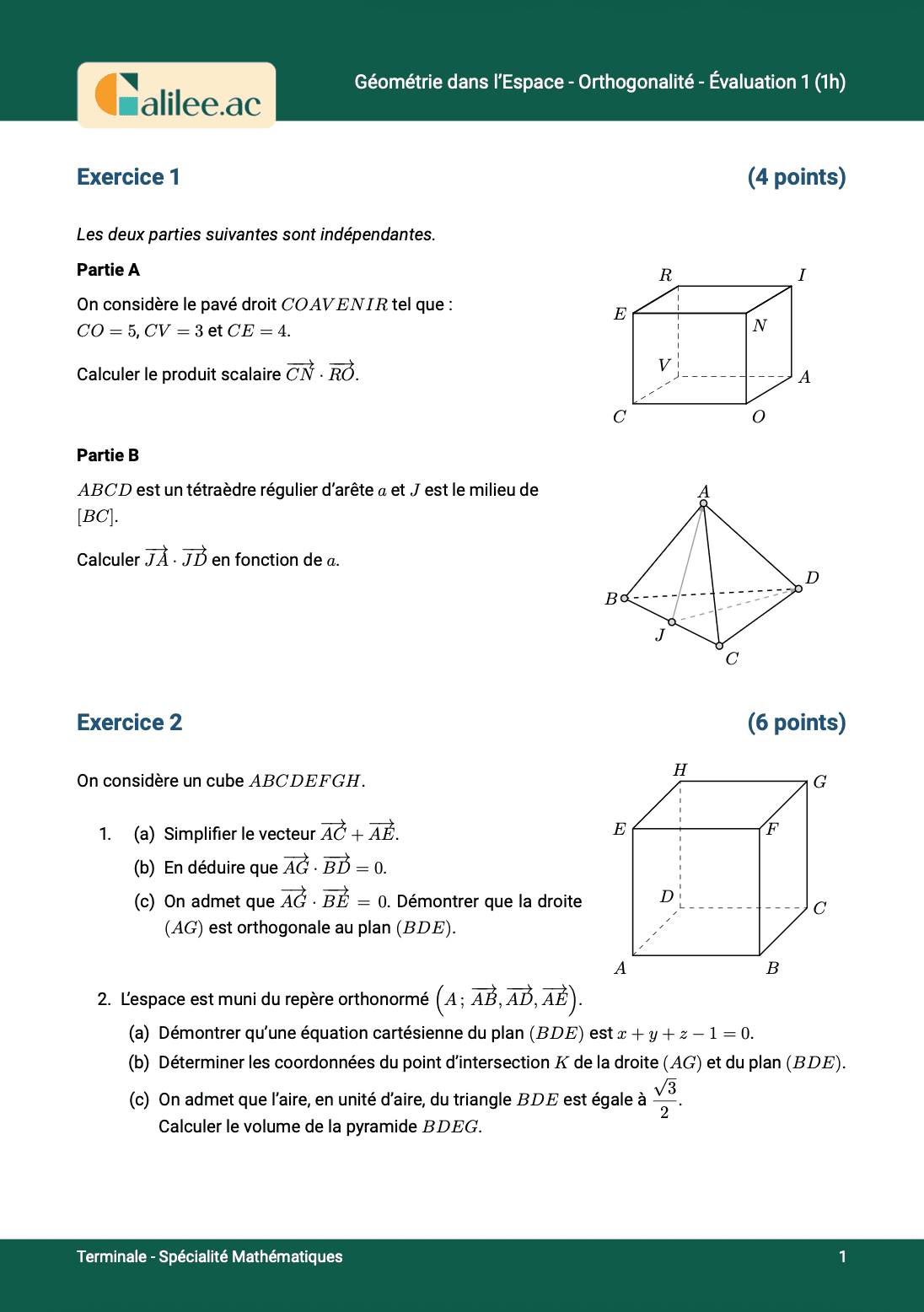
📖 Fiche résumée

Introduction au Produit Scalaire et à l'Orthogonalité dans l'Espace

Le chapitre sur le produit scalaire et l'orthogonalité dans l'espace est une pierre angulaire du programme de mathématiques de Terminale Spécialité. Il étend les concepts de la géométrie plane à un cadre tridimensionnel, offrant des outils puissants pour analyser les positions relatives des droites et des plans, calculer des angles et des distances. La maîtrise de ces notions est indispensable pour aborder sereinement les problèmes de géométrie dans l'espace, un thème récurrent au baccalauréat. Cette fiche de cours a pour objectif de synthétiser les définitions, formules et théorèmes essentiels pour vous aider à structurer vos révisions. Dans cet article, nous allons détailler chaque concept présenté dans notre fiche résumée, en expliquant les mécanismes et l'utilité de chaque formule. Nous aborderons les différentes manières de définir et de calculer le produit scalaire de deux vecteurs de l'espace, avant de nous plonger dans son application principale : la caractérisation de l'orthogonalité. Vous découvrirez comment utiliser le produit scalaire pour démontrer que des droites sont orthogonales, qu'une droite est orthogonale à un plan, ou que deux plans sont perpendiculaires. Bien que cet article soit exhaustif, il est conçu comme un complément à la fiche PDF disponible sur notre site, qui offre une présentation visuelle et condensée, idéale pour une mémorisation rapide avant les examens.

Le Produit Scalaire dans l'Espace : Définitions et Outils de Calcul

Le produit scalaire est une opération qui associe deux vecteurs et qui, contrairement à l'addition de vecteurs, ne résulte pas en un vecteur mais en un nombre réel (un scalaire). Cette opération possède des propriétés géométriques et algébriques très riches, ce qui en fait un outil de choix en physique (pour le calcul du travail d'une force, par exemple) et en mathématiques.

Les Deux Visages du Produit Scalaire : Définitions Fondamentales

Il existe deux manières principales de définir et de calculer le produit scalaire dans l'espace. Le choix de la méthode dépend des informations dont on dispose sur les vecteurs.

1. La Définition Géométrique : avec Norme et Angle

Cette définition met en lumière le lien direct entre le produit scalaire et la géométrie des vecteurs. Pour deux vecteurs non nuls u⃗ et v⃗ de l'espace, leur produit scalaire, noté u⃗ ⋅ v⃗, est donné par la formule :

u⃗ ⋅ v⃗ = ||u⃗|| × ||v⃗|| × cos(α)

Dans cette expression :

• ||u⃗|| et ||v⃗|| représentent respectivement les normes (ou longueurs) des vecteurs u⃗ et v⃗.
• α est la mesure de l'angle géométrique (non orienté) formé par les deux vecteurs, lorsque leurs origines coïncident.

Cette formule est particulièrement utile lorsque l'on connaît les longueurs des vecteurs et l'angle qui les sépare. Elle permet également de comprendre l'interprétation géométrique du produit scalaire : le signe du résultat dépend de l'angle α. Si l'angle est aigu (entre 0° et 90°), le cosinus est positif et le produit scalaire aussi. S'il est obtus (entre 90° et 180°), le cosinus est négatif, rendant le produit scalaire négatif. Le cas crucial, que nous développerons plus tard, est celui où l'angle est droit (90°), car le cosinus est alors nul, annulant le produit scalaire.

2. La Définition Analytique : avec les Coordonnées

En pratique, dans les exercices de géométrie dans un repère, on travaille le plus souvent avec les coordonnées des vecteurs. Dans un repère orthonormé (O; i⃗, j⃗, k⃗) de l'espace, si on a deux vecteurs u⃗(x, y, z) et v⃗(x', y', z'), leur produit scalaire est beaucoup plus simple à calculer :

u⃗ ⋅ v⃗ = xx' + yy' + zz'

Cette formule est le résultat de la distributivité du produit scalaire et des propriétés des vecteurs de la base (i⃗ ⋅ i⃗ = 1, i⃗ ⋅ j⃗ = 0, etc.). Elle transforme un problème de géométrie en un simple calcul algébrique. C'est la méthode à privilégier dès que l'on travaille dans un repère.

Autres Formules Utiles : Polarisation et Norme

Les Formules de Polarisation

Il existe des identités, appelées formules de polarisation, qui établissent un lien entre le produit scalaire et la norme des vecteurs. Elles sont particulièrement utiles dans des situations où les angles ne sont pas connus, mais où l'on peut calculer les longueurs de certaines sommes ou différences de vecteurs. Elles découlent directement du développement des carrés scalaires, en utilisant le fait que ||u⃗||² = u⃗ ⋅ u⃗.

• u⃗ ⋅ v⃗ = 1/2 ( ||u⃗ + v⃗||² - ||u⃗||² - ||v⃗||² )
• u⃗ ⋅ v⃗ = 1/2 ( ||u⃗||² + ||v⃗||² - ||u⃗ - v⃗||² )
• u⃗ ⋅ v⃗ = 1/4 ( ||u⃗ + v⃗||² - ||u⃗ - v⃗||² )

Ces formules, bien que moins fréquemment utilisées que la formule analytique, sont des outils puissants à garder en mémoire pour des configurations géométriques spécifiques.

Rappels sur le Calcul des Coordonnées et de la Norme

Pour utiliser efficacement les formules du produit scalaire, il est crucial de savoir déterminer rapidement les coordonnées d'un vecteur et sa norme.

• Coordonnées d'un vecteur : Pour deux points A(xₐ, yₐ, zₐ) et B(xₑ, yₑ, zₑ), le vecteur AB⃗ a pour coordonnées (xₑ - xₐ, yₑ - yₐ, zₑ - zₐ).
• Norme d'un vecteur : Pour un vecteur u⃗(x, y, z), sa norme est la longueur du segment qui le représente, calculée via une extension du théorème de Pythagore à l'espace : ||u⃗|| = √(x² + y² + z²).

L'Orthogonalité dans l'Espace : Application Majeure du Produit Scalaire

La véritable puissance du produit scalaire en géométrie dans l'espace réside dans sa capacité à détecter et à prouver l'orthogonalité. La condition est d'une simplicité remarquable et constitue le fondement de toutes les démonstrations de cette section.

Condition d'Orthogonalité de Deux Vecteurs

Le théorème central est le suivant :

Deux vecteurs u⃗ et v⃗ sont orthogonaux si et seulement si leur produit scalaire est nul : u⃗ ⋅ v⃗ = 0.

Cette équivalence est directe à partir de la définition géométrique. Si les vecteurs ne sont pas nuls, leur produit scalaire est nul si et seulement si cos(α) = 0, ce qui signifie que l'angle α est de 90° (π/2 radians). Cette propriété transforme un concept géométrique (l'angle droit) en une simple équation algébrique à vérifier.

Applications aux Droites et aux Plans

Armés de cette condition fondamentale, nous pouvons maintenant définir l'orthogonalité entre les objets de base de la géométrie spatiale : les droites et les plans.

1. Orthogonalité de deux droites

Soient deux droites (d₁) et (d₂) dirigées respectivement par les vecteurs directeurs u₁⃗ et u₂⃗. Les droites (d₁) et (d₂) sont dites orthogonales si leurs vecteurs directeurs sont orthogonaux. La condition est donc :

(d₁) ⊥ (d₂) ⇔ u₁⃗ ⋅ u₂⃗ = 0

Une note importante en géométrie spatiale : deux droites orthogonales ne sont pas nécessairement sécantes (perpendiculaires). Elles peuvent être non coplanaires tout en ayant des directions qui forment un angle droit.

2. Orthogonalité d'une droite et d'un plan

Une droite (d) est orthogonale à un plan (P) si elle est orthogonale à toutes les droites du plan (P). Heureusement, il n'est pas nécessaire de le vérifier pour toutes les droites. Un théorème puissant simplifie la tâche :

Une droite (d) de vecteur directeur u⃗ est orthogonale à un plan (P) si et seulement si u⃗ est orthogonal à deux vecteurs directeurs non colinéaires v₁⃗ et v₂⃗ du plan (P).

La condition de calcul est donc double :

• u⃗ ⋅ v₁⃗ = 0
• u⃗ ⋅ v₂⃗ = 0

Un vecteur comme u⃗, qui est orthogonal au plan, est appelé un vecteur normal au plan (P). La notion de vecteur normal est centrale pour définir l'équation cartésienne d'un plan.

Relations entre Droites et Plans : Parallélisme et Perpendicularité

Le concept d'orthogonalité permet également d'établir des relations de parallélisme et de perpendicularité entre les plans.

1. Parallélisme de deux plans

Une conséquence directe de la définition précédente est le théorème suivant :

Si deux plans (P₁) et (P₂) sont orthogonaux à une même droite (d), alors ces deux plans sont parallèles : (P₁) // (P₂).

Cela s'explique par le fait que les deux plans partagent la même direction normale, celle donnée par le vecteur directeur de la droite (d).

2. Perpendicularité de deux plans

L'angle entre deux plans est défini comme l'angle formé par leurs vecteurs normaux. Deux plans sont donc dits perpendiculaires si leurs vecteurs normaux sont orthogonaux.

Soient (P₁) et (P₂) deux plans, avec des vecteurs normaux respectifs n₁⃗ et n₂⃗. On a alors :

(P₁) ⊥ (P₂) ⇔ n₁⃗ ⋅ n₂⃗ = 0

Cette dernière propriété complète notre tour d'horizon des applications de l'orthogonalité dans l'espace. Elle montre comment le simple calcul d'un produit scalaire permet de déterminer la position relative de deux plans.

Conclusion : Une Notion Transversale et Essentielle

Le produit scalaire dans l'espace est bien plus qu'une simple formule de calcul. C'est le pont qui relie l'algèbre des coordonnées à la géométrie des angles et des positions. Sa principale application, la caractérisation de l'orthogonalité via l'équation u⃗ ⋅ v⃗ = 0, est un réflexe à acquérir absolument. Elle est la clé pour résoudre une grande variété de problèmes : trouver l'équation cartésienne d'un plan connaissant un point et un vecteur normal, projeter un point sur un plan, calculer la distance d'un point à une droite ou à un plan, etc. Cet article vous a fourni une base de connaissances détaillée pour comprendre en profondeur les concepts présentés dans notre fiche de cours. Pour une révision efficace, nous vous encourageons à télécharger la fiche PDF sur Galilee.ac. Sa structure synthétique et visuelle vous aidera à mémoriser les formules et les théorèmes clés, un atout précieux pour réussir vos évaluations et l'épreuve du baccalauréat.