📖 Fiche résumée
On t'offre cette fiche en cadeau de bienvenue !
Sache cependant que ces fiches sont normalement réservées aux utilisateurs premium, qui nous soutiennent financièrement et nous permettent de continuer à vous offrir une application de qualité ! ❤️
Si toi aussi tu veux nous soutenir, et accéder en illimité à nos contenus premium, n'hésite pas à voir nos offres !
— Balthazar et David de Galilee.ac
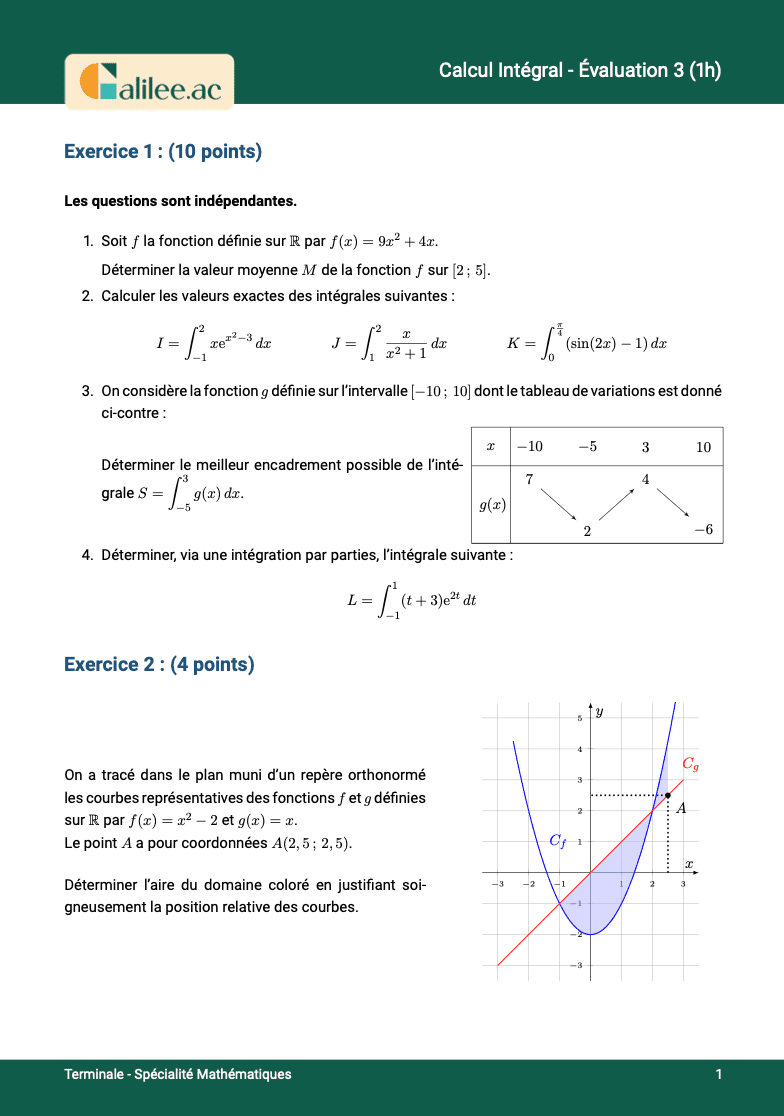
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction au Calcul Intégral en Terminale Spécialité
Le chapitre sur le calcul intégral est une pierre angulaire du programme de mathématiques en Terminale Spécialité. Il établit un lien fondamental entre deux concepts a priori distincts : la dérivation et le calcul d'aires. Cette fiche de cours a pour objectif de synthétiser les définitions, propriétés et techniques essentielles que tout élève doit maîtriser pour aborder sereinement les épreuves du baccalauréat. De la définition de l'intégrale d'une fonction continue à ses applications variées comme le calcul d'aires, l'intégration par parties ou la détermination de la valeur moyenne, ce résumé structuré vous guidera à travers les notions clés. Il est conçu pour être un support de révision complet, tout en vous encourageant à consulter la fiche PDF pour une vue d'ensemble schématique et visuelle des formules.
Définition de l'Intégrale d'une Fonction Continue
Le Théorème Fondamental de l'Analyse
Au cœur du calcul intégral se trouve une relation puissante qui le connecte à la dérivation. Soit f une fonction continue sur un intervalle [a, b]. On appelle primitive de f sur [a, b] toute fonction F dérivable sur cet intervalle telle que pour tout x ∈ [a, b], F'(x) = f(x).
L'intégrale de la fonction f entre les bornes a et b est alors définie par la formule suivante :
∫ (de a à b) f(x)dx = [F(x)] (entre a et b) = F(b) - F(a)
Cette expression, connue comme le théorème fondamental de l'analyse, est la clé de voûte de tous les calculs. Elle signifie que pour calculer l'intégrale d'une fonction, il suffit de trouver l'une de ses primitives (n'importe laquelle, car la constante d'intégration s'annule dans la soustraction F(b) - F(a)) et d'évaluer la différence de cette primitive aux bornes de l'intervalle. L'intégrale est donc un nombre réel qui dépend de la fonction f et de l'intervalle [a, b].
Les Propriétés Essentielles du Calcul Intégral
Pour manipuler les intégrales avec aisance, il est indispensable de connaître et de comprendre leurs propriétés algébriques. Celles-ci découlent directement de la définition et des propriétés de la dérivation.
La Linéarité de l'Intégrale
L'intégrale est un opérateur linéaire. Cela se traduit par deux règles principales :
- Homogénéité : Pour tout réel k, l'intégrale du produit d'une fonction par une constante est égale au produit de la constante par l'intégrale de la fonction. Formellement :
∫ (de a à b) k*f(x)dx = k * ∫ (de a à b) f(x)dx. Cette propriété permet de "sortir" les constantes multiplicatives de l'intégrale pour simplifier le calcul. - Additivité : L'intégrale d'une somme de fonctions est la somme de leurs intégrales :
∫ (de a à b) [f(x) + g(x)]dx = ∫ (de a à b) f(x)dx + ∫ (de a à b) g(x)dx. Cette règle est cruciale pour décomposer des fonctions complexes en termes plus simples à intégrer.
La Relation de Chasles
Cette propriété, analogue à celle des vecteurs, permet de décomposer une intégrale sur un intervalle en une somme d'intégrales sur des sous-intervalles. Pour tout point c appartenant à l'intervalle [a, b] (ou même en dehors), on a :
∫ (de a à c) f(x)dx = ∫ (de a à b) f(x)dx + ∫ (de b à c) f(x)dx
Géométriquement, si f est positive, cela signifie que l'aire sous la courbe de a à c est la somme de l'aire de a à b et de celle de b à c. Cette relation est particulièrement utile pour les fonctions définies par morceaux ou pour calculer des aires lorsque la fonction change de signe.
Propriétés liées aux Bornes d'Intégration
Deux conventions importantes sont à retenir :
- Inversion des bornes : Inverser les bornes d'une intégrale change son signe.
∫ (de a à b) f(x)dx = - ∫ (de b à a) f(x)dx. - Bornes égales : L'intégrale sur un intervalle de longueur nulle est nulle :
∫ (de a à a) f(x)dx = F(a) - F(a) = 0.
Positivité et Comparaison d'Intégrales (Croissance de l'Intégrale)
Cette propriété établit un lien entre l'ordre des fonctions et l'ordre de leurs intégrales.
- Positivité : Si une fonction f est positive sur l'intervalle [a, b] (avec a ≤ b), alors son intégrale sur cet intervalle est également positive :
Si f(x) ≥ 0, alors ∫ (de a à b) f(x)dx ≥ 0. - Comparaison : Si une fonction f est inférieure ou égale à une fonction g sur [a, b] (avec a ≤ b), alors l'intégrale de f est inférieure ou égale à l'intégrale de g :
Si f(x) ≤ g(x), alors ∫ (de a à b) f(x)dx ≤ ∫ (de a à b) g(x)dx.
Cette dernière propriété est fondamentale pour encadrer la valeur d'une intégrale qu'on ne saurait pas calculer directement.
Application Géométrique Majeure : Le Calcul d'Aires
L'interprétation la plus intuitive de l'intégrale est le calcul de l'aire d'une surface délimitée par des courbes. L'unité de mesure de cette aire est appelée unité d'aire (u.a.), qui correspond à l'aire d'un rectangle de côtés 1 unité sur l'axe des abscisses et 1 unité sur l'axe des ordonnées.
Cas d'une Fonction Continue et Positive
Si f est une fonction continue et positive sur [a, b], alors l'intégrale ∫ (de a à b) f(x)dx correspond exactement à l'aire, en u.a., du domaine 𝓐 délimité par la courbe représentative de f (𝓒f), l'axe des abscisses, et les droites verticales d'équations x = a et x = b.
Cas d'une Fonction Continue et Négative
Si f est une fonction continue et négative sur [a, b], l'intégrale ∫ (de a à b) f(x)dx sera un nombre négatif. L'aire 𝓐 du domaine, qui est par définition une quantité positive, est alors égale à l'opposé de l'intégrale :
𝓐 = - ∫ (de a à b) f(x)dx
Cas d'une Fonction changeant de Signe
Lorsque la fonction f change de signe sur l'intervalle [a, b], il est nécessaire de décomposer le calcul. La méthode est la suivante :
- Étudier le signe de f(x) sur [a, b] pour identifier les sous-intervalles où la fonction est positive et ceux où elle est négative.
- Utiliser la relation de Chasles pour découper l'intégrale aux points où la courbe coupe l'axe des abscisses.
- Calculer l'aire sur chaque sous-intervalle en prenant la valeur absolue de l'intégrale (c'est-à-dire l'intégrale si f est positive, et son opposé si f est négative).
- Additionner toutes les aires ainsi obtenues.
Par exemple, si f est positive sur [a, c] et négative sur [c, b], l'aire totale est : 𝓐 = ∫ (de a à c) f(x)dx - ∫ (de c à b) f(x)dx.
Une Technique de Calcul Avancée : l'Intégration par Parties (IPP)
Certaines fonctions, notamment les produits de fonctions (comme x*e^x ou x*ln(x)), n'ont pas de primitive évidente. L'intégration par parties est une technique puissante, issue de la formule de dérivation d'un produit, qui permet de transformer une intégrale difficile en une autre, espérons-le, plus simple.
Soient u et v deux fonctions dérivables sur [a, b]. La formule de l'IPP est :
∫ (de a à b) u'(x)v(x)dx = [u(x)v(x)] (entre a et b) - ∫ (de a à b) u(x)v'(x)dx
Le succès de cette méthode repose sur un choix judicieux des fonctions u' et v. L'objectif est de choisir v(x) de telle sorte que sa dérivée v'(x) soit plus simple, et u'(x) de manière à ce que sa primitive u(x) soit facile à calculer. Une astuce consiste à choisir pour v(x) la fonction qui se simplifie par dérivation (logarithme, polynôme), et pour u'(x) une fonction facile à intégrer (exponentielle, sinus, cosinus).
La Valeur Moyenne d'une Fonction
L'intégrale permet également de définir la notion de valeur moyenne d'une fonction continue sur un segment, ce qui a de nombreuses applications en physique, économie ou statistiques.
Définition et Formule
La valeur moyenne d'une fonction f continue sur un intervalle [a, b] (avec a ≠ b) est le nombre réel μ (mu) défini par :
μ = (1 / (b - a)) * ∫ (de a à b) f(x)dx
Interprétation Géométrique
Géométriquement, la valeur moyenne μ est la hauteur du rectangle de base (b - a) qui aurait la même aire que l'aire sous la courbe de f sur l'intervalle [a, b]. En d'autres termes, l'aire du rectangle μ * (b - a) est égale à l'aire ∫ (de a à b) f(x)dx. Cela revient à "aplanir" la courbe de f pour obtenir une fonction constante ayant la même aire sur le même intervalle.
Conclusion : Une Notion Centrale à Maîtriser
Le calcul intégral est un chapitre dense mais extrêmement cohérent. Sa maîtrise passe par une compréhension profonde du lien entre primitive et intégrale, une connaissance parfaite des propriétés opératoires, et une capacité à identifier la bonne méthode (calcul direct, IPP, décomposition) face à un problème. Savoir interpréter géométriquement l'intégrale en termes d'aire est indispensable pour résoudre une grande partie des exercices du baccalauréat. Ce texte vous a fourni une explication détaillée de tous les concepts présents dans la fiche de cours. Pour une mémorisation efficace des formules et des schémas clés, nous vous recommandons vivement de consulter la fiche PDF synthétique qui accompagne ce résumé. Elle vous offrira un aperçu visuel et concis, idéal pour vos dernières révisions.