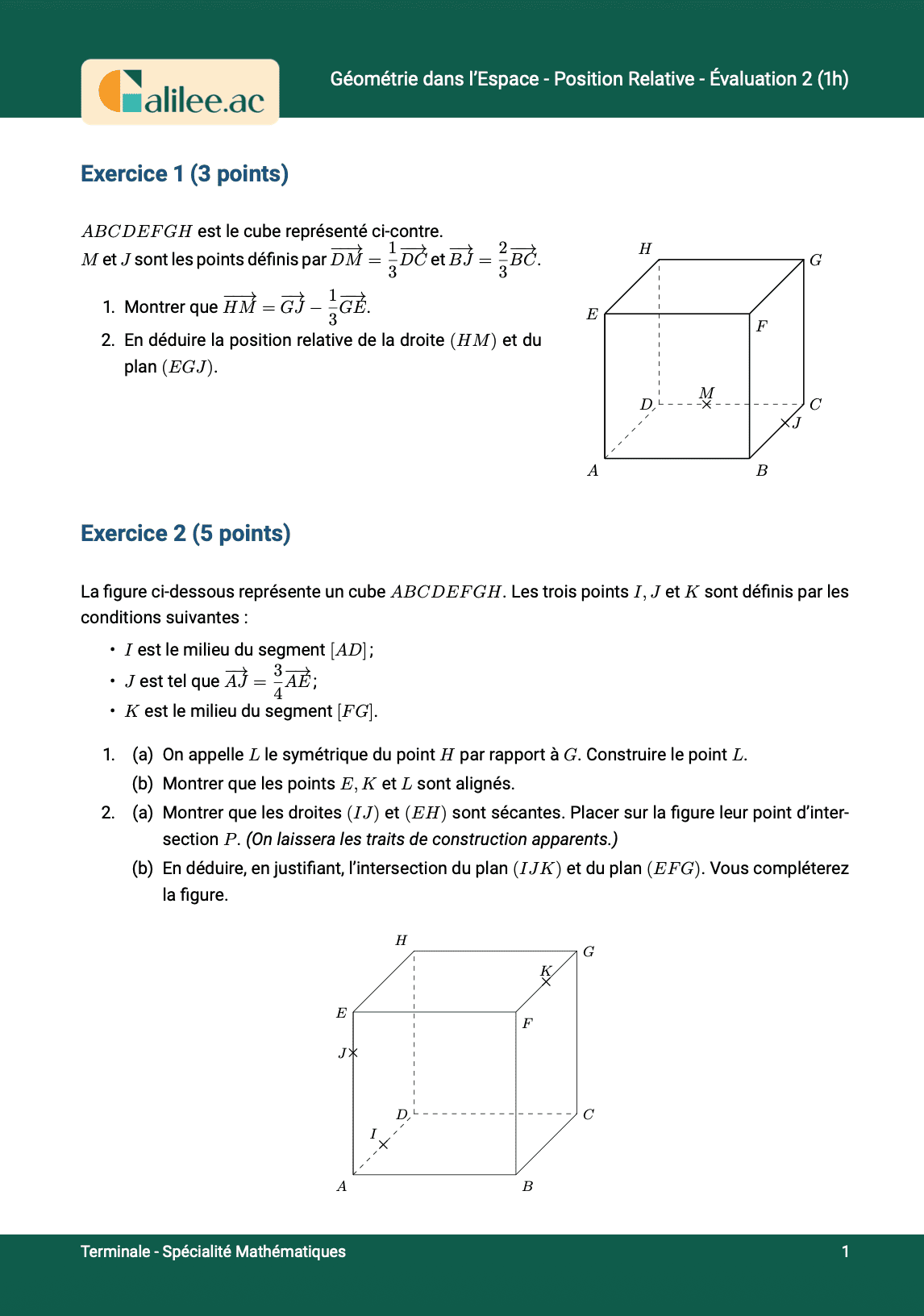
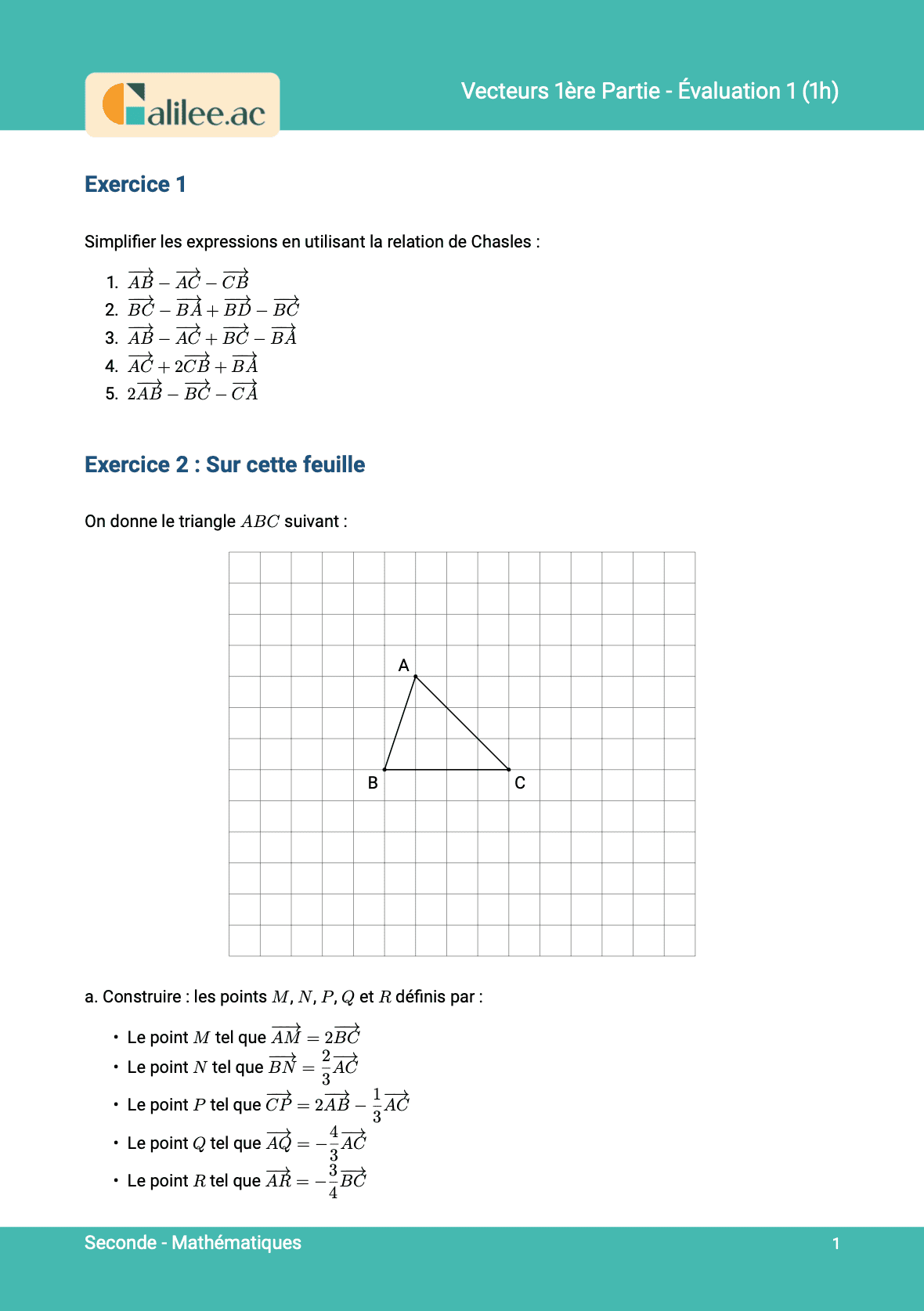
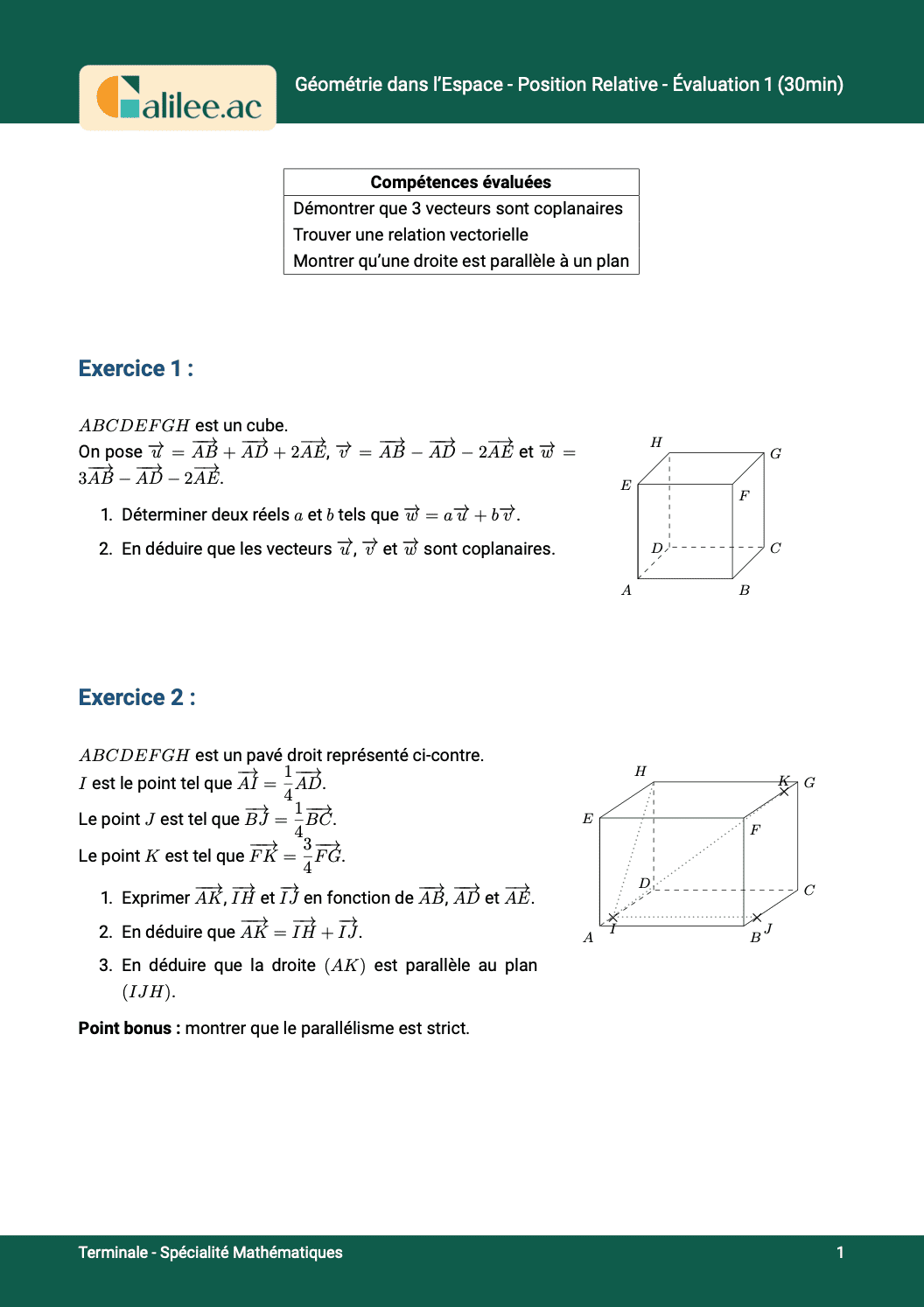
Livre
9. Egalités de vecteurs dans un parallélogramme
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Terminale spécialitéRecommandé
Contrôle Etudes Suites, Fonctions, Dénombrement, Position Relative Espace
Chapitres: Étude de suites Dénombrement ...
Terminale spécialitéRecommandé
Contrôle Positions Relatives Géométrie Espace 2
Chapitres: Vecteurs, droites et plans
Terminale spécialitéRecommandé
Contrôle Positions Relatives Géométrie Espace 1
Chapitres: Vecteurs, droites et plans
SecondeRecommandé
Contrôle Vecteurs - 1ère Partie - 2
Chapitres: Vecteurs
SecondeRecommandé
Contrôle Vecteurs - 1ère Partie - 1
Chapitres: Vecteurs
Terminale spécialitéRecommandé
Contrôle Probabilités, Etudes de Fonctions et Suites, Géométrie dans l'Espace
Chapitres: Récurrence Étude de suites ...
SecondeRecommandé
Contrôle Vecteurs - 2ème Partie - 3
Chapitres: Vecteurs
SecondeRecommandé
Contrôle Vecteurs - 2ème Partie - 4
Chapitres: Vecteurs
Terminale spécialitéRecommandé
Contrôle Limites de Fonctions et Positions Relatives dans l'Espace
Chapitres: Vecteurs, droites et plans Représentations paramétriques et Équations cartésiennes ...
Merci pour vos vidéos et exercices qui nous sont d'une grandes aides. Cependant, j'aimerai savoir, si il est possible de poser des questions.
Oui, dans l'espae commentaire !
Bof surtout les truc payant j aurais préféré avoir full pub que attendre 1H
Bonjour @titilacitrouilletitilacitrouille
Nous préférons que nos élèves révises sans être déranger par les publicités !!
Si cela te demande d'attendre 1H c'est à cause des erreurs et 1h est le timing pour revoir le cours et refaire les exercices où tu as eu les erreurs.
Merci pour la compréhension
Nous préférons que nos élèves révises sans être déranger par les publicités !!
Si cela te demande d'attendre 1H c'est à cause des erreurs et 1h est le timing pour revoir le cours et refaire les exercices où tu as eu les erreurs.
Merci pour la compréhension
Bien le bonjour,
J'ai rencontré un problème au cours de l'exercice 1, la réponse correcte rentrée
(ici vec(AD)=vec(BC)=vec(FE))
Pourtant le site me renvoie que j'ai une mauvaise réponse en m'indiquant la correction :
Correction : vec(AD)=vec(BC)=vec(FE)
Je ne comprends pas
Cordialement
BRAVO Diego
[Image pour illustrer](https://drive.google.com/file/d/1WdQWp65K8Y7VSTc3EbDBogEWK7_nmEoI/view?usp=sharing)
J'ai rencontré un problème au cours de l'exercice 1, la réponse correcte rentrée
(ici vec(AD)=vec(BC)=vec(FE))
Pourtant le site me renvoie que j'ai une mauvaise réponse en m'indiquant la correction :
Correction : vec(AD)=vec(BC)=vec(FE)
Je ne comprends pas
Cordialement
BRAVO Diego
[Image pour illustrer](https://drive.google.com/file/d/1WdQWp65K8Y7VSTc3EbDBogEWK7_nmEoI/view?usp=sharing)
Content de te voir ici Diego, le prof arrive ;)
Bonjour champion.
Le problème est résolu tu peux réessayer.
Merci Diego
Le problème est résolu tu peux réessayer.
Merci Diego
Introduction
Allez les amis, on est parti pour voir une propriété fondamentale du cours sur les vecteurs : les relations entre les vecteurs et les parallélogrammes. On va voir ça tout de suite.Qu'est-ce qu'un parallélogramme ?
Il faut que vous compreniez d'abord ce qu'est un parallélogramme. Un parallélogramme est un quadrilatère, c'est-à-dire un objet avec quatre côtés, dont les côtés opposés sont parallèles. Donc, un carré, un rectangle sont des exemples de parallélogrammes. Par exemple, dans un rectangle, ce côté-là et ce côté-là sont parallèles, et ce côté-là et ce côté-là sont parallèles. Cet objet, le BCEF, est un parallélogramme aussi, et pourtant ce n'est pas un rectangle. Donc, un parallélogramme peut être un rectangle, ou bien un objet dont les côtés peuvent être étirés ou déformés tout en restant parallèles.Propriété fondamentale des parallélogrammes
La propriété fondamentale des parallélogrammes, c'est que dans un parallélogramme, les côtés opposés forment des vecteurs égaux. Autrement dit, le vecteur \( \overrightarrow{DA} \) est exactement le même que le vecteur \( \overrightarrow{CB} \), et de la même manière, le vecteur \( \overrightarrow{BC} \) est le même que le vecteur \( \overrightarrow{EF} \). Une fois que vous avez compris ça, vous avez quasiment fini l'exercice. Pourquoi ? Parce que si \( ABCD \) est un rectangle, donc un parallélogramme, alors \( \overrightarrow{AB} = \overrightarrow{DC} \). Mais comme \( DC = EF \) (car \( BCEF \) est aussi un parallélogramme), alors \( \overrightarrow{AB} = \overrightarrow{EF} \). De plus, \( \overrightarrow{BC} = \overrightarrow{EF} \) aussi, car \( BCEF \) est un parallélogramme. Donc, si \( \overrightarrow{AB} = \overrightarrow{EF} \) et \( \overrightarrow{BC} = \overrightarrow{EF} \), alors \( \overrightarrow{AB} = \overrightarrow{BC} \). La démonstration est terminée. C'est un cas simple, mais dans les exercices, on a mis des cas simples et des cas plus compliqués. Entraînez-vous, car cela vaut littéralement deux ou trois points aux contrôles que vous allez avoir dans quelques semaines. Donc, ça vaut le coup de se dire : "Je me fais un ou deux exercices pour vérifier que c'est bien compris". À vous de jouer maintenant.Nouvelle recrue
Visiteur anonyme
2 pts
