Livre
8. Taux d'évolution réciproques
Conditions d'achèvement
Exercice
1
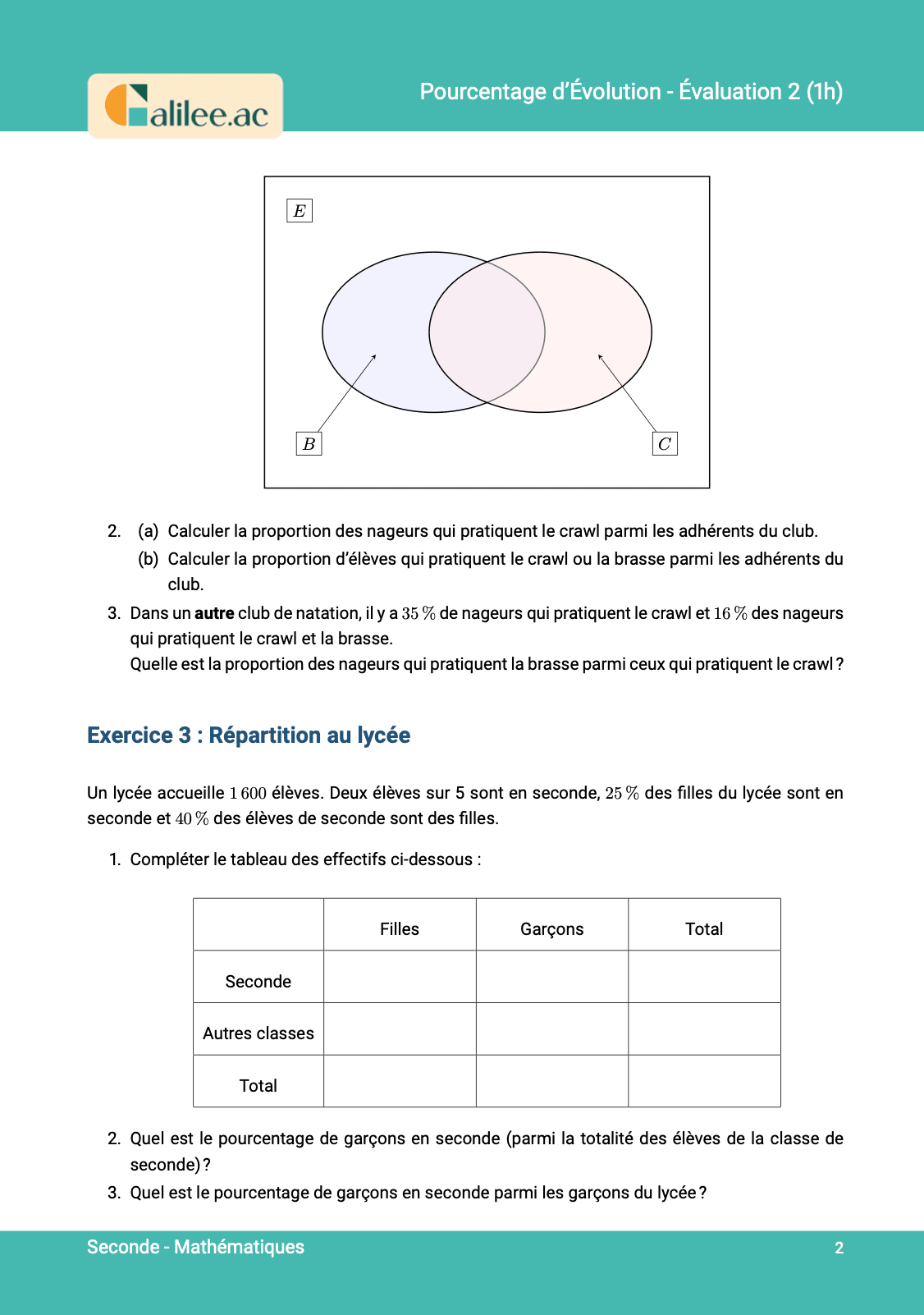
Exercice
2
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les amis, on est parti pour voir le truc le plus chaud qui a sur les taux d'évolution : c'est le taux d'évolution réciproque. On s'y met tous. On vous donne un article qui est soldé à 20%. Donc, j'ai un prix initial, je vais arriver à un prix final et là, j'aurais enlevé 20%. Le taux d'évolution réciproque, c'est le taux qui va permettre de passer du nouveau prix vers l'ancien prix.Comprendre le taux d'évolution réciproque
On a un réflexe qui est de dire que si j'ai diminué le prix de 20% pour retrouver mon prix initial, je vais faire plus 20%. Surtout pas ! C'est d'ailleurs l'exercice du banquet qu'on va faire après. Le taux d'évolution réciproque, il n'est pas égal au taux d'évolution dans le sens normal. Pourquoi ? Parce que si vous avez une réduction de 20%, vous allez enlever 20 euros sur un pull à 100 euros, donc vous allez vous retrouver à 80 euros. Si maintenant vous augmentez à nouveau de 20%, ces 80 euros, ce 20% ne va plus être calculé sur 100 euros comme dans le volet, mais sur 80 euros. Donc cette augmentation de 20% ne sera pas exactement pareil. Du coup, si je fais moins 20% puis que je rajoute 20%, je ne passe pas de 80 à 100 mais de 80 à 96. Donc le taux d'évolution réciproque, il faut se le calculer à la main.Calcul du taux d'évolution réciproque
Ce qu'on va faire, c'est ça : on va d'abord calculer le coefficient multiplicateur qui nous permet de passer du prix initial au prix final. Ce coefficient multiplicateur, CM, il est facile à calculer. Quand j'ai moins 20% de taux d'augmentation, la formule est \(CM = 1 - \frac{t}{100}\), donc \(1 - \frac{20}{100} = 0.8\). Si vous ne savez pas comment faire pour calculer le coefficient multiplicateur, allez voir la petite vidéo qui s'affiche en haut et qui va vous le rappeler. Maintenant, on va calculer le coefficient multiplicateur réciproque, qu'on va appeler \(CM'\). C'est-à-dire le coefficient multiplicateur qui me permet de passer du prix final au prix initial. Ce coefficient multiplicateur, il est facile à calculer, c'est l'inverse du coefficient multiplicateur de la première direction, donc \(CM' = \frac{1}{0.8} = 1.25\). Maintenant que vous avez calculé le coefficient multiplicateur, vous allez pouvoir trouver le taux d'évolution réciproque en le calculant à partir du coefficient multiplicateur réciproque. Si j'ai un coefficient multiplicateur de 1.25, je sais que \(1.25 = 1 + t'\), donc \(t' = 0.25\). Donc, ma diminution est de 25%. Donc, si j'ai baissé le prix d'un pull de 20%, pour retrouver le prix initial, il ne faut pas augmenter de 20%, il faut augmenter de 25%. Nous avons mis des exercices en dessous. Notez les formules qui s'affichent, prenez-en note, faites les corrections, essayez de les faire. Je vous garantis que dans dix minutes de travail, vous maîtriserez ce truc là et vous n'oublierez jamais. À vous de jouer, vous êtes des champions.Nouvelle recrue
Visiteur anonyme
0 pts