Livre
2. Calculer des images et des antécédents
Conditions d'achèvement
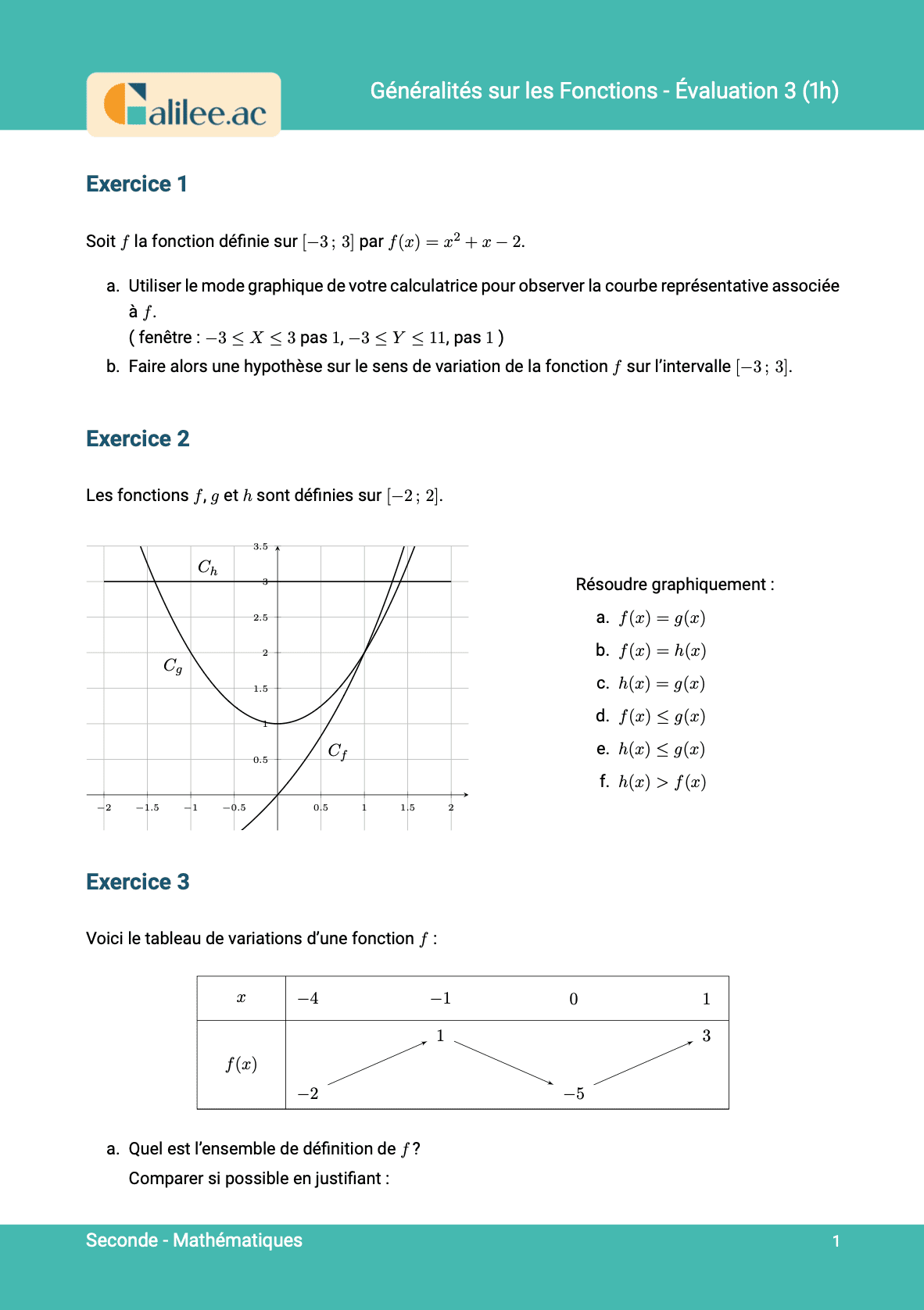
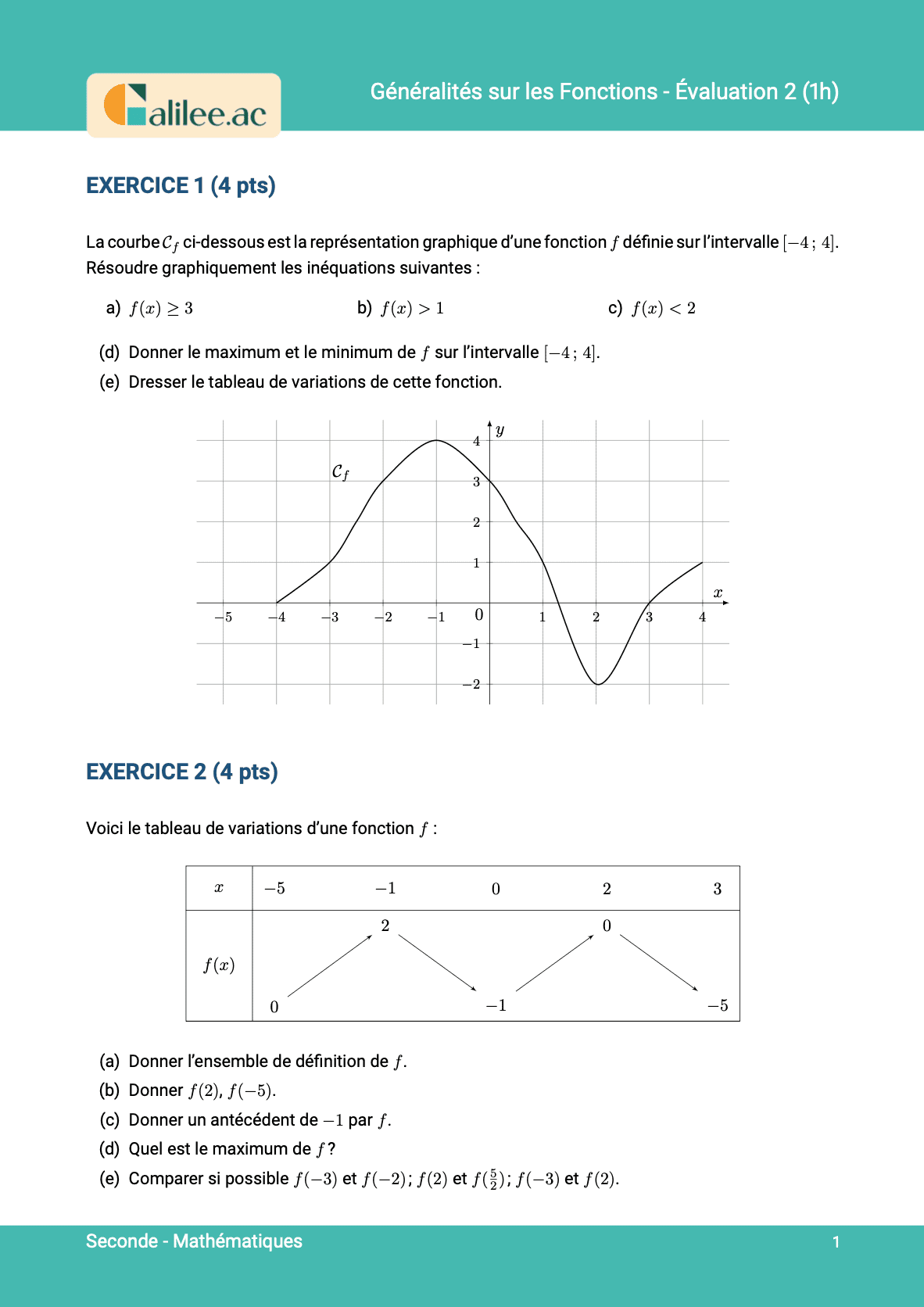
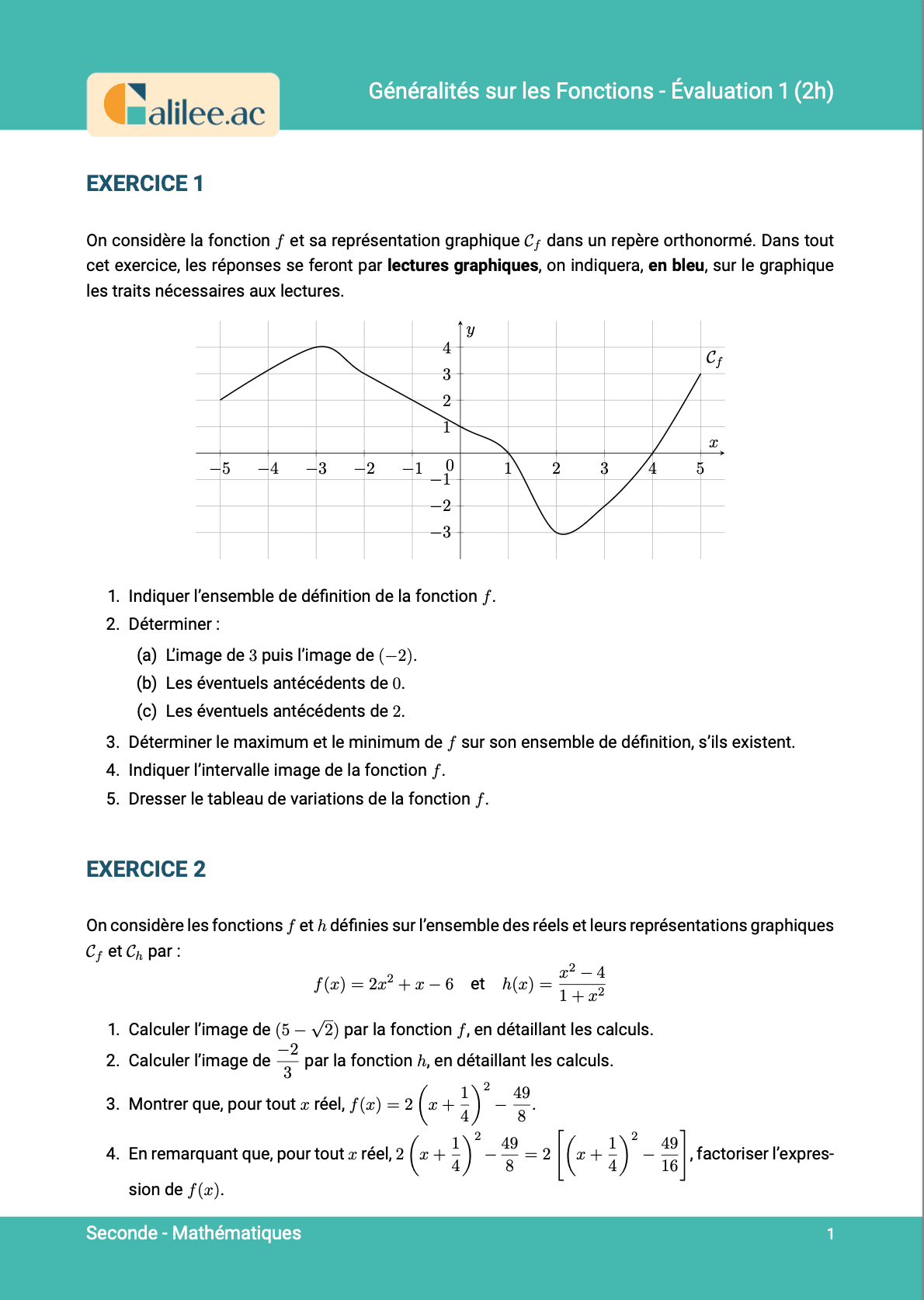
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Exercice
5
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Les familles ont des parties pour voir comment calculer très simplement des images et des antécédents quand on vous donne l'expression d'une fonction.Vocabulaire
Tout d'abord, un peu de vocabulaire. Quand vous lisez ou écrivez \(f(3) = 5\), cette phrase peut être interprétée de deux manières. Soit vous dites que l'image de 3 par la fonction \(f\) est 5, soit vous pouvez aussi dire que l'antécédent de 5 dans la fonction \(f\) est 3. Donc, soit je lis dans ce sens : l'image de 3 par \(f\) est 5, soit dans ce sens : l'antécédent de 5 par \(f\) est 3.Calcul de l'image
Du coup, quand je vous demande de calculer l'image de 3 par la fonction \(f\), tout ce que vous avez à faire c'est de calculer \(f(3)\). Or, vous savez que \(f(x)\) est \(2x - 5\). Donc, \(f(3)\) (l'image de 3) est \(2 \times 3 - 5\). On remplace le \(x\) qui était là par 3. Du coup, il n'y a pas de raison que je ne remplace pas le \(x\) par 3 aussi. \(2 \times 3 = 6\), \(6 - 5 = 1\). Ça me fait donc 1. L'image de 3 dans \(f\) est 1. L'image de 3 par \(f\) est 1.Calcul de l'antécédent
Maintenant, dans le sens où l'on cherche des antécédents, cette fois-ci, l'antécédent de 3 par \(f\), je ne le connais pas. Je l'appelle point d'interrogation. Mais par contre, je sais que ce point d'interrogation, quand je le mets dans \(f\), ça me fait 3. Donc ce point d'interrogation que je vais appeler \(x\), je sais que quand je le transforme par \(f\), ça donne 3. Or, on a vu que quand on transforme \(x\) par \(f\), ça fait \(2x - 5\). Donc, \(2x - 5 = 3\). Je me retrouve avec une équation à résoudre. Donc, pour mon \(-5\), je le passe de l'autre côté, ça devient \(+5\), et \(2x = 3 + 5 = 8\). Donc, \(x = 8 / 2\) parce que pour me débarrasser de ce 2, j'ai tout divisé par 2, et j'obtiens \(x = 4\). Du coup, l'antécédent de 3 par \(f\), c'est-à-dire le nombre \(x\) qui, quand je le mets dans ma fonction \(f\), donne 3, c'est \(x = 4\). Donc, l'antécédent de 3 par \(f\) est 4.Conclusion
Pour résumer, pour calculer l'image, vous avez juste à mettre ce nombre à la place de \(x\). Quand vous cherchez à calculer un antécédent, vous devez résoudre l'équation qui vous donne le nombre que vous cherchez. Une fois que ces histoires d'images et d'antécédents seront solidement acquises, vous allez voir que cette partie des mathématiques qui consiste à étudier des fonctions et qui s'appelle l'analyse, ça devient vraiment une partie de plaisir. Je vous assure que si ce vocabulaire est solide, jusqu'à la terminale, vous êtes plus ou moins tranquille, vous êtes des champions.Recrue
Visiteur anonyme
6 pts