Livre
14. Dresser le tableau de signe
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Exercice
5
Exercice
6
Pour aller plus loin : Contrôles sur ce chapitre 🎯
SecondeRecommandé
Devoir commun Fonctions, vecteurs et taux d'évolution - sujet 25
Chapitres: Étude de fonctions Vecteurs ...
SecondeRecommandé
Devoir commun Calcul, vecteurs et fonctions - sujet 36
Chapitres: Calculs numériques et littérals Vecteurs ...
SecondeRecommandé
Contrôle Généralités sur les fonctions - sujet 4
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Étude de fonctions et fonctions de référence - sujet 22
Chapitres: Étude de fonctions Fonctions de référence
SecondeRecommandé
Contrôle Inéquations et fonctions - sujet 9
Chapitres: Résolution d'inéquations Fonctions affines ...
SecondeRecommandé
Contrôle Généralités sur les Fonctions 1
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Fonctions et calcul numérique - sujet 10
Chapitres: Étude de fonctions Calculs numériques et littérals
SecondeRecommandé
Contrôle Généralités sur les fonctions - sujet 5
Chapitres: Étude de fonctions
SecondeRecommandé
Contrôle Nombres, repérage, fonctions et calcul - sujet 15
Chapitres: Ensembles de nombres Vecteurs ...
SecondeRecommandé
Contrôle Fonctions de référence et fonctions affines - sujet 13
Chapitres: Étude de fonctions Fonctions affines ...
SecondeRecommandé
Contrôle Fonctions et équations - sujet 8
Chapitres: Étude de fonctions Résolution d'équations
SecondeRecommandé
Contrôle Généralités sur les Fonctions 3
Chapitres: Étude de fonctions
je ne comprend pas
Introduction
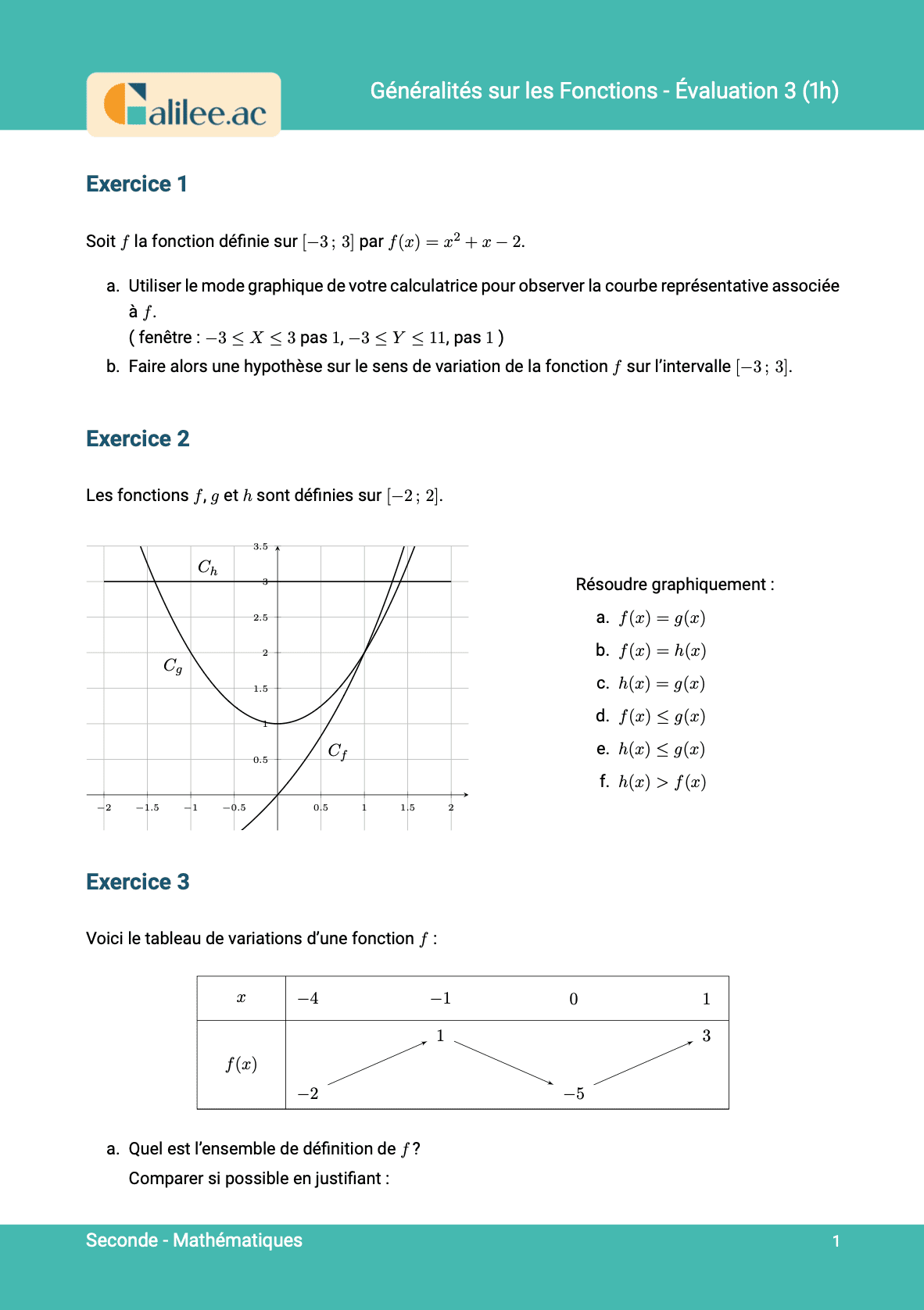
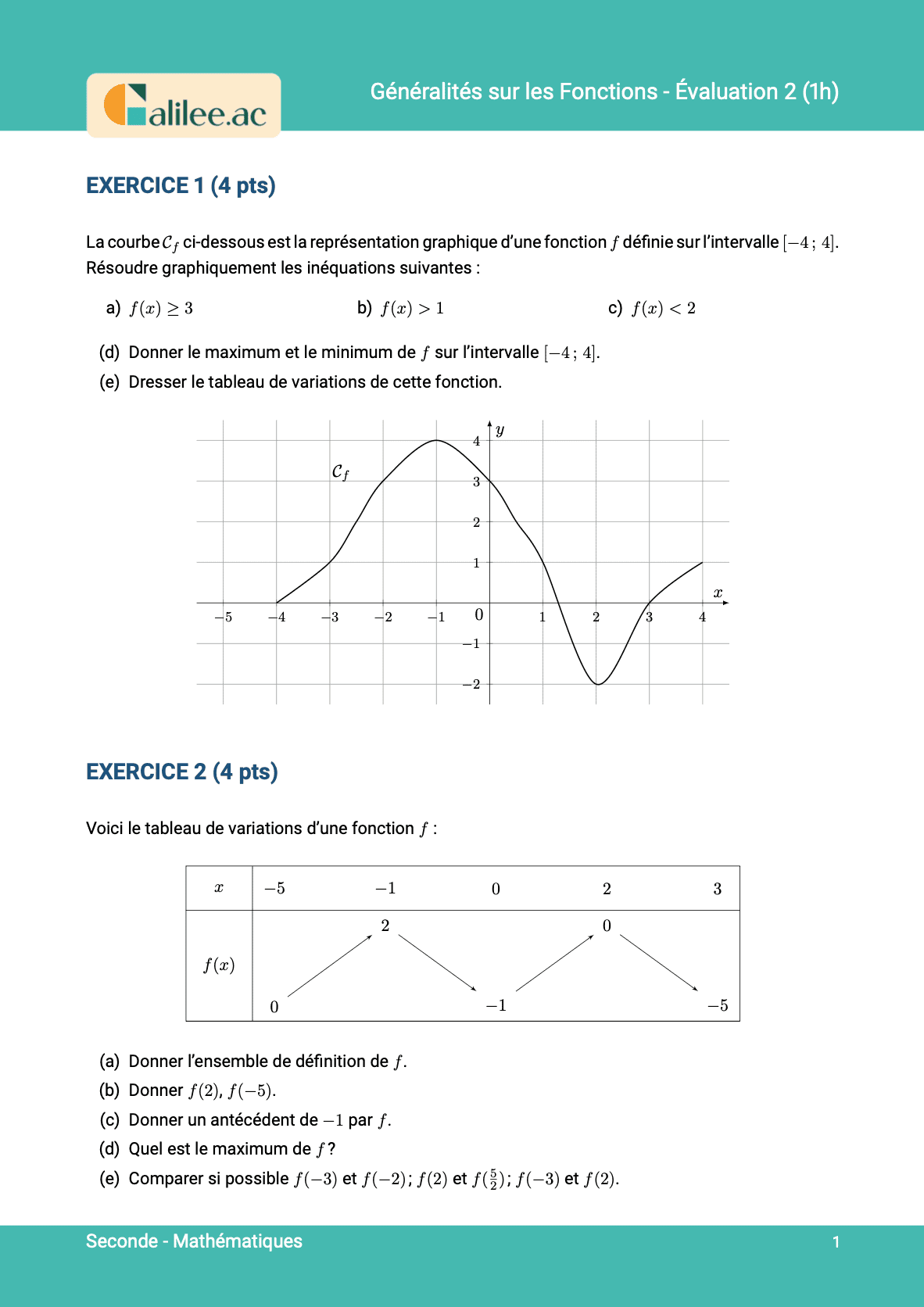
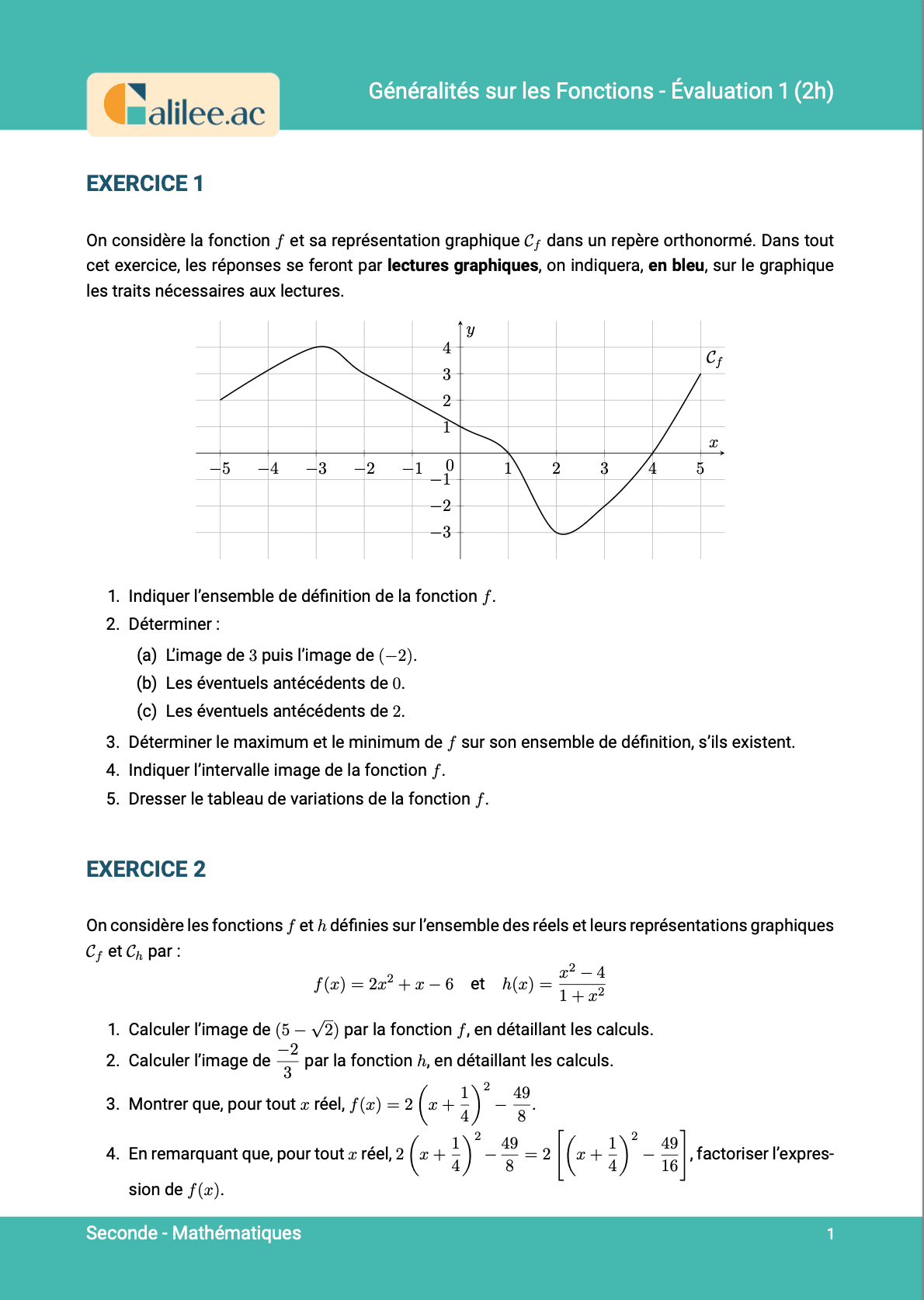
Allez les amis, on est parti pour voir une compétence que certains d'entre vous galèrent encore à faire : dresser le tableau de signes d'une fonction quand on vous donne la représentation graphique de cette fonction. Dresser le tableau de signes d'une fonction, c'est faire un tableau où on dira, en fonction des valeurs de \(x\) (c'est-à-dire en fonction des valeurs horizontales), si la fonction est positive ou négative.Comprendre le signe d'une fonction
Quand vous regardez cette fonction et que vous vous demandez si elle est positive, il y a deux manières de voir les choses. La première manière, qui de base sera compliquée, c'est de dire : "Je fixe \(y\), je suis dans les \(x\) positifs, donc ma fonction est positive ici". C'est une manière de voir les choses. La deuxième manière, c'est de dire : "Bon, je regarde les \(y\), ma fonction est positive quand elle est au-dessus du zéro, donc au-dessus de cette droite là". Donc elle est positive là, elle est positive là. Quelle est la bonne ? La bonne, c'est de se dire que les valeurs de la fonction, on ne les lit pas ici, on lit toujours là. Je vous rappelle que quand vous voulez faire l'image de 3, vous portez 2 à 3, vous descendez et vous allez lire la valeur sur l'axe vertical. Donc le signe d'une fonction, il se lit sur l'axe vertical et on se demande si la fonction est au-dessus de cette droite là qui passe par 0, c'est-à-dire que les valeurs positives sont au-dessus de cet axe.Exemple de tableau de signes
Donc cette fonction \(f\), on voit clairement qu'elle est positive là, jusqu'ici, et puis là, jusqu'ici. Comment est-ce qu'on va le représenter ? On va dire, c'est pas compliqué, en fonction des valeurs de \(x\), \(f(x)\) va avoir des signes différents. Donc moi, je sais que de -15 jusqu'à en gros -5,5, elle va être positive. Ensuite, de -5,5 à 8, elle va être négative. Puis, de 8 jusqu'à 15, elle va être positive. Entre temps, quand elle passe de positif à négatif, vous passez forcément par 0. Félicitations, vous venez de faire votre premier tableau de signes. Attention, la principale difficulté dans cette compétence, qui paraît très simple, c'est de se dire qu'une fonction est positive par rapport à l'axe horizontal, donc elle est au-dessus de cet axe là, puisque la valeur de la fonction, vous la lisez là-dessus. Les erreurs que je vois en cours, ce sont des élèves qui se disent : "Je regarde comme ça, et comme ça, les valeurs positives, c'est pas les \(x\) qui doivent être positifs, c'est \(f(x)\), donc l'image qu'on lit sur le vertical". On vous a mis des petits exercices en dessous, vous allez kiffer, c'est très simple. Faites-le, vous êtes des champions.Nouvelle recrue
Invité
0 pts
