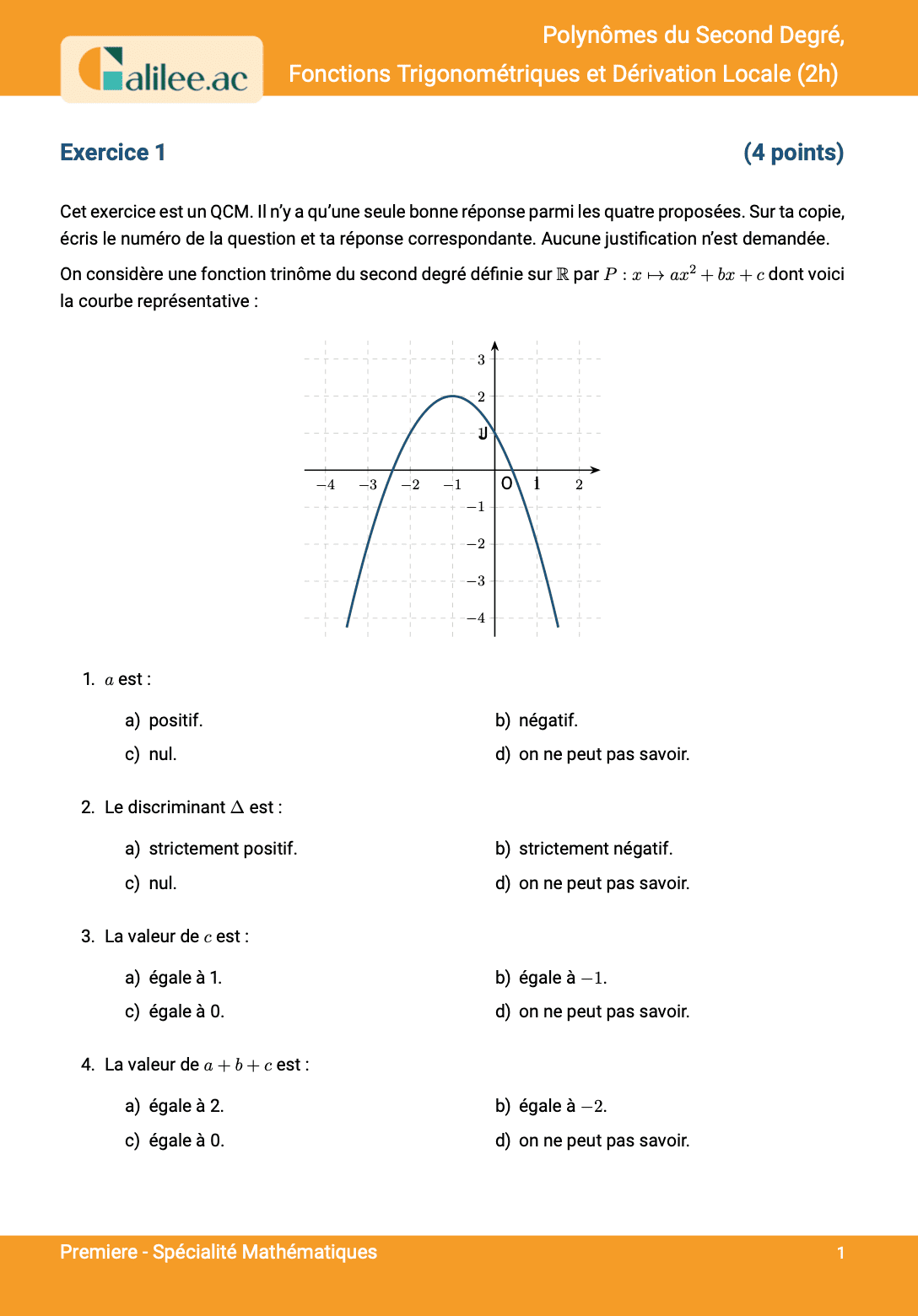
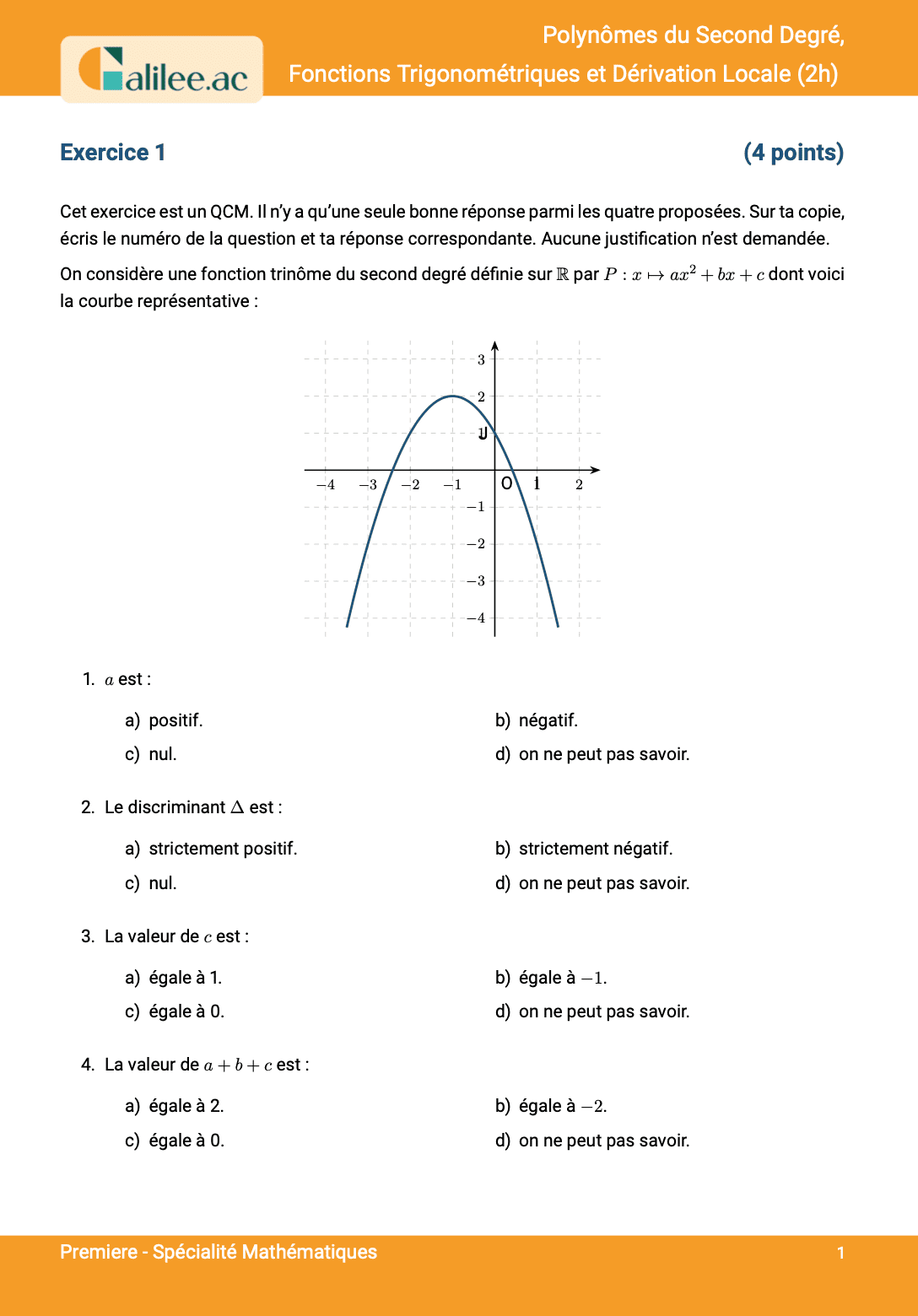
Livre
5. Donner tous les angles d'un point du cercle
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
3
Exercice
4
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Dans cette leçon, nous allons inverser ce que vous savez déjà faire. Jusqu'à présent, on vous a donné des valeurs d'angle, par exemple \(\frac{\pi}{4}\), et on vous a demandé de les positionner sur le cercle. Cette fois-ci, on va vous positionner des angles et on va vous demander de donner toutes les valeurs d'angle qui vous permettent d'arriver à ce point.Exemple avec \(\frac{\pi}{4}\)
Prenons l'exemple avec \(\frac{\pi}{4}\). Mon point de départ est toujours ici. Comment est-ce que je peux atteindre ce point en partant d'ici ? La première option est d'aller directement jusqu'à \(\frac{\pi}{4}\). Donc, je peux dire que le moyen le plus simple d'atteindre \(\frac{\pi}{4}\) est de faire \(\frac{\pi}{4}\). Cependant, je peux aussi atteindre ce point en faisant \(\frac{\pi}{4}\) plus un tour complet, c'est-à-dire \(\frac{\pi}{4} + 2\pi\). Je peux aussi l'atteindre en faisant \(\frac{\pi}{4}\) plus deux tours complets, soit \(\frac{\pi}{4} + 4\pi\), et ainsi de suite. Donc, tous les angles qui permettent d'atteindre \(\frac{\pi}{4}\) s'écrivent \(\frac{\pi}{4} + k\pi\), où \(k\) est un nombre entier qui indique combien de fois je dois faire le tour. Ce nombre peut être positif ou négatif. Pour le dire, on va dire que \(k\) appartient à \(Z\), c'est-à-dire que \(k\) peut prendre toutes les valeurs entières positives, toutes les valeurs entières négatives et aussi la valeur zéro.Exemple avec \(\frac{\pi}{2}\) et \(\frac{\pi}{3}\)
Si vous avez compris, alors passons à \(\frac{\pi}{2}\). Pour atteindre \(\frac{\pi}{2}\), je peux soit partir de 0 et suivre le sens des aiguilles d'une montre, soit je peux partir de 0, suivre \(\frac{\pi}{2}\) et faire un certain nombre de fois \(2\pi\), avec ce certain nombre étant un nombre entier. Pour \(\frac{\pi}{3}\), c'est exactement la même chose. Pour l'atteindre, je vais faire \(\frac{\pi}{3} + k\pi\), avec \(k\) appartenant à \(Z\).Conclusion
Si on vous demande de trouver les angles qui correspondent à un point sur un certain intervalle, vous commencez par trouver toutes les valeurs possibles, puis vous regardez, en fonction des valeurs de \(k\), quelles valeurs restent dans l'intervalle que vous recherchez.Soldat
Visiteur anonyme
15 pts