Livre
4. Représentation graphique d'une suite récurrente
Conditions d'achèvement
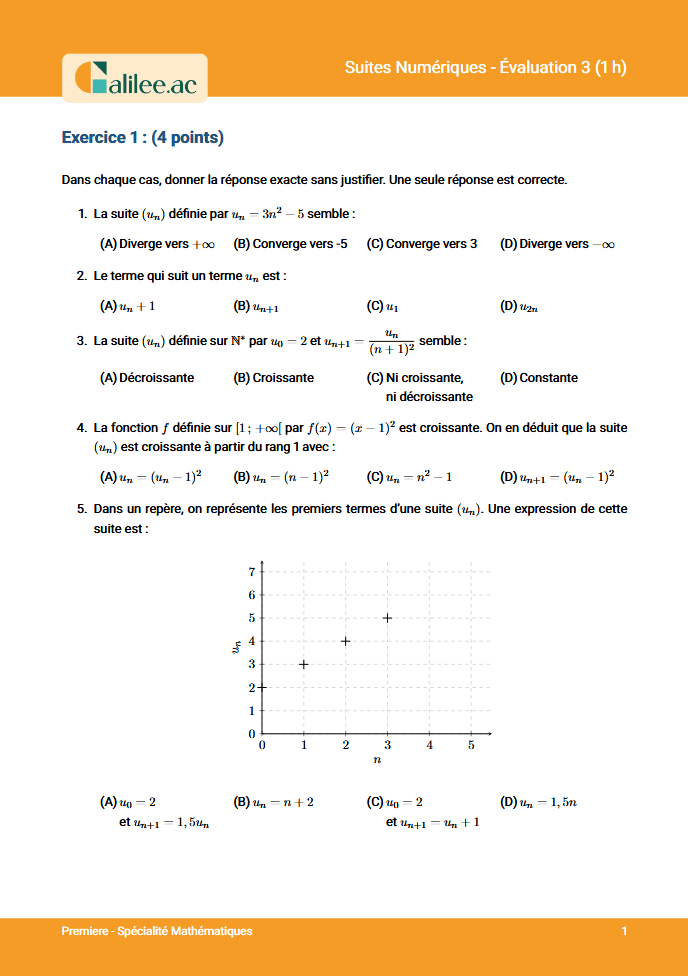
Exercice
1
Exercice
2
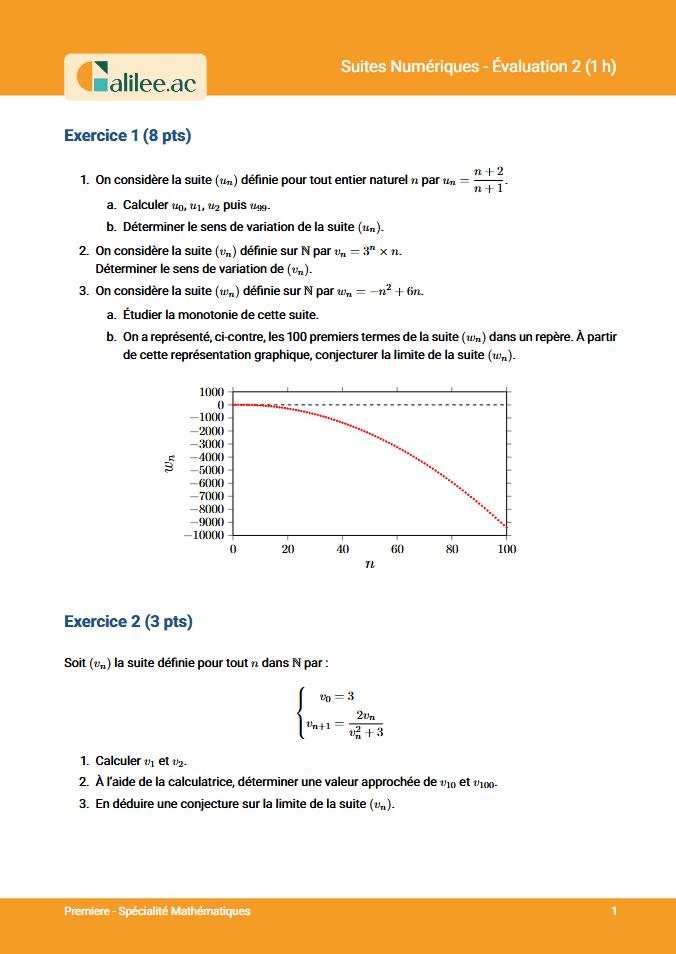
Exercice
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Alors, nous allons parler des représentations de suites. Cependant, cela va être un peu plus compliqué qu'avec les suites définies de manière explicite. Prenons par exemple la suite \(u_n\) où \(u_{n+1} = f(u_n)\) et \(u_0 = 3\). Qu'est-ce que cela signifie ? Cela signifie que pour obtenir le terme suivant, nous prenons le terme précédent et le transformons grâce à la fonction \(f\). Nous allons donc nous servir de la représentation graphique de la fonction \(f\) pour transformer les termes et pouvoir calculer les termes suivants.Représentation graphique de la suite
Nous commençons avec \(u_0 = 3\). Nous positionnons \(u_0\) à 3 sur l'axe des ordonnées. Pour obtenir le terme suivant, c'est-à-dire \(u_1\), nous devons transformer \(u_0\) avec la fonction \(f\). Nous prenons donc \(u_0\), montons jusqu'à la fonction \(f\) et lisons \(u_1\) sur l'axe des ordonnées. Cependant, pour calculer \(u_2\), nous devons prendre \(u_1\) et le transformer avec la fonction \(f\). Or, si \(u_1\) est sur l'axe des ordonnées, nous ne pouvons pas le transformer avec la fonction \(f\) car pour transformer un nombre avec une fonction, il faut qu'il soit sur l'axe des abscisses. Pour résoudre ce problème, nous allons utiliser la droite \(y = x\) qui nous permet de prendre \(u_1\) et de le repositionner sur l'axe des abscisses. Nous allons donc monter jusqu'à la droite \(y = x\) et redescendre pour obtenir \(u_1\) sur l'axe des abscisses.Calcul des termes suivants de la suite
Pour calculer le terme suivant, c'est-à-dire \(u_2\), nous devons prendre le terme précédent, c'est-à-dire \(u_1\), et le transformer à travers la fonction \(f\). Nous prenons donc \(u_1\), montons jusqu'à la fonction \(f\) et lisons \(u_2\) sur l'axe des ordonnées. Ensuite, nous prenons \(u_2\) et le repositionnons sur l'axe des abscisses grâce à la droite \(y = x\). Nous pouvons répéter ce processus pour calculer les termes suivants de la suite. Au fur et à mesure que nous calculons les termes de la suite, nous nous rendons compte que nous faisons des allers-retours entre l'axe des ordonnées et l'axe des abscisses. Cela nous donne une idée de la limite de la suite. En effet, à partir d'un certain point, la suite semble se stabiliser autour d'une certaine valeur. Dans notre exemple, il semble que la suite \(u_n\) ait pour limite 8.5. Pour mieux comprendre ce concept, je vous recommande de faire les exercices qui sont en dessous. Cela vaut le coup de faire des dessins et de se familiariser avec cette méthode de construction pour arriver à reproduire la même chose. C'est un type d'exercice qui tombe souvent au contrôle. Alors, à vous de jouer !Nouvelle recrue
Visiteur anonyme
0 pts