Livre
12. Algorithme qui calcule les sommes de termes d'une suite
Conditions d'achèvement
Exercice
1
Exercice
2
Exercice
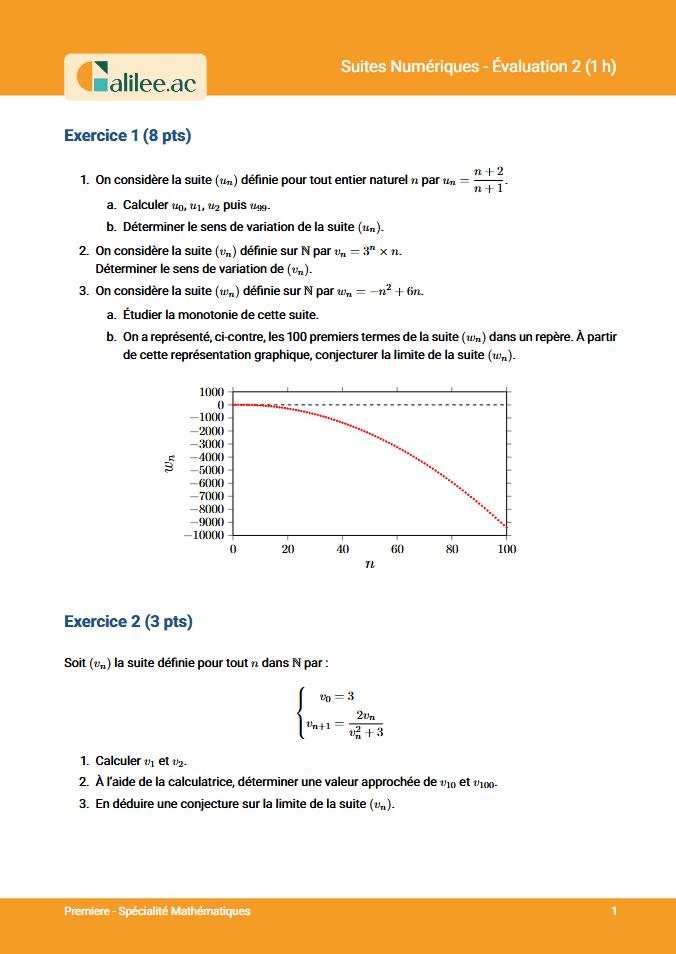
3
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Introduction
Allez les copains, c'est parti pour un feu d'algorithmes, dans une version légèrement plus difficile que ce qu'on a fait avant. Cette fois-ci, on ne va pas se contenter de faire un algorithme qui donne par exemple le quatrième terme d'une suite. On va faire un algorithme qui donne la somme des quatre premiers termes de la suite. Donc, \(u_n = u_{n-1} + 3n + 2\). Concentrez-vous, ça va piquer.Explication de l'algorithme
On fait l'algorithme suivant. C'est vraiment un cas classique. Si vous avez bien vu la vidéo d'avant, vous reconnaissez que ces deux choses sont importantes : \(v = 3\) et \(v = 3n + 2\). Donc, vous vous dites, ce n'est pas compliqué, je vais le suivre. On a \(v_n = 3v_{n-1} + 2\) et j'ai un premier terme \(v_0\) qui vaut 3. Donc, cet algorithme va le faire de 1 jusqu'à 7. Attention, en Python, quand vous faites un range, il va commencer à 1 mais il ne va pas aller jusqu'à 7, il va le faire jusqu'à 6. Il évite toujours la dernière valeur que vous mettez. Donc, si vous mettez par exemple 10, il va aller de 0 jusqu'à 9. Donc, il va faire six fois l'opération de répéter ce truc là. Donc, ce qu'on va avoir, c'est le septième terme de la suite. Ça, ce n'est pas compliqué.Calcul de la somme des termes de la suite
Maintenant, la question qu'on se pose, c'est comment faire pour qu'il calcule la somme des sept premiers termes, c'est-à-dire \(v_0 + v_1 + v_2 + \ldots + v_6\), le septième terme de la suite \(v\). Pour cette question, le seul moyen de la traiter, c'est de se dire, bon, j'ai mon petit papier, un petit papier qui s'appelle \(v\) et dans lequel je vais mettre à chaque fois la valeur de ma suite. Ce petit papier ne va pas être suffisant pour servir de réservoir pour stocker les valeurs, parce que ce petit papier, à chaque fois, on est obligé de l'effacer. Donc, on ne peut pas s'en sortir avec ce petit papier. Par contre, imaginez qu'on a un autre papier à côté qu'on appelle par exemple \(s\), et que sur ce papier, chaque fois qu'on a calculé une nouvelle valeur de \(v\), on dit, ce n'est pas compliqué, pour avoir une nouvelle valeur de \(s\), je prends ce que j'avais avant et je rajoute ce que je viens de trouver. De cette manière, je garde toujours mon stock et chaque fois que je calcule une nouvelle valeur de \(v\), je la rajoute à \(s\). Cette variable va nous servir de variable de stockage. Donc, on la définit ici, \(s\), elle commence vide. Chaque fois que j'ai calculé une nouvelle valeur de \(v\), ma variable \(s\) est mise à jour. La nouvelle valeur de \(s\) va être l'ancienne, donc ce que j'ai stocké jusqu'à présent, plus ce que je viens de calculer. Et à la fin, je ne vais pas retourner \(v\), parce que ce n'est pas ça qui m'intéresse, je retourne \(s\). Ce truc là, \(s = s + v\), retenez-le, franchement, retenez-le, ça coûte pas cher, c'est tout simple, \(s = s + v\), et ça vous permet vraiment de gagner des points pendant les contrôles, parce que ça, ce sont des questions qui tombent souvent. Allez, on va maintenant regarder quelques exemples en dessous.Nouvelle recrue
Visiteur anonyme
0 pts