Livre
7. Équation d'une tangente par le calcul
Conditions d'achèvement
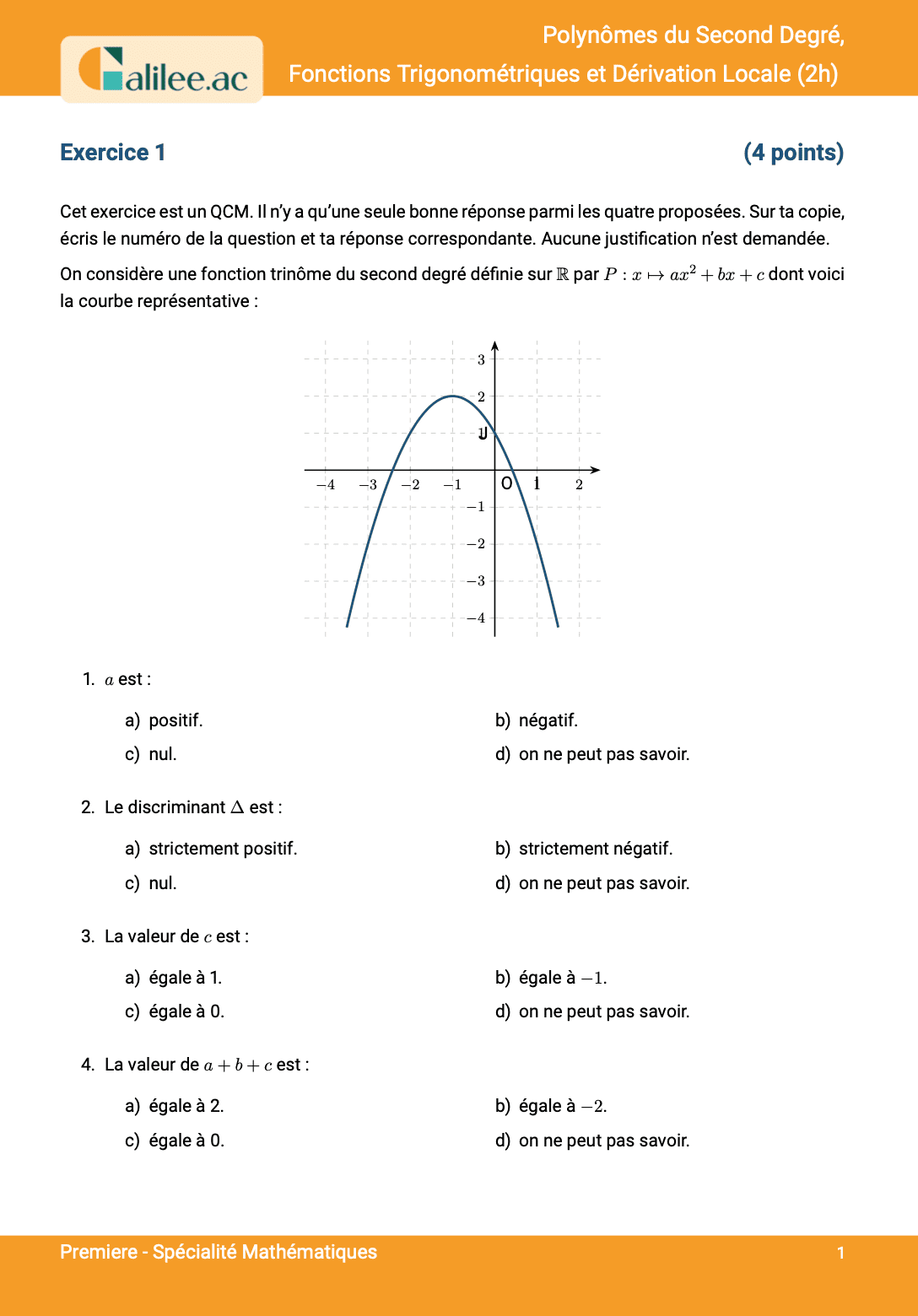
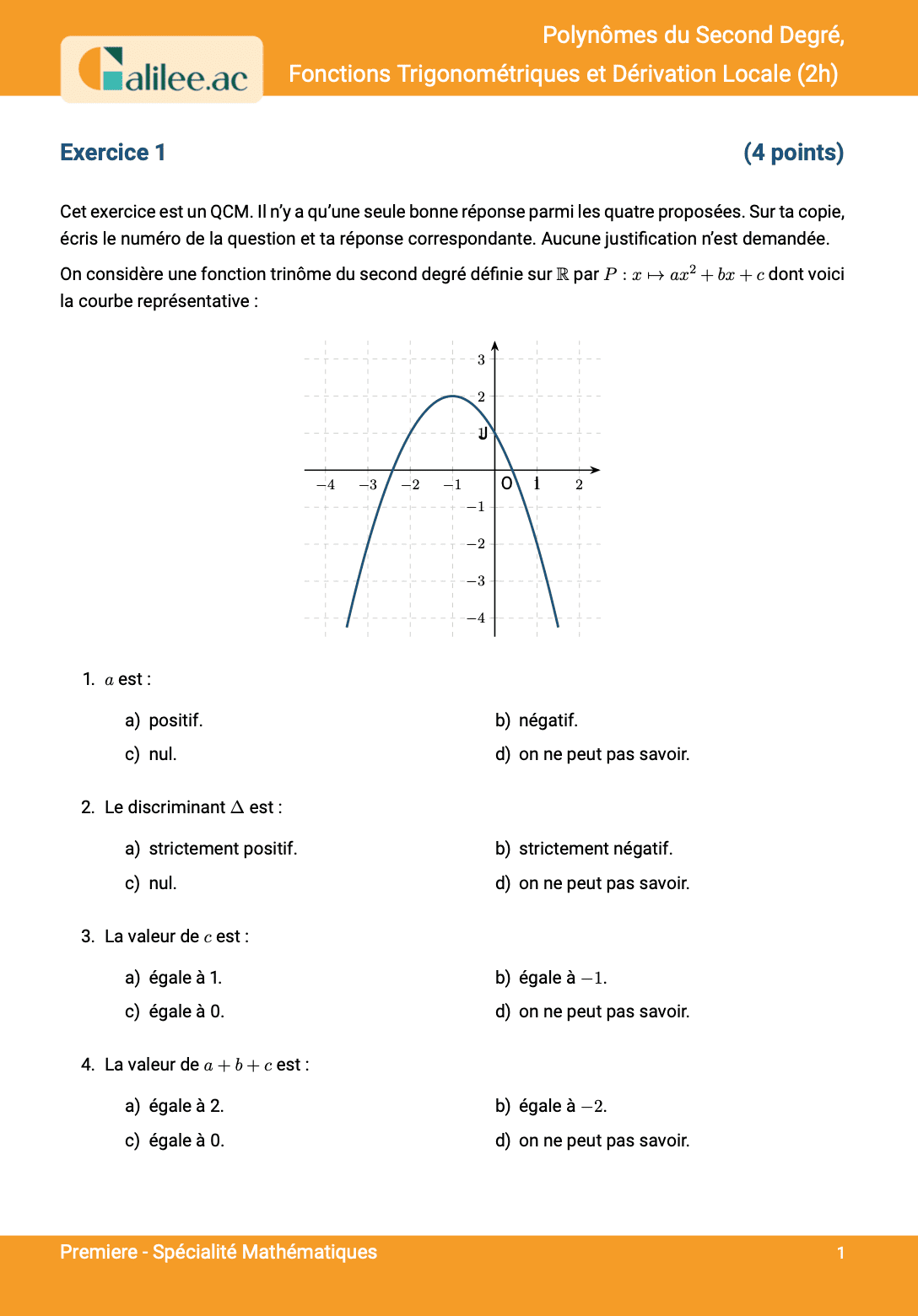
Exercice
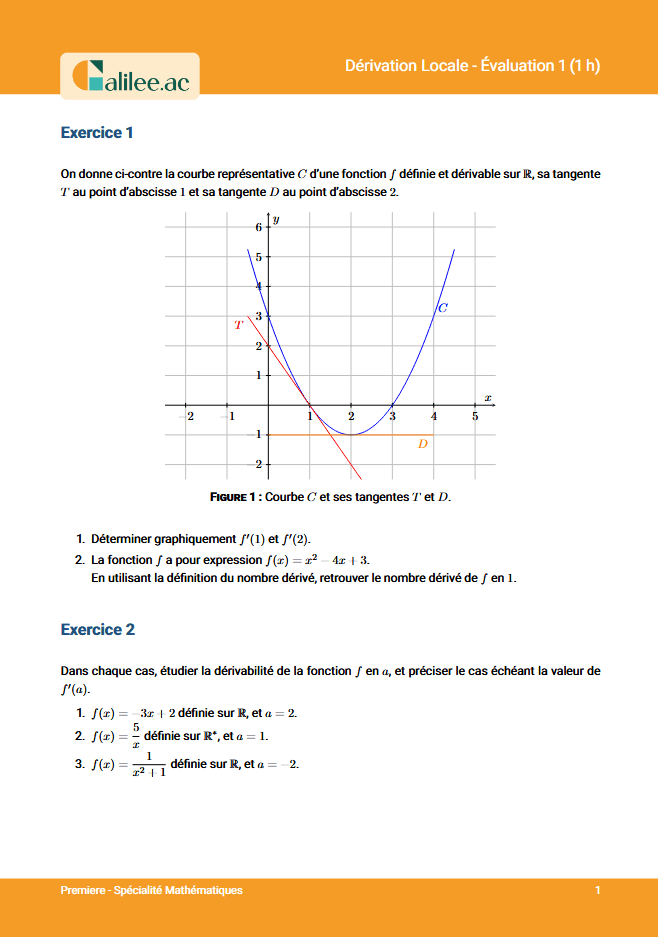
1
Exercice
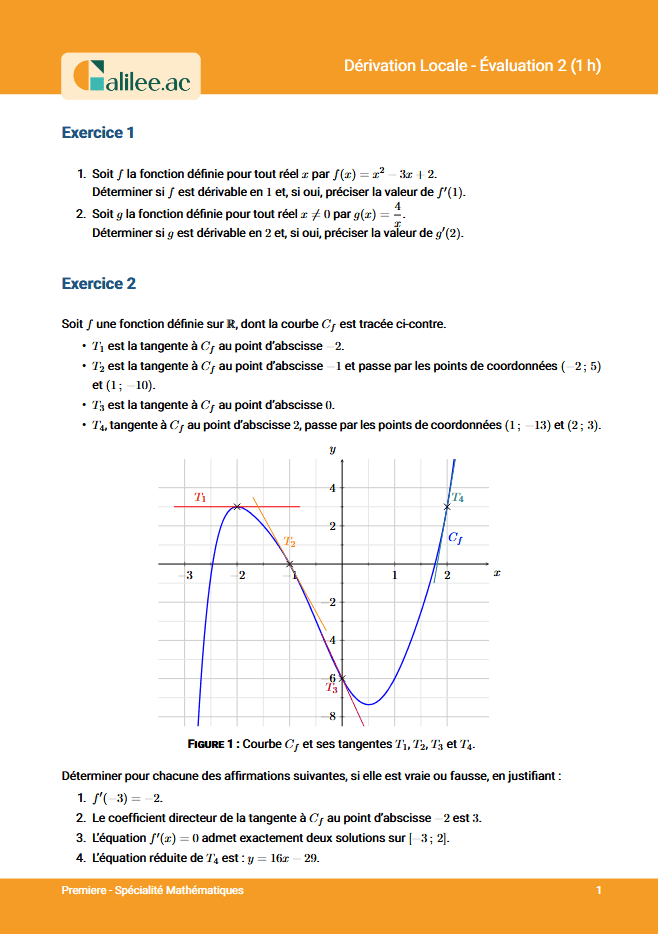
2
Pour aller plus loin : Contrôles sur ce chapitre 🎯
Première spécialitéRecommandé
Contrôle Automatismes, Dérivation Locale et Proba Conditionnelles
Chapitres: Automatismes Dérivation locale ...
Première spécialitéRecommandé
Contrôle Second Degré, Fonctions Trigo et Dérivation Locale
Chapitres: Polynômes du second degré Trigonométrie ...
PremièreRecommandé
Contrôle Dérivation Locale 1
Chapitres: Dérivation locale
PremièreRecommandé
Contrôle Second Degré Trigo Derivation Locale
Chapitres: Polynômes du second degré Trigonométrie ...
PremièreRecommandé
Contrôle Dérivation Locale 2
Chapitres: Dérivation locale
Bonjour @Atelier SophieRio
Cela te permet de connaitre les diverses manière d'opérer !!
Cela te permet de connaitre les diverses manière d'opérer !!
Bonjour,
J’aimerais savoir pourquoi dans les exercices vous faites toujours tendre la limite vers le point d’abscisse donné dans l’énoncé, tandis que dans la vidéo de cours vous faites tendre la limite vers 0 alors que le point d’abscisse donné est 1.
Merci,
J’aimerais savoir pourquoi dans les exercices vous faites toujours tendre la limite vers le point d’abscisse donné dans l’énoncé, tandis que dans la vidéo de cours vous faites tendre la limite vers 0 alors que le point d’abscisse donné est 1.
Merci,
Bonjour ! est ce que c'est normal que je peux faire les exercices mais que je ne peux pas voir le corrigé? c'est dommage quand même
je pense que vous vous etes trompez dans l'exercice 1 puisque f(-4+h) est egale à -2/(-4+h)+5, pouvez vous m'expliquez l'exercice 1 s'il vous plait
Bonjour @juliealfred
Il n'y a pas de f(-4+h) dans l'exercice 1 après notre vérification !
Peux-tu être un peu plus précise ?
Il n'y a pas de f(-4+h) dans l'exercice 1 après notre vérification !
Peux-tu être un peu plus précise ?
Bonjour,
Je ne suis pas sûr de saisir la différence entre le coefficient directeur / taux de variation et l’équation de la tangente ? J’ai l’impression que ça représente la même chose et qu’il y a différents formules. J’ai peur de m’emmêler les pinceaux.
Merci d’avance !
Je ne suis pas sûr de saisir la différence entre le coefficient directeur / taux de variation et l’équation de la tangente ? J’ai l’impression que ça représente la même chose et qu’il y a différents formules. J’ai peur de m’emmêler les pinceaux.
Merci d’avance !
👍
Introduction
Déterminons l'équation réduite de la tangente au point d'abscisse. Dans cet exercice, nous n'avons pas la représentation graphique de la fonction, donc nous allons utiliser la formule suivante pour calculer l'équation réduite d'une tangente : \(y = f'(a)(x - a) + f(a)\). Ce qui va nous intéresser dans cet exercice, c'est de calculer \(f'(a)\) et \(f(a)\) au point d'abscisse \(a\).Calcul de la dérivée
Pour calculer la dérivée, si nous avions la représentation graphique de la fonction, nous aurions utilisé la définition graphique de la dérivée, c'est-à-dire que la dérivée est le coefficient directeur de la tangente. Mais ici, nous n'avons pas la représentation graphique, donc nous allons devoir passer par la technique qui consiste à calculer la dérivée à partir de la limite du taux de variation. Pour cela, nous allons d'abord calculer \(f(a + h)\), puis \(f'(a)\), et enfin \(f(a + h) - f(a) / h\). Par exemple, si \(f(x) = 3 / (x + 1)\), alors \(f(a + h) = 3 / (a + h + 1)\) et \(f(a) = 3 / (a + 1)\). Ensuite, nous calculons \(f(a + h) - f(a) / h = (3 / (a + h + 1) - 3 / (a + 1)) / h\). Pour simplifier cette expression, nous mettons tout au même dénominateur, ce qui donne \((3(a + 1) - 3(a + h + 1)) / ((a + h + 1)(a + 1)h)\). En simplifiant, nous obtenons \(-3h / ((a + h + 1)(a + 1)h)\), qui se simplifie en \(-3 / (a + h + 1)(a + 1)\). Enfin, nous calculons la limite de cette expression lorsque \(h\) tend vers 0, ce qui donne \(-3 / (a + 1)^2\). C'est donc la dérivée de la fonction au point \(a\).Calcul de la valeur de la fonction
Pour calculer la valeur de la fonction au point \(a\), nous remplaçons simplement \(x\) par \(a\) dans l'expression de la fonction. Par exemple, si \(f(x) = 3 / (x + 1)\), alors \(f(a) = 3 / (a + 1)\).Équation de la tangente
Une fois que nous avons calculé la dérivée et la valeur de la fonction au point \(a\), nous pouvons utiliser la formule de l'équation de la tangente pour obtenir l'équation de la tangente au point \(a\). Par exemple, si \(f'(a) = -3 / (a + 1)^2\) et \(f(a) = 3 / (a + 1)\), alors l'équation de la tangente est \(y = -3 / (a + 1)^2 (x - a) + 3 / (a + 1)\). En conclusion, lorsque nous voulons calculer l'équation de la tangente et que nous n'avons pas la représentation graphique, nous passons par le calcul de la dérivée à partir du taux de variation et de la limite, puis nous calculons la valeur de la fonction au point d'abscisse, et enfin nous utilisons la formule de l'équation de la tangente.Nouvelle recrue
Invité
0 pts
Je voulais savoir pourquoi vous n'utilisez pas le même chemin que la vidéo pour trouver f'(x). Dans la vidéo on calcule le taux de variation avec h et ensuite on calcule la limite pour trouver f'(x) mais ce n'est pas la même chose dans l'exercice 1.